《数据挖掘导论》Pangaea-Ning Tan 读书笔记 ----第五章 分类其他技术
文章目录
- 第五章 分类:其他技术
- 5.1 基于规则的分类
- 5.1.1 基于规则的分类器的工作原理
- 5.1.2 规则的排序方案
- 5.2 最近邻算法(KNN)
- 无监督最近邻
- KDTree和BallTree类
- 最邻近算法分类
- 最近邻回归
- 5.3贝叶斯分类器
- 5.3.1 贝叶斯定理
- 5.3.2 贝叶斯定理在分类中的应用
- 5.3.3 朴素贝叶斯分类器
- 5.3.4 贝叶斯误差率
- 5.3.5贝叶斯信念网络
- 5.3.6 贝叶斯模型代码实现
- 5.4人工神经网络
- 5.5支持向量机(SVM)
- 5.5.1 最大边缘超平面
- 5.5.2 线性支持向量机:可分情况
- 5.5.3 线性支持向量机:不可分情况
- 5.5.4 非线性支持向量机
- 5.6 组合方法
- 5.6.1组合方法的基本原理(略)
- 5.6.2构建组合分类器的方法
- 5.6.3 偏倚-方差分解
- 5.6.4 装袋
- 5.6.5 提升(boosting)
- 5.6.6 随机森林
- 5.7 不平衡类的问题
- 5.7.1 可选度量
- 5.7.2 接收者操作特征曲线(ROC)
- 5.7.3 代价敏感学习
- 5.7.4 基于抽样的方法
- 5.8 多类问题
第五章 分类:其他技术
5.1 基于规则的分类
基于规则的分类和决策树感觉是一样的,相当于把决策树又理论化了。。。
定义1:规则
每一分类规则可以表示为如下规则形式:
r i : ( 条 件 ) − > y i r_i:(条件)->y_i ri:(条件)−>yi
规则左边为规则前件或者前提,是属性测试的并集:
条 件 i = ( A 1 o p v 1 ) ∧ ( A 2 o p v 2 ) ∧ . . . ∧ ( A k o p v k ) 条件_i = (A_1 \ op \ v_1) \wedge (A_2 \ op \ v_2) \wedge ...\wedge (A_k \ op \ v_k) 条件i=(A1 op v1)∧(A2 op v2)∧...∧(Ak op vk)
其中 ( A j , v j ) (A_j,v_j) (Aj,vj)是属性——值对,op是比较运算符。每一个 ( A j o p v j ) (A_j \ op \ v_j) (Aj op vj)称为合取项。规则的右边称为规则后性,包含预测类 y i y_i yi
定义2 覆盖率 准确率
分类规则的质量可以用覆盖率和准确率来度量,给定数据集D和分类规则 r : A − > y r:A->y r:A−>y, 规则的覆盖率定义为D中的出发规则r的记录所占的比例。另一方面,准确率或置信因子定义为出发r的记录中类标号等于y 的记录所占的比例。
C o v e r a g e ( r ) = ∣ A ∣ ∣ D ∣ A c c u r a c y ( r ) = ∣ A ∩ y ∣ ∣ A ∣ Coverage(r)=\frac{|A|}{|D|} {}\\ {}\\ Accuracy(r)=\frac{|A \cap y|}{|A|} Coverage(r)=∣D∣∣A∣Accuracy(r)=∣A∣∣A∩y∣
5.1.1 基于规则的分类器的工作原理
常见的基于的规则:
- 互斥规则
- 穷举规则
- 有序规则
- 无序规则
5.1.2 规则的排序方案
基于规则的排序方案
基于类的排序方案
C4.5 ,RIPPER
5.2 最近邻算法(KNN)
最近邻分类器是一种非参数分类器,只是通过去寻找样本点周围的K个点,然后通过投票选出类标签最多的一类作为样本点的一类,所以直接进行实例:
无监督最近邻
from sklearn.neighbors import NearestNeighbors
import numpy as np
X = np.array([[-1,-1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]]) # 构建数组
# 分类器初始化
nbrs = NearestNeighbors(n_neighbors=2,algorithm='ball_tree')
# 训练数据
nbrs.fit(X)
# 返回训练结果
distances,indices=nbrs.kneighbors(X)
>>>indices # 对应位置上点所对应分的类,通过聚类样本一共分为了5类,indices按照索引顺序输出类别。
array([[0, 1],
[1, 0],
[2, 1],
[3, 4],
[4, 3],
[5, 4]], dtype=int64)
>>>distances #
array([[0. , 1. ],
[0. , 1. ],
[0. , 1.41421356],
[0. , 1. ],
[0. , 1. ],
[0. , 1.41421356]])
>>>nbrs.kneighbors_graph(X).toarray() # 通过稀疏点描述各个点之间的距离
array([[1., 1., 0., 0., 0., 0.],
[1., 1., 0., 0., 0., 0.],
[0., 1., 1., 0., 0., 0.],
[0., 0., 0., 1., 1., 0.],
[0., 0., 0., 1., 1., 0.],
[0., 0., 0., 0., 1., 1.]])
KDTree和BallTree类
我们可以单独通过KDTree和BallTree类来进行聚类
from sklearn.neighbors import KDTree
X = np.array([[-1,-1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]])
kdt = KDTree(X,leaf_size=30,metric='euclidean')
kdt.query(X,k=2,return_distance=False)
array([[0, 1],
[1, 0],
[2, 1],
[3, 4],
[4, 3],
[5, 4]], dtype=int64)
最邻近算法分类
在sklearn中有两种基于最邻近思想的分类,
-
一种是基于K(个数):KNeighborsClassifier,
-
一种基于r(半径): RadiusNeighborsClassifier
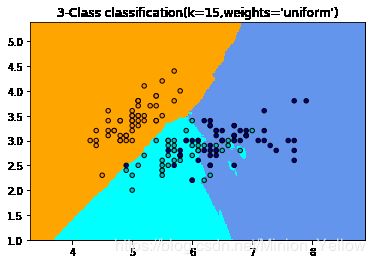
通过鸢尾花案例,来学习最近邻算法。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors,datasets
%matplotlib inline
n_neighbors = 15
iris = datasets.load_iris()
# 方便计算,只使用鸢尾花的两个特征
X = iris.data[:,:2]
y = iris.target
h = .02 # step size in the mesh
# create color maps
cmap_light = ListedColormap(['orange','cyan','cornflowerblue'])
cmap_bold = ListedColormap(['darkorange','c','darkblue'])
for weights in ['uniform','distance']:
# we create an instace of Neighbours Classifier and fit the data.
clf = neighbors.KNeighborsClassifier(n_neighbors,weights=weights)
clf.fit(X,y)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min,x_max]x[y_min,y_max]
x_min,x_max = X[:,0].min() - 1,X[:,0].max()+1
y_min,y_max = X[:,1].min() - 1,X[:,1].max()+1
xx,yy = np.meshgrid(np.arange(x_min,x_max,h),
np.arange(y_min,y_max,h))
Z = clf.predict(np.c_[xx.ravel(),yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx,yy,Z,cmap=cmap_light)
# Plot also the training points
plt.scatter(X[:,0],X[:,1],c=y,cmap=cmap_bold
,edgecolor = 'k',s=20)
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title("3-Class classification(k=%i,weights='%s')"%(n_neighbors,weights))
plt.show()
最近邻回归
SKlearn有两种不同的最近邻回归:
-
基于K: KNeighborsRegressor
-
基于R: RadiusNeighborsRegressor
都具有共同的属性: weights
weights:参数
- 1.uniform : 默认所有的点具有一样的权重
- 2.distance: 权重和距离之间呈反比
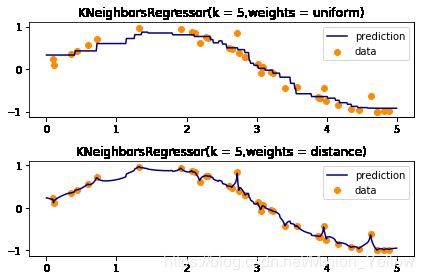
示例1 使用最近邻进行回归
import numpy as np
import matplotlib.pyplot as plt
from sklearn import neighbors
%matplotlib inline
np.random.seed(0)
X = np.sort(5*np.random.rand(40,1),axis=0)
T = np.linspace(0,5,500)[:,np.newaxis]
y = np.sin(X).ravel()
# Add noise to targets
y[::5] += 1*(0.5 - np.random.rand(8))
# create model
n_neighbors = 5
for i,weights in enumerate(['uniform','distance']):
knn = neighbors.KNeighborsRegressor(n_neighbors,weights=weights)
y_ = knn.fit(X,y).predict(T)
plt.subplot(2,1,i+1)
plt.scatter(X,y,color='darkorange',label='data')
plt.plot(T,y_,color='navy',label='prediction')
plt.axis('tight')
plt.legend()
plt.title("KNeighborsRegressor(k = %i,weights = %s)"%(n_neighbors,weights))
plt.tight_layout()
plt.show()
示例2 进行多输出回归案例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_olivetti_faces
from sklearn.utils.validation import check_random_state
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import RidgeCV
%matplotlib inline
# Load the faces datasets
Tdata= fetch_olivetti_faces()
data = Tdata.data
target = Tdata.target
train = data[target < 30]
test = data[target >= 30] # Test on indepent people
# Test on a subset of people
n_faces = 5
rng = check_random_state(4)
face_ids = rng.randint(test.shape[0],size=(n_faces,))
test = test[face_ids,:]
n_pixels = data.shape[1]
# Upper half of the faces
X_train = train[:,:(n_pixels+1)//2]
#Lower half of the faces
y_train = train[:,n_pixels//2:]
X_test = test[:,:(n_pixels + 1)//2]
y_test = test[:,n_pixels//2:]
# Fit estimators
ESTIMATORS={
"Extra trees" : ExtraTreesRegressor(n_estimators=10,max_features=32,random_state=0)
,"K-nn":KNeighborsRegressor()
,"Linear regression":LinearRegression()
,"Ridge":RidgeCV()
}
y_test_predict = dict()
for name,estimator in ESTIMATORS.items():
estimator.fit(X_train,y_train)
y_test_predict[name]=estimator.predict(X_test)
# Plot the completed faces
image_shape = (64,64)
n_cols = 1+len(ESTIMATORS)
plt.figure(figsize = (2. * n_cols, 2.26 * n_faces))
plt.suptitle("Face completion with multi-output estimators",size=16)
for i in range(n_faces):
true_face = np.hstack((X_test[i],y_test[i]))
if i :
sub = plt.subplot(n_faces,n_cols,i*n_cols+1)
else:
sub = plt.subplot(n_faces,n_cols,i*n_cols+1,
title = "true faces")
sub.axis("off")
sub.imshow(true_face.reshape(image_shape)
,cmap=plt.cm.gray
,interpolation="nearest")
for j,est in enumerate(sorted(ESTIMATORS)):
completed_face = np.hstack((X_test[i],y_test_predict[est][i]))
if i :
sub = plt.subplot(n_faces,n_cols,i*n_cols+2+j)
else:
sub = plt.subplot(n_faces,n_cols,i*n_cols+2+j
,title=est)
sub.axis("off")
sub.imshow(completed_face.reshape(image_shape)
,cmap=plt.cm.gray
,interpolation="nearest")
plt.show()
5.3贝叶斯分类器
5.3.1 贝叶斯定理
假设 X , Y X,Y X,Y是一对随机变量,他们的联合概率 P ( X = x , Y = y ) P(X=x,Y=y) P(X=x,Y=y)是指X取值x,且Y取值y的概率,条件概率是指一随机变量在另外一随机变量取值已知的情况下取某一特定的概率。例如,条件概率 P ( Y = y ∣ X = x ) P(Y=y|X=x) P(Y=y∣X=x)是指在变量X取值x的情况下,Y变量取值y个概率。X和Y的联合概率和条件概率满足以下关系:
P ( X , Y ) = P ( Y ∣ X ) × P ( X ) = P ( X ∣ Y ) × P ( Y ) P(X,Y)=P(Y|X) \times P(X) = P(X|Y) \times P(Y) P(X,Y)=P(Y∣X)×P(X)=P(X∣Y)×P(Y)
该公式可以变换为:
P ( Y ∣ X ) = P ( X ∣ Y ) P ( Y ) P ( X ) P(Y|X)= \frac{P(X|Y)P(Y)}{P(X)} P(Y∣X)=P(X)P(X∣Y)P(Y)
该公式即为贝叶斯定理。
5.3.2 贝叶斯定理在分类中的应用
后验概率: P ( Y ∣ X ) P(Y|X) P(Y∣X)称为Y的后验概率
先验概率: P ( Y ) P(Y) P(Y)称为Y的先验概率
其中后验概率 P ( Y ∣ X ) P(Y|X) P(Y∣X)即可以表示给定属性X的条件下分到Y类的概率。那么将贝叶斯定理应用到分类任务中,我们需要找到的就是使得 P ( Y ∣ X ) P(Y|X) P(Y∣X)最大的Y,即是我们所需要分的属性X的类。
- 案例 5.3.1
| Tid | 有房 | 婚姻状况 | 年收入 | 拖欠贷款 |
|---|---|---|---|---|
| 1 | 是 | 单身 | 125K | 否 |
| 2 | 否 | 已婚 | 100K | 否 |
| 3 | 否 | 单身 | 70K | 否 |
| 4 | 是 | 已婚 | 120K | 否 |
| 5 | 否 | 离异 | 95k | 是 |
| 6 | 否 | 已婚 | 60K | 否 |
| 7 | 是 | 离异 | 220k | 否 |
| 8 | 否 | 单身 | 85k | 是 |
| 9 | 否 | 已婚 | 75K | 否 |
| 10 | 否 | 单身 | 90k | 是 |
问:现在有一属性X={有房=否,婚姻状况=已婚,年收入=120k}的记录,请问该属性是否会拖欠贷款。
那么我们现在需要做的就是去求 P ( Y e s ∣ X ) 和 P ( N o ∣ X ) P(Yes|X)和P(No|X) P(Yes∣X)和P(No∣X)的概率,我们的类就是选取后验概率最大的一类。
但是我们准确的去雇你属性值的每一种可能组合的后验概率是非常困难的,数量级是非常多的,此时,我们可以通过贝叶斯定理去计算,属性的后验概率。
P ( Y ∣ X ) = P ( X ∣ Y ) P ( Y ) P ( X ) P(Y|X)=\frac{P(X|Y)P(Y)}{P(X)} P(Y∣X)=P(X)P(X∣Y)P(Y)
在上式中,已知 P ( X ) P(X) P(X)通常为一个常数,在我们进行比较大小的时候可以忽略。 P ( Y ) P(Y) P(Y)可以通过训练集中属于每个类的训练记录所占的比例很容易地估计得出。所以我们接下俩的问题就是估计P(X|Y) 接下来我们通过两种方法实现对P(X|Y)的估计:朴素贝叶斯和贝叶斯信念网络
5.3.3 朴素贝叶斯分类器
朴素贝叶斯分类器的前提假设:条件独立。
即在朴素贝贝叶斯分类器中,我们假设在一个记录中,所有的属性之间时相互独立的,此时类条件概率可以表示为:
P ( X ∣ Y = y ) = ∏ i = 1 d P ( X i ∣ Y = y ) P(X|Y=y)=\prod_{i=1}^{d}P(X_i|Y=y) P(X∣Y=y)=i=1∏dP(Xi∣Y=y)
1.朴素贝叶斯的工作原理
有了条件独立假设,就不必计算X的每一组合的类条件概率,只需要对给定的Y,计算每一个 X i X_i Xi的条件概率。这样不需要恨到的训练集就能获得较好的概率估计。
朴素贝叶斯对Y的计算后验概率:
P ( Y ∣ X ) = P ( Y ) ∏ i = 1 d P ( X i ∣ Y ) p ( X ) P(Y|X)=\frac{P(Y)\prod_{i=1}^dP(X_i|Y)}{p(X)} P(Y∣X)=p(X)P(Y)∏i=1dP(Xi∣Y)
对于所
有的Y,P(X)是固定的,因此只需要找出使分子 P ( Y ) ∏ i = 1 d P ( X i ∣ Y ) P(Y)\prod_{i=1}^{d}P(X_i|Y) P(Y)∏i=1dP(Xi∣Y)最大的类就足够了。
2.估计连续属性的条件概率
朴素贝叶斯分类使用两种方法估计连续属性的类条件概率
(1)将连续数据离散化,将连续数据转换为序数据
(2)可以假设连续变量服从某种概率分布,然后使用训练数据估计分布的参数。高斯分布是常被用来表示连续属性的类条件概率分布,该分布有两个参数,均值 μ \mu μ和方差%\sigma^2 . 对 每 个 类 .对每个类 .对每个类y_j , 属 性 ,属性 ,属性X_i$的条件概率等于:
P ( X i = x i ∣ Y = y j ) = 1 2 π σ i j e ( x i − μ o ) 2 2 σ i j 2 P(X_i=x_i|Y=y_j)=\frac{1}{\sqrt{2\pi \sigma_{ij}}}e^{\frac{(x_i - \mu_o)^2}{2\sigma_{ij}^2}} P(Xi=xi∣Y=yj)=2πσij1e2σij2(xi−μo)2
参数 μ i j \mu_{ij} μij,可以用所有训练记录关于 X i X_i Xi的样本均值 ( ( ˉ x ) ) (\bar(x)) ((ˉx))来估计,同理,参数 σ i j 2 \sigma_{ij}^2 σij2可以用这些训练记录的样本方差 s 2 s^2 s2来估计。
- 关于上述案例:
关于上述属性关于NO的样本均值和方差:
x ˉ = 125 + 100 + 70 + . . . + 75 7 s 2 = ( 125 − 110 ) 2 + ( 100 − 110 ) 2 + . . . + ( 75 − 110 ) 2 7 = 2975 s = 2975 = 54.54 \bar{x}=\frac{125+100+70+...+75 }{7}\\ {}\\ s^2=\frac{(125-110)^2+(100-110)^2+...+(75-110)^2}{7}=2975\\ {}\\ s=\sqrt{2975}=54.54 xˉ=7125+100+70+...+75s2=7(125−110)2+(100−110)2+...+(75−110)2=2975s=2975=54.54
对于上述案例,应征税的收入等于120k美元,其类条件概率为:
P ( 收 入 = $ 120 k ∣ N o ) = 1 2 π ( 54.54 ) e − 120 − 110 2 × 2975 = 0.0072 P(收入=\$120k|No)=\frac{1}{\sqrt{2\pi}(54.54)}e^{-\frac{120-110}{2 \times 2975}}=0.0072 P(收入=$120k∣No)=2π(54.54)1e−2×2975120−110=0.0072
但是上述条件概率的解释存在一定的误导性。上述公式为一个连续的概率密度函数,当一个连续属性中取一个点的概率应该为0,在连续属性中,概率我们取一个点的小区间.
P ( x i ⩽ X i ⩽ x i + ϵ ∣ Y = y j ) = ∫ x i x i + ϵ f ( X i ; μ i j , σ i j ) d X i ≈ f ( X i ; μ i j , σ i j ) × ϵ P(x_i \leqslant X_i \leqslant x_i +\epsilon|Y=y_j)=\int_{x_i}^{x_i + \epsilon}f(X_i;\mu_{ij},\sigma_{ij})dX_i \approx f(X_i;\mu_{ij},\sigma_{ij}) \times \epsilon P(xi⩽Xi⩽xi+ϵ∣Y=yj)=∫xixi+ϵf(Xi;μij,σij)dXi≈f(Xi;μij,σij)×ϵ
由于 ϵ \epsilon ϵ是每个类的一个常量乘法因子,在对后验概率P(Y|X)进行规范化的时候就抵消掉了。因此,还可以这样来表示。
3.朴素贝叶斯分类器举例
- 案例
| Tid | 有房 | 婚姻状况 | 年收入 | 拖欠贷款 |
|---|---|---|---|---|
| 1 | 是 | 单身 | 125K | 否 |
| 2 | 否 | 已婚 | 100K | 否 |
| 3 | 否 | 单身 | 70K | 否 |
| 4 | 是 | 已婚 | 120K | 否 |
| 5 | 否 | 离异 | 95k | 是 |
| 6 | 否 | 已婚 | 60K | 否 |
| 7 | 是 | 离异 | 220k | 否 |
| 8 | 否 | 单身 | 85k | 是 |
| 9 | 否 | 已婚 | 75K | 否 |
| 10 | 否 | 单身 | 90k | 是 |
| 条件概率 |
|---|
| P ( 有 房 = 是 ∥ N o ) = 3 7 P(有房=是\|No)=3 \over 7 7P(有房=是∥No)=3 |
| P ( 有 房 = 否 ∥ N o ) = 4 7 P(有房=否\|No)=4 \over 7 7P(有房=否∥No)=4 |
| P ( 有 房 = 是 ∥ Y e s ) = 0 P(有房=是\|Yes)=0 P(有房=是∥Yes)=0 |
| P ( 有 房 = 否 ∥ Y e s ) = 1 P(有房=否\|Yes)=1 P(有房=否∥Yes)=1 |
| P ( 婚 姻 情 况 = 单 身 ∥ N o ) = 2 7 P(婚姻情况=单身\|No)=2 \over 7 7P(婚姻情况=单身∥No)=2 |
| P ( 婚 姻 情 况 = 离 婚 ∥ N o ) = 1 7 P(婚姻情况=离婚\|No)=1 \over 7 7P(婚姻情况=离婚∥No)=1 |
| P ( 婚 姻 情 况 = 已 婚 ∥ N o ) = 4 7 P(婚姻情况=已婚\|No)=4 \over 7 7P(婚姻情况=已婚∥No)=4 |
| P ( 婚 姻 情 况 = 单 身 ∥ Y e s ) = 2 3 P(婚姻情况=单身\|Yes)=2 \over 3 3P(婚姻情况=单身∥Yes)=2 |
| P ( 婚 姻 情 况 = 离 婚 ∥ Y e s ) = 1 3 P(婚姻情况=离婚\|Yes)=1 \over 3 3P(婚姻情况=离婚∥Yes)=1 |
| P ( 婚 姻 情 况 = 已 婚 ∥ Y e s ) = 0 P(婚姻情况=已婚\|Yes)=0 P(婚姻情况=已婚∥Yes)=0 |
| 年收入 |
| 如果类=No:样本均值 = 110 样本方差=2957 |
| 如果类=Yes:样本均值=90 样本均值=25 |
现在预测记录X=(有房=否,婚姻状况=已婚,年收入=$120K)的类标号,现在我们只需要计算后验概率P(No|X)和P(Yes|X).
由贝叶斯定理可得:
P ( N o ∣ X ) = P ( N o ) ∏ i = 1 d P ( X i ∣ Y ) P ( X ) = P ( N o ) P ( 有 房 = 否 ∣ N o ) P ( 婚 姻 状 况 = 已 婚 ∣ N o ) P ( 年 收 入 = 120 K ∣ N o ) P ( X ) = 0.7 × 4 7 × 4 7 × 0.0072 P ( X ) = 0.0016 α P ( Y e s ∣ X ) = P ( Y e s ) ∏ i = 1 d P ( X i ∣ Y ) P ( X ) = P ( Y e s ) P ( 有 房 = 否 ∣ Y e s ) P ( 婚 姻 状 况 = 已 婚 ∣ Y e s ) P ( 年 收 入 = 120 K ∣ Y e s ) P ( X ) = 0.3 × 1 × 0 × ( 1.2 × 1 0 − 9 ) P ( X ) = 0 \begin{aligned} P(No|X) &= \frac{P(No) \prod_{i=1}^d P(X_i|Y)}{P(X)} \\ &= \frac{ P(No) P(有房=否|No) P(婚姻状况=已婚|No) P(年收入=120K|No)}{P(X)} \\ &= \frac{0.7 \times {4\over7} \times {4\over7} \times 0.0072}{P(X)}=0.0016\alpha \\{} P(Yes|X) &= \frac{P(Yes) \prod_{i=1}^d P(X_i|Y)}{P(X)} \\ &= \frac{ P(Yes) P(有房=否|Yes) P(婚姻状况=已婚|Yes) P(年收入=120K|Yes)}{P(X)} \\ &= \frac{0.3 \times 1 \times 0 \times (1.2 \times 10^{-9})}{P(X)}=0 \end{aligned} P(No∣X)P(Yes∣X)=P(X)P(No)∏i=1dP(Xi∣Y)=P(X)P(No)P(有房=否∣No)P(婚姻状况=已婚∣No)P(年收入=120K∣No)=P(X)0.7×74×74×0.0072=0.0016α=P(X)P(Yes)∏i=1dP(Xi∣Y)=P(X)P(Yes)P(有房=否∣Yes)P(婚姻状况=已婚∣Yes)P(年收入=120K∣Yes)=P(X)0.3×1×0×(1.2×10−9)=0
假设 α = 1 P ( X ) \alpha = 1 \over P(X) P(X)α=1是一个常量,通过比较可以得出记录的分类为No。
4.条件概率的m估计
前面的例子体现了从训练数据估计后验概率时的一个潜在问题:如果有一个数学的类条件概率等于0,则整个类的后验概率就等于0.仅使用记录比例来估计类体哦阿健概率的方法显的太脆弱。
解决该问题的途径是使用m估计:
P ( x i ∣ y j ) = n c + m p n + m P(x_i|y_j)=\frac{n_c+mp}{n+m} P(xi∣yj)=n+mnc+mp
其中n是类 y j y_j yj中的实例总数。 n c n_c nc是类 y j y_j yj的训练样例中取值 x i x_i xi的样例数,m是称为等价样本大小的参数,p是用户指定的参数。如果没有训练集(即n=0),则 P ( x i ∣ y j ) = p P(x_i|y_j)=p P(xi∣yj)=p.因此p可以看作是在类 y j y_j yj的记录中观察属性值 x i x_i xi的先验概率。等价样本大小决定先验概率p和观测概率 n c / n n_c/n nc/n之间的平衡。
在前面的例子中,条件概率P(婚姻状况=已婚|Yes)=0,因为类中没有训练样例含有该属性值。使用m的估计方法, m=3(婚姻状况分为3类),n=3(例子中Yes类有3条记录), P=1/3,则条件概率不再是0:
P ( 婚 姻 状 况 = 已 婚 ∣ Y e s ) = ( 0 + 3 × 1 / 3 ) / ( 3 + 3 ) = 1 / 6 P ( N o ∣ X ) = P ( N o ) ∏ i = 1 d P ( X i ∣ Y ) P ( X ) = P ( N o ) P ( 有 房 = 否 ∣ N o ) P ( 婚 姻 状 况 = 已 婚 ∣ N o ) P ( 年 收 入 = 120 K ∣ N o ) P ( X ) = 0.7 × 6 10 × 6 10 × 0.0072 P ( X ) = 0.0018 α P ( Y e s ∣ X ) = P ( Y e s ) ∏ i = 1 d P ( X i ∣ Y ) P ( X ) = P ( Y e s ) P ( 有 房 = 否 ∣ Y e s ) P ( 婚 姻 状 况 = 已 婚 ∣ Y e s ) P ( 年 收 入 = 120 K ∣ Y e s ) P ( X ) = 0.3 × 4 6 × 1 6 × ( 1.2 × 1 0 − 9 ) P ( X ) = 4.0 × 1 0 − 11 α \begin{aligned} P(婚姻状况&=已婚|Yes)=(0 + 3 \times 1/3)/(3+3)=1/6\\ P(No|X) &= \frac{P(No) \prod_{i=1}^d P(X_i|Y)}{P(X)} \\ &= \frac{ P(No) P(有房=否|No) P(婚姻状况=已婚|No) P(年收入=120K|No)}{P(X)} \\ &= \frac{0.7 \times {6\over10} \times {6\over10} \times 0.0072}{P(X)}=0.0018\alpha \\{} P(Yes|X) &= \frac{P(Yes) \prod_{i=1}^d P(X_i|Y)}{P(X)} \\ &= \frac{ P(Yes) P(有房=否|Yes) P(婚姻状况=已婚|Yes) P(年收入=120K|Yes)}{P(X)} \\ &= \frac{0.3 \times {4 \over 6} \times {1 \over 6} \times (1.2 \times 10^{-9})}{P(X)}=4.0\times 10^{-11} \alpha \end{aligned} P(婚姻状况P(No∣X)P(Yes∣X)=已婚∣Yes)=(0+3×1/3)/(3+3)=1/6=P(X)P(No)∏i=1dP(Xi∣Y)=P(X)P(No)P(有房=否∣No)P(婚姻状况=已婚∣No)P(年收入=120K∣No)=P(X)0.7×106×106×0.0072=0.0018α=P(X)P(Yes)∏i=1dP(Xi∣Y)=P(X)P(Yes)P(有房=否∣Yes)P(婚姻状况=已婚∣Yes)P(年收入=120K∣Yes)=P(X)0.3×64×61×(1.2×10−9)=4.0×10−11α
尽管分类结果不变,但是当训练样例较少时,m估计通常时一种更加健壮的概率估计方法。
5.3.4 贝叶斯误差率
假定任务是通过体长来区分美洲鳄和普通鳄鱼。决策边界为 x ^ \hat{x} x^,则此任务的误差率为:
E r r o r = ∫ 0 x ^ P ( 鳄 鱼 ∣ X ) d X + ∫ x ^ ∞ P ( 美 洲 鳄 ∣ X ) d X Error = \int_0^{\hat{x}}P(鳄鱼|X)dX + \int_{\hat{x}}^{\infin}P(美洲鳄|X)dX Error=∫0x^P(鳄鱼∣X)dX+∫x^∞P(美洲鳄∣X)dX
该误差称为贝叶斯误差率。
5.3.5贝叶斯信念网络
朴素贝叶斯分类器的前提条件是各个属性之间都是相互独立的,但是这样的假设过于严格。贝叶斯网络是一种灵活的建模方法,该方法不要求给定类的所有属性都条件独立,而是允许指定哪些属性条件独立。
1.模型表示
贝叶斯信念网络(Bayesian belief network,BBN)简称贝叶斯网络,用图形表示一组随机变量之间的概率关系。贝叶斯网络有两个主要成分:
2.建立模型
| 算法5.3 贝叶斯网络括扑结构的生成算法 |
|---|
| 1:设 T = ( X 1 , X 2 , . . . , X d ) T=(X_1,X_2,...,X_d) T=(X1,X2,...,Xd)表示变量的全序 |
| 2:for j=1 to d do |
| 3: 令 X T ( j ) X_{T(j)} XT(j)表示T中第j个次序最高的变量 |
| 4: 令 π ( X T ( j ) ) = { X T ( 1 ) , X T ( 2 ) . . . X T ( j − 1 ) } \pi(X_{T(j)})=\{X_{T(1)},X_{T(2)}...X_{T(j-1)}\} π(XT(j))={XT(1),XT(2)...XT(j−1)}表示排在 X T ( j ) X_{T(j)} XT(j)前面的变量的集合 |
| 5:从 π ( X T ( j ) ) \pi(X_{T(j)}) π(XT(j))中去掉对 X j X_{j} Xj没有影响的变量(使用先验知识) |
| 6:在 X T ( j ) X_{T(j)} XT(j)和 π ( X T ( j ) ) \pi(X_{T(j)}) π(XT(j))中剩余的变量之间画弧 |
| 7:end for |
3.举例
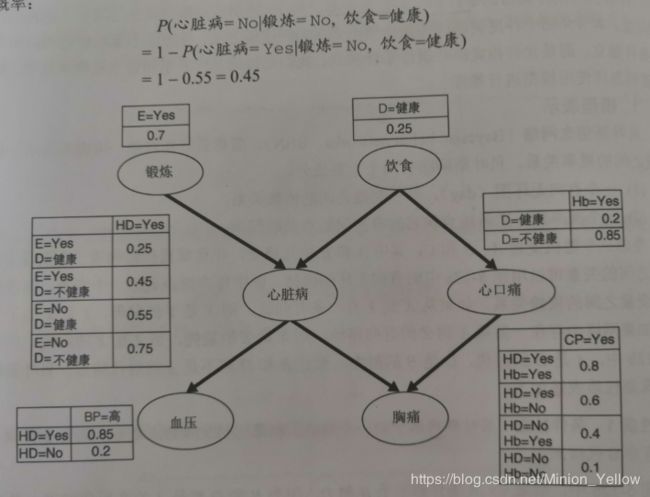
对于上图中的案例,通过举例来对BBN进行推理。
情况一:没有先验信息在没有任何先验信息的情况下,可以通过计算先验概率P(HD=Yes)和P(HD=No)来确定一个人是否可能患心脏病。为了表述方便,设 α ∈ { Y e s , N o } \alpha \in \{Yes,No\} α∈{Yes,No}表示锻炼的两个值 β ∈ { 健 康 , 不 健 康 } \beta \in \{健康,不健康\} β∈{健康,不健康}表示饮食的两个值。
P ( H D = Y e s ) = ∑ α ∑ β P ( H D = Y e s ∣ E = α , D = β ) P ( E = α , D = β ) = ∑ α ∑ β P ( H D = Y e s ∣ E = α , D = β ) P ( E = α ) P ( D = β ) = 0.25 × 0.7 × 0.25 + 0.45 × 0.7 × 0.75 + 0.55 × 0.3 × 0.25 + 0.75 × 0.3 × 0.75 = 0.49 \begin{aligned} P(HD=Yes) &= \sum_\alpha \sum_\beta P(HD=Yes|E=\alpha,D=\beta)P(E=\alpha,D=\beta)\\ &= \sum_\alpha \sum_\beta P(HD=Yes|E=\alpha,D=\beta)P(E=\alpha)P(D=\beta)\\ &= 0.25 \times 0.7 \times 0.25 + 0.45 \times 0.7 \times 0.75 + 0.55 \times 0.3 \times0.25 +0.75\times0.3\times0.75\\ &=0.49 \end{aligned} P(HD=Yes)=α∑β∑P(HD=Yes∣E=α,D=β)P(E=α,D=β)=α∑β∑P(HD=Yes∣E=α,D=β)P(E=α)P(D=β)=0.25×0.7×0.25+0.45×0.7×0.75+0.55×0.3×0.25+0.75×0.3×0.75=0.49
因为P(HD=No)=1-P(HD=Yes)=0.511,所以此人不得心脏病的记录略微大一点。
情况二:高血压 如果一个人有高血压,可以通过比较后验概率P(HD=Yes|BP=高)和P(HD=No|BP=高)来诊断他是否患有心脏病。为此,我们必须先计算P(BP=高):
P ( B P = 高 ) = ∑ γ p ( B P = 高 ∣ H D = γ ) P ( H D = γ ) = 0.85 × 0.49 + 0.2 × 0.51 = 0.5185 其 中 γ ∈ y e s , N o 。 因 此 , 此 人 患 有 心 脏 病 的 后 验 概 率 是 : P ( H D = Y e s ∣ B P = 高 ) = P ( B P = 高 ∣ H D = Y e s ) P ( H D = Y e s ) P ( B P = 高 ) = 0.85 × 0.49 0.5185 = 0.8033 同 理 , P ( H D = N o ∣ B p = 高 ) = 1 − 0.8033 = 0.1967 \begin{aligned} P(BP=高)&=\sum_{\gamma}p(BP=高|HD=\gamma)P(HD=\gamma)\\ &=0.85\times 0.49 + 0.2 \times 0.51 = 0.5185 \end{aligned} {}\\ 其中\gamma \in {yes,No}。因此,此人患有心脏病的后验概率是:\\ {}\\ \begin{aligned} P(HD=Yes|BP=高)&=\frac{P(BP=高|HD=Yes)P(HD=Yes)}{P(BP=高)} \\ &=\frac{0.85 \times 0.49}{0.5185} = 0.8033 \end{aligned}\\ {}\\ 同理,P(HD=No|Bp=高)=1-0.8033=0.1967 P(BP=高)=γ∑p(BP=高∣HD=γ)P(HD=γ)=0.85×0.49+0.2×0.51=0.5185其中γ∈yes,No。因此,此人患有心脏病的后验概率是:P(HD=Yes∣BP=高)=P(BP=高)P(BP=高∣HD=Yes)P(HD=Yes)=0.51850.85×0.49=0.8033同理,P(HD=No∣Bp=高)=1−0.8033=0.1967
所以当一个人患有高血压时,他患有心脏病的危险就增加了。
情况三:高血压,饮食健康,经常锻炼身体假设得知此人经常锻炼身体,并且饮食健康。这些新信息会对诊断造成新的影响。则此人患有心脏病的后验概率为:
P ( H D = Y e s ∣ B P = 高 , D = 健 康 , E = Y e s ) = [ P ( B P = 高 ∣ H D = Y e s , D = 健 康 , E = Y e s ) P ( B P = 高 ∣ D = 健 康 , E = Y e s ) ] × P ( H D = Y e s ∣ D = 健 康 , E = Y e s ) = P ( B P = 高 ∣ H D = Y e s ) P ( H D = Y e s ∣ D = 健 康 , E = Y e s ) ∑ g a m m a P ( B P = 高 ∣ H D = γ ) P ( H D = γ ∣ D = 健 康 , E = Y e s ) = 0.85 × 0.25 0.85 × 0.25 + 0.2 × 0.75 = 0.5862 则 此 人 不 换 心 脏 病 的 概 率 是 : P ( H D = N o ∣ B P = 高 , D = 健 康 , E = Y e s ) = 1 − 0.5862 = 0.4138 \begin{aligned} &P(HD=Yes|BP=高,D=健康,E=Yes)\\ &=[\frac{P(BP=高|HD=Yes,D=健康,E=Yes)}{P(BP=高|D=健康,E=Yes)}]\times P(HD=Yes|D=健康,E=Yes)\\ &=\frac{P(BP=高|HD=Yes)P(HD=Yes|D=健康,E=Yes)}{\sum_{gamma}P(BP=高|HD=\gamma)P(HD=\gamma|D=健康,E=Yes)}\\ &=\frac{0.85\times0.25}{0.85\times0.25+0.2\times0.75}\\ &=0.5862 \end{aligned}\\ 则此人不换心脏病的概率是:\\ P(HD=No|BP=高,D=健康,E=Yes)=1-0.5862=0.4138 P(HD=Yes∣BP=高,D=健康,E=Yes)=[P(BP=高∣D=健康,E=Yes)P(BP=高∣HD=Yes,D=健康,E=Yes)]×P(HD=Yes∣D=健康,E=Yes)=∑gammaP(BP=高∣HD=γ)P(HD=γ∣D=健康,E=Yes)P(BP=高∣HD=Yes)P(HD=Yes∣D=健康,E=Yes)=0.85×0.25+0.2×0.750.85×0.25=0.5862则此人不换心脏病的概率是:P(HD=No∣BP=高,D=健康,E=Yes)=1−0.5862=0.4138
通过此结果可以看出健康的饮食和有规律的锻炼可以降低患心脏病的危险。
5.3.6 贝叶斯模型代码实现
sklearn中,朴素贝叶斯根据预测 P ( x i ∣ y ) P(x_i|y) P(xi∣y)分布时,所作假设不同,有:
- 高斯朴素贝叶斯:GaussianNB()
- 多项式朴素贝叶斯:multinomialNB()
- 伯努利朴素贝叶斯:BernoulliNB()
- 补充朴素贝叶斯: ComplementNB()
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
iris=datasets.load_iris()
Xtrain,Xtest,Ytrain,Ytest = train_test_split(iris.data,iris.target,test_size=0.3)
gnb = GaussianNB()
gnb.fit(Xtrain,Ytrain)
scores = gnb.score(Xtest,Ytest)
print(scores)
y_pred = gnb.predict(iris.data)
print("Number of mislabeled points out of a total %d points : %d"% (iris.data.shape[0],(iris.target != y_pred).sum()))
输出:
0.9111111111111111
Number of mislabeled points out of a total 150 points : 6
5.4人工神经网络
(略)参见专门人工神经网络分类
5.5支持向量机(SVM)
支持向量机模型根据数据的分布可以分为线性可分、线性不可分、非线性支持向量机。
5.5.1 最大边缘超平面
在上图的数据中有实心点和空心点两类,我们可以在两类数据中间找到无数条线,使两类数据分开,但是边缘(虚线之间的距离)越大,说明我们的分类器的抗泛化能力就越强,所以当构建模型时,我们应寻找最大边缘超平面。这个思想将通篇贯穿在支持向量机当中。
5.5.2 线性支持向量机:可分情况
1.线性决策边界
考 虑 一 个 包 含 N 个 训 练 样 本 的 二 元 分 类 问 题 , 每 个 样 本 表 示 为 一 个 二 元 组 ( x i , y i ) , ( i = 1 , 2... N ) 其 中 x i = ( x i 1 , x i 2 . . . x i 3 ) T , 对 应 于 第 i 个 样 本 的 属 性 集 , y i ∈ { 1 , − 1 } 表 示 它 的 类 标 号 。 择 一 个 线 性 分 类 器 的 决 策 边 界 可 以 写 成 如 下 形 式 : W ⋅ X + b = 0 其 中 W 和 b 是 模 型 的 参 数 。 考虑一个包含N个训练样本的二元分类问题,\\ 每个样本表示为一个二元组(x_i,y_i),(i=1,2...N)\\ 其中x_i=(x_{i1},x_{i2}...x_{i3})^T,对应于第i个样本的属性集,\\ y_i \in \{1,-1\}表示它的类标号。\\ 择一个线性分类器的决策边界可以写成如下形式:\\ {}\\ W \cdot X + b =0\\ 其中W和b是模型的参数。 考虑一个包含N个训练样本的二元分类问题,每个样本表示为一个二元组(xi,yi),(i=1,2...N)其中xi=(xi1,xi2...xi3)T,对应于第i个样本的属性集,yi∈{1,−1}表示它的类标号。择一个线性分类器的决策边界可以写成如下形式:W⋅X+b=0其中W和b是模型的参数。
对于决策边界上方的点 x s x_s xs可以证明:
w ⋅ x s + b > 0 w \cdot x_s +b > 0 w⋅xs+b>0
对于决策边界下方的点 x c x_c xc可以证明:
w ⋅ x c + b < 0 w \cdot x_c +b < 0 w⋅xc+b<0
所以可以用以下式子来预测样本z的类标号y:
y = { 1 , 如 果 w ⋅ z + b > 0 − 1 , 如 果 w ⋅ z + b < 0 y=\begin{cases} 1,如果w \cdot z +b>0\\ -1,如果w \cdot z +b<0 \\ \end{cases} y={1,如果w⋅z+b>0−1,如果w⋅z+b<0
2.线性分类器的边缘
考虑哪些离决策边缘最近的点,调整参数w和b,两条平行于决策边界的超平面为:
l 1 : w ⋅ x + b = 1 l 2 : w ⋅ x + b = − 1 l_1:w \cdot x +b =1\\ l_2:w \cdot x + b =-1\\ l1:w⋅x+b=1l2:w⋅x+b=−1
假设 x 1 x_1 x1是 l 1 l_1 l1上的一点, x 2 x_2 x2是 l 2 l_2 l2上的一点,则可以计算两个超平面之间的距离:
两 个 超 平 面 相 减 得 : w ⋅ ( x 1 − x 2 ) = 2 ∣ ∣ w ∣ ∣ ⋅ d = 2 d = 2 ∣ ∣ w ∣ ∣ 两个超平面相减得:\\ {}\\ w\cdot (x_1 -x_2) =2\\ ||w|| \cdot d = 2 \\ d = \frac{2}{||w||} 两个超平面相减得:w⋅(x1−x2)=2∣∣w∣∣⋅d=2d=∣∣w∣∣2
3.学习线性SVM模型
SVM的训练阶段包括从训练中估计决策边界的参数w和b,参数w和b必须满足下面的两个条件:
w ⋅ x i + b ≥ 1 , 如 果 y i = 1 w ⋅ x i + b ≤ 1 , 如 果 y i = − 1 这 两 个 式 子 可 以 概 括 为 如 下 的 形 式 : y i ( w ⋅ x i + b ) ≥ 1 , i = 1 , 2... , N 此 外 , S V M 学 习 到 的 参 数 w 和 b 除 了 满 足 上 面 的 式 子 外 , 还 应 该 使 决 策 边 缘 d = 2 ∣ ∣ w ∣ ∣ 最 大 , d 最 大 等 价 于 下 面 的 目 标 函 数 最 小 : f ( w ) = ∣ ∣ w ∣ ∣ 2 2 w \cdot x_i +b \geq 1 ,如果y_i=1\\ w \cdot x_i +b \leq 1,如果y_i=-1\\ 这两个式子可以概括为如下的形式:\\ y_i(w \cdot x_i + b) \geq 1,i=1,2...,N\\ 此外,SVM学习到的参数w和b除了满足上面的式子外,\\ 还应该使决策边缘d=\frac{2}{||w||}最大,d最大等价于下面的目标函数最小:\\ f(w)=\frac{||w||^2}{2}\\ w⋅xi+b≥1,如果yi=1w⋅xi+b≤1,如果yi=−1这两个式子可以概括为如下的形式:yi(w⋅xi+b)≥1,i=1,2...,N此外,SVM学习到的参数w和b除了满足上面的式子外,还应该使决策边缘d=∣∣w∣∣2最大,d最大等价于下面的目标函数最小:f(w)=2∣∣w∣∣2
所以通过上面的分析,SVM模型的线性可分模型可以总结为下述问题:
SVM线性可分的优化问题:
min w ∣ ∣ w ∣ ∣ 2 2 y i ( w ⋅ x y i + b ) ≥ 1 , i = 1 , 2 , . . . , N \min \limits_{w}\frac{||w||^2}{2}\\ y_i(w \cdot x_yi + b) \geq 1 , i=1,2,...,N wmin2∣∣w∣∣2yi(w⋅xyi+b)≥1,i=1,2,...,N
现在我们需要解的问题就是求上面的优化问题,优化问题中,目标函数是二次的,约束条件是关于w和b的线性的,因此这个问题是一个凸优化问题。所以可以通过标准的拉格朗日乘子法解该优化问题。
拉 格 朗 日 函 数 : L p = 1 2 ∣ ∣ w ∣ ∣ 2 − ∑ i = 1 N λ i ( y i ( w ⋅ x i + b ) − 1 ) 最 小 化 L p , 通 过 L p 对 w 和 b 求 偏 导 : ∂ L p ∂ w − − > w = ∑ i = 1 N λ i y i x i ∂ L p ∂ b − − > ∑ i = 1 N λ i y i = 0 拉格朗日函数:L_p={1 \over 2}||w||^2-\sum_{i=1}^{N}\lambda_i(y_i(w \cdot x_i + b)-1)\\ 最小化L_p,通过L_p对w和b求偏导:\\ {}\\ \frac{\partial{L_p}}{\partial{w}}-->w=\sum_{i=1}^N \lambda_i y_i x_i \\ \frac{\partial{L_p}}{\partial{b}}-->\sum_{i=1}^{N}\lambda_iy_i=0 拉格朗日函数:Lp=21∣∣w∣∣2−i=1∑Nλi(yi(w⋅xi+b)−1)最小化Lp,通过Lp对w和b求偏导:∂w∂Lp−−>w=i=1∑Nλiyixi∂b∂Lp−−>i=1∑Nλiyi=0
但是这样我们仍然得不到w和b的解,因为KaTeX parse error: Undefined control sequence: \ambda at position 1: \̲a̲m̲b̲d̲a̲是未知的,但是如果优化问题中的约束条件为等式约束,那么我们就可以通过N个等式加上偏导便可以解出w,b和 λ \lambda λ。
将不等式约束转换为等式约束需要使用到KKT条件:
λ i ≥ 0 λ i [ y i ( w i ⋅ x i + b ) − 1 ] = 0 \lambda_i \geq 0 \\ {}\\ \lambda_i[y_i(w_i \cdot x_i+b)-1]=0 λi≥0λi[yi(wi⋅xi+b)−1]=0
但是对于这样的问题求解仍然是一个复杂的问题,所以我们可以通过求它的对偶问题:
L D = ∑ i = 1 N λ i − 1 2 ∑ i , j λ i λ j y i y j x i ⋅ x j L_D=\sum_{i=1}^{N}\lambda_i - \frac{1}{2}\sum_{i,j}\lambda_i \lambda_jy_iy_jx_i \cdot x_j LD=i=1∑Nλi−21i,j∑λiλjyiyjxi⋅xj
这样原问题的最小化,变为了求对偶问题的最大化。其对偶问题只涉及到了训练数据和拉格朗日乘子。
求出拉格朗日乘子后决策边界可以表示为:
( ∑ i = 1 N λ i y i x i ⋅ x ) + b = 0 (\sum_{i=1}^{N}\lambda_iy_ix_i \cdot x)+b =0 (i=1∑Nλiyixi⋅x)+b=0
b可以求解支持向量公式 λ i [ y i ( w ⋅ x i + b ) − 1 ] = 0 \lambda_i[y_i(w \cdot x_i +b)-1]=0 λi[yi(w⋅xi+b)−1]=0,由于求解过程是数值计算得到的,所以b的值不唯一,我们在计算的过程中取b的平均数。
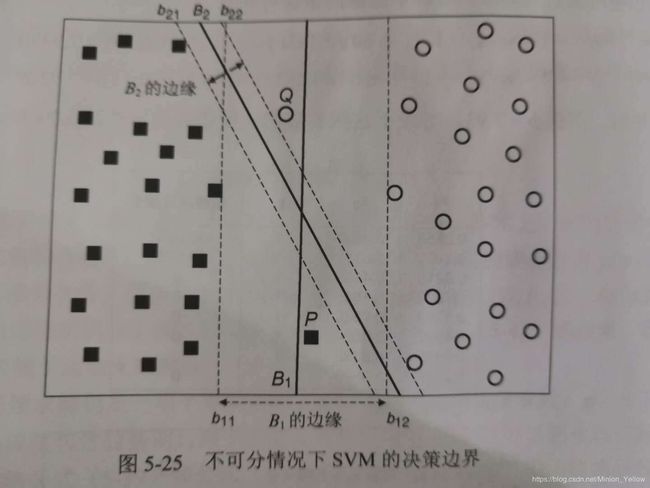
5.5.3 线性支持向量机:不可分情况
考虑如图的情况,虽然决策边界B2的划分为B1更加的精确,但是B1却是一个比B2"好"的模型,因为B1虽然包含着两个错误的案例,但是B1的边缘更宽,所以B1的泛化能力更强。这一节来修正公式完成这种操作,这种决策边界称为软边缘。
属于B1决策边界的鲁棒性更强,但是B1不再满足所有给定的约束,这时我们引入的“松弛变量”:
w ⋅ x i + b ≥ 1 − ξ i , 如 果 y i = 1 w ⋅ x i + b ≤ − 1 + ξ i , 如 果 y i = − 1 其 中 , ∀ i : ξ i > 0 。 w \cdot x_i +b \ge 1-\xi_i,如果y_i=1\\ w \cdot x_i + b \le -1 + \xi_i,如果y_i=-1\\ 其中,\forall i: \xi_i >0。 w⋅xi+b≥1−ξi,如果yi=1w⋅xi+b≤−1+ξi,如果yi=−1其中,∀i:ξi>0。
加入松弛变量后可以构建泛化能力较强决策边缘,由于最大边缘理论,我们需要使边缘最大化,但是如果使边缘最大化,松弛变量将会一直大下去,造成被错分的类增多,模型发生欠拟合。所以我们在目标函数后加一个关于松弛变量的惩罚项。因此目标函数修正为:
f ( x ) = ∣ ∣ w ∣ ∣ 2 2 + C ( ∑ i = 1 N ξ i ) 2 C 和 k 都 为 用 户 指 定 的 惩 罚 项 的 参 数 。 f(x)=\frac{||w||^2}{2}+C(\sum_{i=1}^{N}\xi_i)^2\\ C和k都为用户指定的惩罚项的参数。 f(x)=2∣∣w∣∣2+C(i=1∑Nξi)2C和k都为用户指定的惩罚项的参数。
所以通过被修正后的拉格朗日函数为:
L p = 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 N ξ i − ∑ i = 1 N λ i { y i ( w ⋅ x i + b ) − 1 + ξ i } − ∑ i = 1 N μ i ξ i L_p = \frac{1}{2}||w||^2 + C\sum_{i=1}^{N}\xi_i-\sum_{i=1}^{N}\lambda_i\{y_i(w \cdot x_i +b)-1+\xi_i\}-\sum_{i=1}^{N}\mu_i \xi_i Lp=21∣∣w∣∣2+Ci=1∑Nξi−i=1∑Nλi{yi(w⋅xi+b)−1+ξi}−i=1∑Nμiξi
使用KKT条件,将不等式约束变换为等式约束:
ξ ≥ 0 , λ i ≥ 0 , μ ≥ 0 λ i { y i ( w ⋅ x i + b ) − 1 + ξ i } = 0 μ i ξ i = 0 \xi \ge0,\lambda_i \ge 0,\mu \ge 0\\ \lambda_i\{y_i(w \cdot x_i +b)-1+ \xi_i\}=0\\ \mu_i \xi_i = 0 ξ≥0,λi≥0,μ≥0λi{yi(w⋅xi+b)−1+ξi}=0μiξi=0
令L关于w,b和 ξ i \xi_i ξi的一阶导数为零:
∂ L ∂ w j = w i − ∑ i = 1 N λ i y i x i j = 0 − − > w j = ∑ i = 1 N λ i y i x i j ∂ L ∂ b = − ∑ i = 1 N λ i y i = 0 − − > ∑ i = 1 N λ i y i = 0 ∂ L ∂ ξ i = C − λ i − μ i = 0 − − > λ i + μ i = C \begin{aligned} \frac{\partial{L}}{\partial w_j}&=w_i - \sum_{i=1}^N \lambda_i y_i x_{ij} = 0 -->w_j=\sum_{i=1}^N \lambda_i y_i x_{ij}\\ \frac{\partial{L}}{\partial b}&=-\sum_{i=1}^{N}\lambda_i y_i =0 -->\sum_{i=1}^{N}\lambda_iy_i =0\\ \frac{\partial L}{\partial \xi_i}&=C-\lambda_i-\mu_i = 0 --> \lambda_i + \mu_i =C \end{aligned} ∂wj∂L∂b∂L∂ξi∂L=wi−i=1∑Nλiyixij=0−−>wj=i=1∑Nλiyixij=−i=1∑Nλiyi=0−−>i=1∑Nλiyi=0=C−λi−μi=0−−>λi+μi=C
将上面的导数为0的条件和KKT条件代入原拉格朗日函数可得:
L D = ∑ i = 1 N λ i − 1 2 ∑ i , j λ i λ j y i y j x i ⋅ x j L_D=\sum_{i=1}^{N}\lambda_i - \frac{1}{2}\sum_{i,j}\lambda_i\lambda_jy_iy_jx_i \cdot x_j LD=i=1∑Nλi−21i,j∑λiλjyiyjxi⋅xj
然后可以使用二次规划技术,求对偶问题的数值解,得到拉格朗日乘子。从而得到决策边界。
5.5.4 非线性支持向量机
上面我们介绍的SVM模型都是线性的,这一节我们来构建非线性的SVM模型,非线性的SVM关键使在于将数据从原来的坐标空间x变换到一个新的坐标空 Φ ( x ) \Phi(x) Φ(x)中,从而可以在变换后的空间中使用一个线性的巨册边界来划分样本,进行变化后,就可以应用前面介绍的线性可分的决策边界。
1,属性变换
图(a)的分类情况:
y ( x 1 , x 2 ) = { 1 , 如 果 ( x 1 − 0.5 ) 2 + ( x 2 − 0.5 ) 2 > 0.2 − 1 , 否 则 y(x_1,x_2)= \begin{cases} 1,如果\sqrt{(x_1-0.5)^2+(x_2-0.5)^2}>0.2\\ -1,否则 \end{cases} y(x1,x2)={1,如果(x1−0.5)2+(x2−0.5)2>0.2−1,否则
图(a)的的决策边界表示为:
( x 1 − 0.5 ) 2 + ( x 2 − 0.5 ) 2 = 0.2 进 一 步 简 化 为 : x 1 2 − x 1 + x 2 2 − x 2 = − 0.46 通 过 下 面 的 变 换 Φ ( x ) 可 以 将 数 据 映 射 到 一 个 新 的 空 间 : Φ : ( x 1 , x 2 ) − − > ( x 1 2 , x 2 2 , 2 x 1 , 2 x 2 , 2 x 1 x 2 , 1 ) 在 变 换 后 的 空 间 中 寻 找 参 数 w = ( w 0 , w 1 , . . . , w 5 ) 使 得 : w 5 x 1 2 + w 4 x 2 2 + w 3 2 x 1 + w 2 2 x 2 + w 1 2 x 1 x 2 + w 0 = 0 \sqrt{(x_1-0.5)^2+(x_2-0.5)^2}=0.2\\ {}\\ 进一步简化为:\\ {}\\ x_1^2 - x_1 + x_2^2-x_2=-0.46\\ {}\\ 通过下面的变换\Phi(x)可以将数据映射到一个新的空间:\\ {}\\ {}\\ \Phi:(x_1,x_2)-->(x_1^2,x_2^2,\sqrt{2}x_1,\sqrt{2}x_2,\sqrt{2}x_1x_2,1)\\ {}\\ 在变换后的空间中寻找参数w=(w_0,w_1,...,w_5)使得:\\ {}\\ w_5x_1^2+w_4x_2^2+w_3\sqrt{2}x_1+w_2\sqrt{2}x_2+w_1\sqrt{2}x_1x_2 + w_0 =0 (x1−0.5)2+(x2−0.5)2=0.2进一步简化为:x12−x1+x22−x2=−0.46通过下面的变换Φ(x)可以将数据映射到一个新的空间:Φ:(x1,x2)−−>(x12,x22,2x1,2x2,2x1x2,1)在变换后的空间中寻找参数w=(w0,w1,...,w5)使得:w5x12+w4x22+w32x1+w22x2+w12x1x2+w0=0
以 x 1 2 − x 1 x_1^2-x_1 x12−x1和 x 2 2 − x 2 x_2^2-x_2 x22−x2为坐标绘图得到图(b)。
2.学习非线性SVM模型
通过属性变换看似是一个可行的方法,但是依然存在着一些问题:
-
- 不清楚应当使用什么类型的映射函数
-
- 在维空间中解约束优化问题仍然是一个困难的事情
我们假定存在着一个合适的映射 Φ ( x ) \Phi(x) Φ(x),在变换后的空间中,线性决策边界为 w ⋅ Φ ( x ) + b = 0 w \cdot \Phi(x) +b =0 w⋅Φ(x)+b=0
定义 非线性SVM非线性SVM的学习任务可以形式化地表达为以下的问题:
min w ∣ ∣ w ∣ ∣ 2 2 y i ( w ⋅ Φ ( x i ) + b ) ≥ 1 , i = 1 , 2 , . . . , N \min\limits_{w} \frac{||w||^2}{2}\\ {}\\ y_i(w \cdot \Phi(x_i)+b) \ge 1 ,i=1,2,...,N wmin2∣∣w∣∣2yi(w⋅Φ(xi)+b)≥1,i=1,2,...,N
通过线性SVM使用的方法,可以得到该约束问题的优化问题的对偶的拉格朗日函数:
L D = ∑ i = 1 n λ i − 1 2 ∑ i , j λ i λ j y i y j Φ ( x i ) ⋅ Φ ( x ) ( x j ) L_D = \sum_{i=1}^n \lambda_i - \frac{1}{2} \sum_{i,j}\lambda_i\lambda_jy_iy_j\Phi(x_i)\cdot\Phi(x)(x_j) LD=i=1∑nλi−21i,j∑λiλjyiyjΦ(xi)⋅Φ(x)(xj)
使用二次规划技术得到\lambda_i 后,可以通过下面的方差导出参数w和b:
w = ∑ i λ i y i Φ ( x i ) λ i { y i ∑ j λ j y j ( Φ ( x j ) ⋅ Φ ( x i ) + b ) − 1 } = 0 w=\sum_i \lambda_i y_i \Phi(x_i)\\ \lambda_i\{y_i\sum_j\lambda_jy_j(\Phi(x_j)\cdot\Phi(x_i)+b)-1\}=0 w=i∑λiyiΦ(xi)λi{yij∑λjyj(Φ(xj)⋅Φ(xi)+b)−1}=0
最后,可以通过下式对检验实例z进行分类:
f ( z ) = s i g n ( w ⋅ Φ ( z ) + b ) = s i g n ( ∑ i = 1 n λ j y j Φ ( x i ) ⋅ Φ ( z ) + b ) f(z)=sign(w \cdot \Phi(z) +b)=sign(\sum_{i=1}^{n}\lambda_jy_j\Phi(x_i)\cdot\Phi(z)+b) f(z)=sign(w⋅Φ(z)+b)=sign(i=1∑nλjyjΦ(xi)⋅Φ(z)+b)
3.核技术
通过上面的符号函数发现,点积 Φ ( x i ) ⋅ Φ ( x j ) \Phi(x_i) \cdot \Phi(x_j) Φ(xi)⋅Φ(xj),可以看作两个实例 x i , x j x_i,x_j xi,xj在变换后的空间中的相似度量。核技术是一种使用原属性集计算变换后的空间中相似度的方法。也就是说上面变换后的点积计算可以转换为运算前的相似性度量。
例如上式中的映射点积计算:
Φ ( u ) ⋅ Φ ( v ) = ( u 1 2 , u 2 2 , 2 u 1 , 2 u 2 , 2 u 1 u 2 , 1 ) ⋅ ( v 1 2 , v 2 2 , 2 v 1 , 2 v 2 , 2 v 1 v 2 , 1 ) = ( u ⋅ v + 1 ) 2 \Phi(u) \cdot \Phi(v) \\ {}\\ =(u_1^2,u_2^2,\sqrt{2}u_1,\sqrt{2}u_2,\sqrt{2}u_1u_2,1) \cdot (v_1^2,v_2^2,\sqrt{2}v_1,\sqrt{2}v_2,\sqrt{2}v_1v_2,1)\\ {}\\ =(u \cdot v+1)^2 Φ(u)⋅Φ(v)=(u12,u22,2u1,2u2,2u1u2,1)⋅(v12,v22,2v1,2v2,2v1v2,1)=(u⋅v+1)2
通过上面的计算,变换后的空间中的点积可以用原空间中的相似度函数表示:
K ( u , v ) = Φ ( u ) ⋅ ϕ ( v ) = ( u ⋅ v + 1 ) 2 K(u,v)=\Phi(u)\cdot \phi(v)=(u\cdot v+1)^2 K(u,v)=Φ(u)⋅ϕ(v)=(u⋅v+1)2
这个在原属性空间中计。算的相似度函数K称为核函数,非线性SVM中使用的核函数必须满足一个Mercer定理的数学原理,因此我们不需要知道映射函数 Φ \Phi Φ的具体形式,只需要使核函数满足Mercer定理,Mercer定理确保了核函数总可以用某高维空间中两个输入向量的点积表示。
经过核函数变化,上一节中的分类函数可以表示为:
f ( z ) = s i g n ( ∑ i = 1 n λ j y j Φ ( x i ) ⋅ Φ ( z ) + b ) s i g n ( ∑ i − 1 n λ i y i ( x i ⋅ z + 1 ) 2 + b ) f(z)=sign(\sum_{i=1}^{n}\lambda_jy_j\Phi(x_i)\cdot\Phi(z)+b)\\ {}\\ sign(\sum_{i-1}^{n}\lambda_iy_i(x_i \cdot z+1)^2+b) f(z)=sign(i=1∑nλjyjΦ(xi)⋅Φ(z)+b)sign(i−1∑nλiyi(xi⋅z+1)2+b)
4.Mercer定理
Mercer定理 核函数K可以表示为:
K ( u , v ) = Φ ( u ) ⋅ Φ ( v ) 当 前 仅 当 对 于 任 意 满 足 ∫ g ( x ) 2 d x 为 极 限 值 的 函 数 g ( x ) , 则 ∫ K ( x , y ) g ( x ) g ( y a ) d x d y ≥ 0 K(u,v)=\Phi(u)\cdot\Phi(v)\\ 当前仅当对于任意满足\int g(x)^2 dx 为极限值的函数g(x),则\\ {}\\ \int K(x,y)g(x)g(ya)dx dy \ge 0 K(u,v)=Φ(u)⋅Φ(v)当前仅当对于任意满足∫g(x)2dx为极限值的函数g(x),则∫K(x,y)g(x)g(ya)dxdy≥0
满足上述定理的核函数称为正定核函数,下面给出了一些核函数的例子:
K ( x , y ) = ( x ⋅ y + 1 ) p K ( x , y ) = e − ∣ ∣ x − y ∣ ∣ 2 / ( x σ 2 ) K ( x , y ) = t a n h ( k x ⋅ y − σ ) K(x,y)=(x\cdot y+1)^p\\ {}\\ K(x,y)=e^{-||x-y||^2/(x\sigma^2)}\\ {}\\ K(x,y)=tanh(kx \cdot y - \sigma) K(x,y)=(x⋅y+1)pK(x,y)=e−∣∣x−y∣∣2/(xσ2)K(x,y)=tanh(kx⋅y−σ)
- 代码
from sklearn import svm
X = [[0,0],[1,1]]
y = [0,1]
clf = svm.SVC(gamma='auto')
clf.fit(X,y)
# 预测新的值:
clf.predict([[2,2]])
- 输出
array([1])
5.6 组合方法
前面的几种分类方法,都是单一的分类器,这节介绍他们的组合方法。即将多个分类器组合到一起。
5.6.1组合方法的基本原理(略)
5.6.2构建组合分类器的方法
- (1)通过处理训练数据集
- 装袋
- 提升
- (2)通过处理输入特征
- 随机森林
- (3)通过处理类标号
5.6.3 偏倚-方差分解
考察组合方法的预测误差:
d f , θ ( y , t ) = B i a s θ + V a r i a n c e f + N o i s e t d_{f,\theta}(y,t)=Bias_{\theta}+Variance_f+Noise_t df,θ(y,t)=Biasθ+Variancef+Noiset
5.6.4 装袋
装袋(bagging)又称为自助聚集(boot strap aggregating),装袋的主要思想是根据均匀分布从数据中又放回的重复抽样,每个自主样本集和原数据集一样大。基于自主样本集通过基分类器进行分类,使用基分类器在不同的自主样本集中进行分类,对于每一个sample我们采取投票(Vote)的方式。该sample的类标签就是的票的最多的类标签。
- 例子
原始的基分类器:
| x | 0.1 | 0.2 | 0.03 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 1 | 1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 |
观察上面分类器的分类情况,最佳的决策点为 x ≤ 0.35 x\leq0.35 x≤0.35或者 x ≤ 0.75 x\leq0.75 x≤0.75,无论选择哪一个,树的准确率最多为70%。
假设我们在数据集上应用10个自主样本集的装袋过程,这样分类产生10个分类结果。

因为装袋过程是有放回的均匀分布抽样进行分类,所以在单轮中,有的并没有被抽中,而有的则被抽了多次。
然后,对上面的结果进行投票统计:
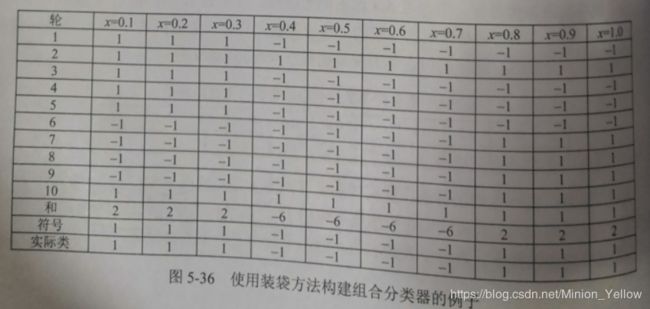
使用装袋后的分类器,准确率达到了100%。
但是装袋过程基于基分类器的稳定性,如果基分类器是不稳定的,装袋过程有助于改善泛化能力,但是如果基分类是稳定的,这时候分类器的误差主要来源于偏倚,此时装袋并不能苟有效的改善误差。
而且,因为时均匀分布装袋过程并不侧于训练数据集中的任何特定的实例,
5.6.5 提升(boosting)
提升是一个迭代的过程,用来自适应的改变寻览样本的分布,使得基分类器聚焦在那些很难分类的样本,提升给每一个训练样本赋予一个权值,而且每一轮提升过程结束时都自动的调整权值,训练样本的权值可以用于以下方面:
-
(1)可以作抽样分布,从原始数据集中抽取出自主样本集
-
(2)基分类器可以使用权值嘘唏有利于高权值样本的模型
-
例子
| 提升(第一轮) | 7 | 3 | 2 | 8 | 7 | 9 | 4 | 10 | 6 | 3 |
|---|---|---|---|---|---|---|---|---|---|---|
| 提升(第二轮) | 5 | 4 | 9 | 4 | 2 | 5 | 1 | 7 | 4 | 2 |
| 提升(第二轮) | 4 | 4 | 8 | 10 | 4 | 5 | 4 | 6 | 3 | 4 |
假设在该例子中,提升的第一轮中假设4很难分类,所以在第二轮和第三轮提升过程中加大了4的权重,所以分类器用于4的注意就多了
已经有需要不同的算法是实现提升,不同的算法的主要差别在于:
- (1)每轮提升结束时如何跟新样本的权值
- (2)如何组合每个分类器的预测
AdaBoost
令 { ( x j , y j ) ∣ j = 1 , 2 , . . . , N } \{(x_j,y_j)|j=1,2,...,N\} {(xj,yj)∣j=1,2,...,N}表示包含N个训练样本的集合。在Adaboost算法中,基分类器 C i C_i Ci的重要性依赖于它的错误率。错误率 ε i \varepsilon_i εi定义为:
ε i = 1 N ∑ j = 1 N w j I ( C i ( x j ) ≠ y i ) \varepsilon_i=\frac{1}{N}\sum_{j=1}^{N}w_j I(C_i(x_j)\not=y_i) εi=N1j=1∑NwjI(Ci(xj)=yi)
基分类器的 C i C_i Ci重要性由如下参数给出:
α i = 1 2 l n ( 1 − ε i ε ) \alpha_i = \frac{1}{2}ln(\frac{1-\varepsilon_i}{\varepsilon}) αi=21ln(ε1−εi)
如果错误率接近0, α i \alpha_i αi是一个很大的正值,当错误率接近1时, α i \alpha_i αi是一个很大的负值
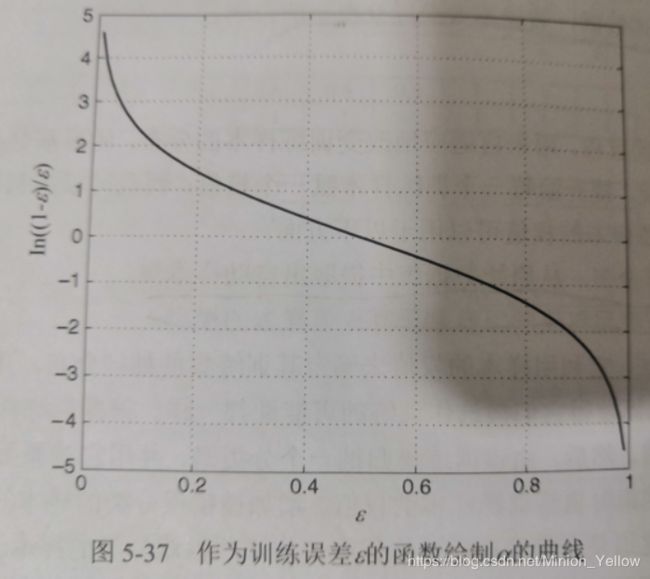
参数 α i \alpha_i αi可以被用来跟新训练样本的权值,假定 w i ( j ) w_i^(j) wi(j)表示在第j轮提升迭代中赋给样本 ( x i , y i ) (x_i,y_i) (xi,yi)的权值。AdaBoost的权值更新机制由下式给出:
w i ( j + 1 ) = w i ( j ) Z j × { e − α j 如 果 C j ( x i ) = y i e − α j 如 果 C j ( x i ) ≠ y i w_i^(j+1)=\frac{w_i^(j)}{Z_j} \times \begin{cases} e^{-\alpha_j} 如果C_j(x_i)=y_i\\ e^{-\alpha_j} 如果C_j(x_i) \not=y_i \end{cases} wi(j+1)=Zjwi(j)×{e−αj如果Cj(xi)=yie−αj如果Cj(xi)=yi
5.6.6 随机森林
随机森林是专门为决策树分类器涉及的组合方法,与AdaBoost不同,AdaBoost中的概率分布是变化的,而随机森林则采用一个固定的概率分布来产生随机向量。使用决策树装袋是随机森林的特例,通过随机地从原训练集中有放回地选取N个样本,将随机性加入到构建模型的过程中。整个模型的构建过程中,装袋也使用同样的均匀概率分布来产生它的自助样本。
- 代码实现
%matplotlib inline
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
# 实例化
# 训练 fit
# 导入测试集,score,Y_test
x_train,x_test,ytrain,ytest = train_test_split(wine.data,wine.target,test_size=0.3)
clf = DecisionTreeClassifier(random_state=0)
rfc = RandomForestClassifier(random_state=0)
clf = clf.fit(x_train,ytrain)
rfc = rfc.fit(x_train,ytrain)
score_c = clf.score(x_test,ytest)
score_r = rfc.score(x_test,ytest)
print("Single Tree{}".format(score_c)
,"Random.Forest:{}".format(score_r))
- 输出
Single Tree0.9259259259259259 Random.Forest:0.9814814814814815
5.7 不平衡类的问题
例如:
- 合格产品检验问题:不合格的产品的数量远远低于合格产品的数量
- 信用检测:合法交易远远多于欺诈交易
5.7.1 可选度量
由于准确率度量将每个类看的同等重要,因此它不适合来分析不平恒数据集。
对于二元分类,稀有类通常记为正类,多数类被记为负类。
- 混淆矩阵
| 预测的类 | |||
|---|---|---|---|
| + | - | ||
| 实际的类 | + | f_++(TP) | f_+- (FN) |
| - | f_-+(FP) | f_--(TN) | |
- 精度/准确率:
p = T P T P + F P p=\frac{TP}{TP+FP} p=TP+FPTP - 召回率:
r = T P T P + F N r=\frac{TP}{TP+FN} r=TP+FNTP
准确率和召回率不能同时减少,我们定义新的度量:F1
F 1 = 2 1 r + 1 p F_1=\frac{2}{\frac{1}{r}+\frac{1}{p}} F1=r1+p12
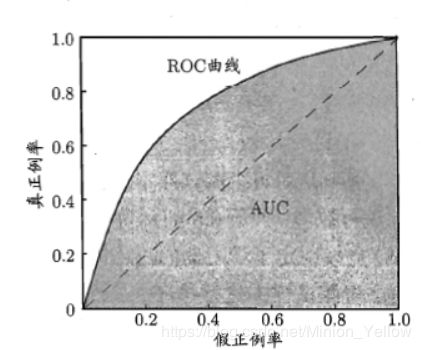
5.7.2 接收者操作特征曲线(ROC)
- TPR=0,FPR=0:把每个实例都预测为负类的模型
- TPR=1,FPR=1:把每个实例都预测为正类的模型
- TPR=1,FPR=0:理想模型
所以图片的左上角表示的是一个理想的模型。
5.7.3 代价敏感学习
模型的总代价定义为:
C t ( M ) = T P × C ( + , + ) + F P × C ( − , + ) + F N × C ( + , − ) + T N × C ( − , − ) C_t(M)=TP\times C(+,+) + FP \times C(-,+) + FN \times C(+,-) + TN \times C(-,-) Ct(M)=TP×C(+,+)+FP×C(−,+)+FN×C(+,−)+TN×C(−,−)
通过调整代价矩阵实现对不平衡数据的调整。
5.7.4 基于抽样的方法
假设有100个正样本和1000个负样本:
- 不充分抽样
* 对1000个负样本,抽取100个
* 问题:不能很好的获取负样本中的信息,解决方法:重复多次抽样(组合学习) - 过分抽样
* 复制100个正样本,直到和负样本一样多
* 问题:容易造成过拟合 - 混合方法
* 对多数类进行不充分抽样,对西游类进行过分抽样
5.8 多类问题
第一种方法(1-r):将多类问题分解为K个二类问题。为每一个类 y i ∈ Y y_i\in Y yi∈Y创建一个二类问题,其中所有属于 y i y_i yi的样本都被看成是正类,其他样本作为负类。
第二种方法(1-1):构建 K ( K − 1 ) 2 \frac{K(K-1)}{2} 2K(K−1)个二类分类器,每一个分类器用来区分一对类 ( y i , y j ) (y_i,y_j) (yi,yj).