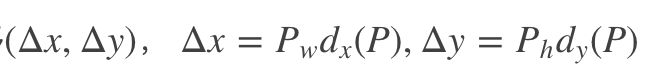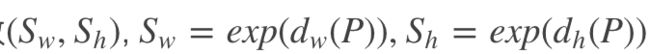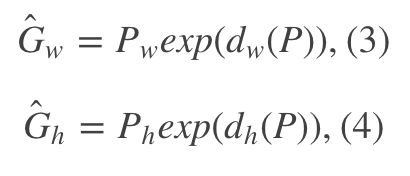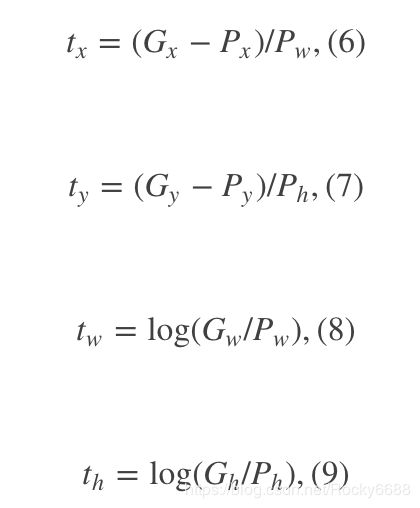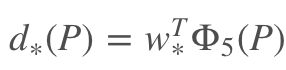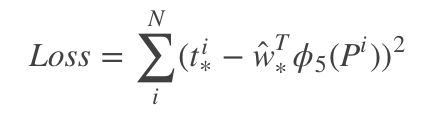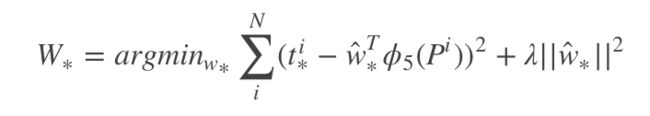深度学习_目标检测_边框回归(Bounding Box Regression)详解
为什么要边框回归?
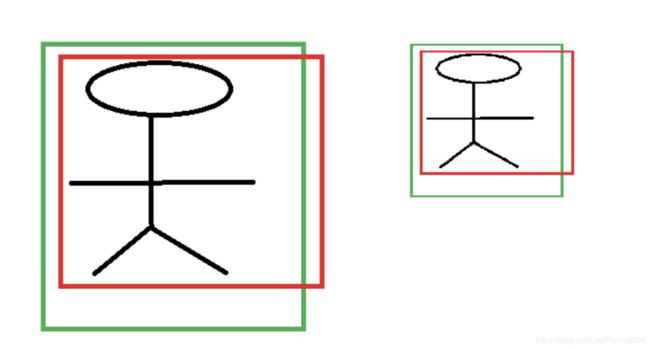
对于上图,绿色的框表示Ground Truth,红色的框为Selective Search提取的Region Proposal。那么即便红色的框被分类器识别为飞机,但是由于红色的框定位不准(IOU < 0.5),那么这张图相当于没有正确的检测出飞机。如果我们能对红色框进行微调,使得经过微调后的框跟Ground Truth更接近,这样岂不是定位会更准确。而Bounding-Box Regression就是用来微调这个框的。
边框回归是什么?
对于框一般使用四维向量 ( x , y , w , h ) (x, y, w, h) (x,y,w,h)来表示,分别是框的中心点坐标和宽高。对于下图所示的红色框P代表原始的Proposal,绿色的框G代表目标的Ground Truth,我们的目标是寻找一种关系使得输入原始的框P经过映射得到一个跟真实框G更接近的框 G ^ \hat{G} G^。
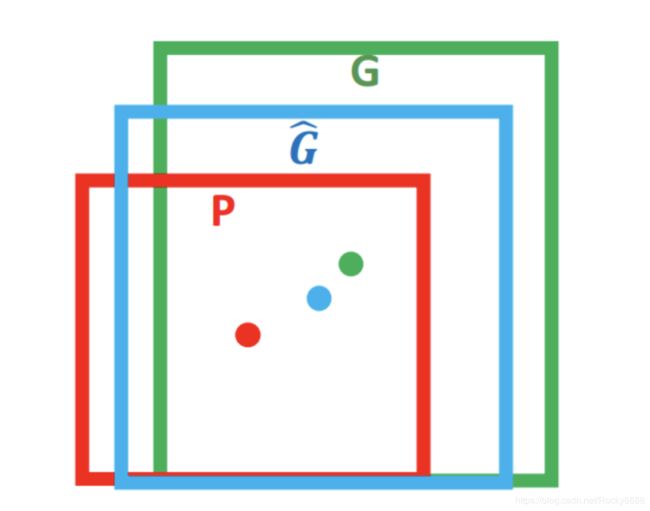
边框回归的目的既是:给定 ( P x , P y , P w , P h ) (P_{x}, P_{y}, P_{w}, P_{h}) (Px,Py,Pw,Ph)寻找一种映射 f f f,使得 f ( P x , P y , P w , P h ) = ( G x ^ , G y ^ , G w ^ , G h ^ ) f(P_{x}, P_{y}, P_{w}, P_{h}) = (\hat{G_{x}}, \hat{G_{y}}, \hat{G_{w}}, \hat{G_{h}}) f(Px,Py,Pw,Ph)=(Gx^,Gy^,Gw^,Gh^)并且 ( G x ^ , G y ^ , G w ^ , G h ^ ) ≈ ( G x , G y , G w , G h ) (\hat{G_{x}}, \hat{G_{y}}, \hat{G_{w}}, \hat{G_{h}}) \approx (G_{x}, G_{y}, G_{w}, G_{h}) (Gx^,Gy^,Gw^,Gh^)≈(Gx,Gy,Gw,Gh)
边框回归怎么做的?
那么经过何种变换才能从上图中框P变成框 G ^ \hat{G} G^呢?
比较简单的思路就是:平移 + 尺度缩放。
- 先做平移:
观察(1)- (4)我们可以发现,边框回归学习就是 d x ( P ) , d y ( P ) , d w ( P ) , d h ( P ) d_{x}(P), d_{y}(P), d_{w}(P), d_{h}(P) dx(P),dy(P),dw(P),dh(P)这四个变换。下一步就是设计算法得到这四个映射。
线性回归就是给定输入的特征向量X,学习一组参数W,使得经过线性回归后的值跟真实值Y(Ground Truth)非常接近,即 Y ≈ W X Y \approx WX Y≈WX。那么Bounding-box中我们的输入以及输出分别是什么呢?
Input
Output
那么目标函数也可以表示为:
其中 ϕ 5 ( P ) \phi_{5}(P) ϕ5(P)是输入Proposal的特征向量, W ∗ W_{*} W∗是要学习的参数(*表示x,y,w,h,也就是每一个变换对应一个目标函数)。 d ∗ ( P ) d_{*}(P) d∗(P)是得到的预测值。我们要让预测值跟真实值 t ∗ = ( t x , t y , t w , t h ) t_{*} = (t_{x}, t_{y}, t_{w}, t_{h}) t∗=(tx,ty,tw,th)差距最小,得到损失函数为:
我们利用梯度下降法或者最小二乘法就可以得到 W ∗ W_{*} W∗。
为什么宽高尺度会设计这种形式?
这边我重点解释一下为什么设计的 t x , t y t_{x}, t_{y} tx,ty要除以宽高,为什么 t w , t h t_{w}, t_{h} tw,th会有log形式。
首先CNN具有尺度不变形,如下图所示:
x,y坐标除以宽高
宽高坐标log形式
我们想要得到一个缩放的尺度,也就是说这里限制尺度必须大于0。我们学习的 t w , t h t_{w}, t_{h} tw,th怎么才能满足大于0呢?直观的想法就是EXP函数。如上面的公式(3),(4)所示。那么反过来推导就是log函数的来源了。
为什么IOU较大,认为是线性变换?
Reference
bounding box regression caffe社区