【TensorFlow】使用LeNet-5模型实现mnist手写数字识别

LeNet-5 模型

LeNet-5是卷积神经网络（CNN）中较简单的一个网络模型，在学习LeNet-5之前，最好先去了解以下卷积神经网络的基本概念与过程。

LeNet-5模型总共有7层，下图展示了LeNet-5模型的结构。

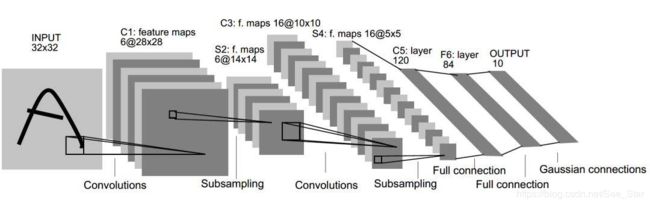
第一层：卷积层
输入为：32×32×1，由于过滤器尺寸为5×5，深度为6，步长为1，不使用全0填充。所以输出为：（32-5）÷1 +1=28，即28×28×6。本层有5×5×1×6+6=156个参数，由于下一层有28×28×6=4704个节点，每个节点和5×5=25个当前层节点相连，所以本层卷积层有4704×（25+1）=122304个连接。

第二层：池化层
输入为：28×28×6，采用过滤器大小为2×2，步长为2，所以输出为：（28-2）÷2+1=14，即14×14×6。

第三层：卷积层
输入为：14×14×6，由于过滤器尺寸为5×5，深度为16，步长为1，不使用全0填充。所以输出为：（14-5）÷1+1=10，即10×10×16。本层有5×5×6×16+16=2416个参数，有10×10×16×（5×5+1）=41600个连接。

第四层：池化层
输入为：10×10×16，采用过滤器大小为2×2，步长为2，所以输出为：（10-2）÷2+1=5，即5×5×16。

第五层：全连接层（卷积层）
输入为：5×5×16，如果将5×5×16矩阵节点拉成一个向量，本层输出节点个数：120，总共有5×5×16×120+120=48120个参数。

第六层：全连接层
输入节点个数为120个，输出节点个数为84个，总共有120×84+84=10164个。

第七层：全连接层
输入节点个数为84个，输出节点个数为10个，总共有84×10+10=850个。

通过TensorFlow的程序来实现一个类似LeNet-5模型的卷积神经网络来解决mnist数字识别问题。

代码

程序1：mnist_inference.py

该部分为LeNet-5的实现过程。

# -*- coding: utf-8 -*-
import tensorflow as tf

# 配置神经网络的参数
INPUT_NODE = 784  # 输入层的节点数。图像像素为24*24=784
OUTPUT_NODE = 10  # 输出层的节点数。等于类别的数目，0~9共10个数。

# 定义与样本数据相关的参数
IMAGE_SIZE = 28
NUM_CHANNELS = 1
NUM_LABELS = 10

# 第一层卷积层的尺寸和深度
CONV1_DEEP = 32
CONV1_SIZE = 5

# 第二层卷积层的尺寸和深度
CONV2_DEEP = 64
CONV2_SIZE = 5

# 全连接层的节点个数
FC_SIZE = 512


def inference(input_tensor, train, regularizer):
    with tf.variable_scope('layer1-conv1'):
        conv1_weights = tf.get_variable("weight",
                                        [CONV1_SIZE, CONV1_SIZE, NUM_CHANNELS, CONV1_DEEP],
                                        # 参数一、二：过滤器得尺寸；参数三：当前层得深度；参数四：过滤器的深度
                                        initializer=tf.truncated_normal_initializer(stddev=0.1))

        conv1_biases = tf.get_variable("bias",
                                       [CONV1_DEEP],
                                       initializer=tf.constant_initializer(0.0))

        conv1 = tf.nn.conv2d(input_tensor,
                             conv1_weights,
                             strides=[1, 1, 1, 1],  # 1、4位置固定为1；2、3位为不同维度上的步长，通常为1
                             padding='SAME')  # SAME表示添加0填充；VALID表示不添加
        relu1 = tf.nn.relu(tf.nn.bias_add(conv1, conv1_biases))

    # 实现第二层池化层的前向传播过程。这里选用最大池化层，池化层过滤器的边长为2，
    # 使用全0填充且移动的步长为2。这一层的输入是上一层的输出，也就是28x28x32 #的矩阵。输出为14x14x32的矩阵。
    with tf.name_scope('layer2-pool1'):
        pool1 = tf.nn.max_pool(relu1,
                               ksize=[1, 2, 2, 1],
                               strides=[1, 2, 2, 1],
                               padding='SAME')

    # 声明第三层卷积层的变量并实现前向传播过程。这一层的输入为14x14x32的矩阵。输出为14x14x64的矩阵。
    # 通过tf.get_variable的方式创建过滤器的权重变量和偏置项变量。
    with tf.variable_scope('layer3-conv2'):
        conv2_weights = tf.get_variable("weight",
                                        [CONV2_SIZE, CONV2_SIZE, CONV1_DEEP, CONV2_DEEP],
                                        initializer=tf.truncated_normal_initializer(stddev=0.1))
        conv2_biases = tf.get_variable("bias",
                                       [CONV2_DEEP],
                                       initializer=tf.constant_initializer(0.0))

        conv2 = tf.nn.conv2d(pool1,
                             conv2_weights,
                             strides=[1, 1, 1, 1],
                             padding='SAME')
        relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_biases))

    with tf.name_scope('layer4-pool2'):
        pool2 = tf.nn.max_pool(relu2,
                               ksize=[1, 2, 2, 1],
                               strides=[1, 2, 2, 1],
                               padding='SAME')

    pool_shape = pool2.get_shape().as_list()
    nodes = pool_shape[1] * pool_shape[2] * pool_shape[3]
    # 通过tf.reshape函数将第四层的输出编程一个batch的向量
    reshaped = tf.reshape(pool2, [pool_shape[0], nodes])

    # 声明第五层全连接层的变量并实现前向传播过程。这一层的输入是拉直之后的一组向量，
    # 向量长度为3136，输出是一组长度为512的向量。此处引入了 dropout的概念。
    # dropout在训练时会随机将部分节点的输出改为0。dropout可以避免过拟合问题，从而使得模型在测试数据上的效果更好。
    # dropout一般只在全连接层而不是卷积层或者池化层使用。
    with tf.variable_scope('layer5-fc1'):
        fc1_weights = tf.get_variable("weight",
                                      [nodes, FC_SIZE],
                                      initializer=tf.truncated_normal_initializer(stddev=0.1))

        # 只有全连接层的权重需要加入正则
        # 当给出了正则化生成函数时，将当前变量的正则化损失加入名字为losses的集合。
        # 在这里使用了add_to_collection函数将一个张量加入一个集合，而这个集合的名称为losses。
        if regularizer != None:
            tf.add_to_collection('losses', regularizer(fc1_weights))

        fc1_biases = tf.get_variable("bias",
                                     [FC_SIZE],
                                     initializer=tf.constant_initializer(0.1))
        fc1 = tf.nn.relu(tf.matmul(reshaped, fc1_weights) + fc1_biases)
        if train: fc1 = tf.nn.dropout(fc1, 0.5)

    # 声明第六层全连接层的变量并实现前向传播过程。这一层的输入为一组长度为512的向量，
    # 输出为一组长度为10的向量。这一层的输出通过Softmax之后就得到了最后的分类结果。
    with tf.variable_scope('layer6-fc2'):
        fc2_weights = tf.get_variable("weight",
                                      [FC_SIZE, NUM_LABELS],
                                      initializer=tf.truncated_normal_initializer(stddev=0.1))

        if regularizer != None:
            tf.add_to_collection('losses', regularizer(fc2_weights))

        fc2_biases = tf.get_variable("bias",
                                     [NUM_LABELS],
                                     initializer=tf.constant_initializer(0.1))
        logit = tf.matmul(fc1, fc2_weights) + fc2_biases

    return logit

程序2：mnist_train.py

该部分为模型的训练函数，需要自行更改模型的保持目录以及模型的名称。

# -*- coding: utf-8 -*-

import tensorflow as tf
import numpy as np

from tensorflow.examples.tutorials.mnist import input_data

# 加载mnist_inference.py中定义的常量和前向传播的函数
import mnist_inference

# 配置实现指数衰减学习率的相关参数
BATCH_SIZE = 100  # 数字越小时，训练过程越接近随机梯度下降；数字越大时，训练越接近梯度下降
LEARNING_RATE_BASE = 0.01  # 基础的学习率
LEARNING_RATE_DECAY = 0.99  # 学习率的衰减系数

# 配置实现正则化的相关参数
REGULARAZTION_RATE = 0.0001  # 正则化项的权重

# 配置实现滑动平均模型的相关参数
MOVING_AVERAGE_DECAY = 0.99  # 滑动平均模型的衰减率

# 迭代次数
TRAINING_STEPS = 8000


def train(mnist):
    """
    定义输入输出placeholder，其中mnist_inference.INPUT_NODE为784，mnist_inference.OUTPUT_NODE为10。
    TensorFlow提供了tf.contrib.layers.l2_regularizer函数，它可以返回一个函数，
    这个函数可以计算一个给定参数的l2正则化项的值。类似的，
    tf.contrib.layers.l1_regularizer可以计算L1正则化项的值
    """
    # 调整输入数据placeholder的格式，输入为一个四维矩阵。第一维表示一个batch中样例的个数；
    # 第二维和第三维表示图片的尺寸；第四维表示图片的深度，对于RBG格式的图片，深度为5。
    x = tf.placeholder(tf.float32, [BATCH_SIZE,
                                    mnist_inference.IMAGE_SIZE,
                                    mnist_inference.IMAGE_SIZE,
                                    mnist_inference.NUM_CHANNELS], name='x-input1')

    y_ = tf.placeholder(tf.float32, [None, mnist_inference.OUTPUT_NODE], name='y-input')

    regularizer = tf.contrib.layers.l2_regularizer(REGULARAZTION_RATE)  # 返回一个可以计算l2正则化项的函数

    y = mnist_inference.inference(x, True, regularizer)
    # 直接使用mnist_inference.py中定义的前向传播过程

    global_step = tf.Variable(0, trainable=False)
    # 定义存储训练轮数的变量，这个变量不需要计算滑动平均值，所以这里指定这个变量为不可训练的变量(trainable=False)。
    # 在使用tensorflow训练神经网络时，一般会将代表训练轮数的变量指定为不可训练的参数

    variable_averages = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)
    # 给定滑动平均衰减率和训练轮数的变量，初始化滑动平均类，ExponentialMovingAverage还提供了num_updates参数
    # 来动态设置decay的大小，因此，通过给定训练轮数的变量可以加快训练早期变量的更新速度

    variables_averages_op = variable_averages.apply(tf.trainable_variables())
    # 在所有代表神经网络参数的变量上使用滑动平均。其他辅助变量（比如global_step ）就不需要了。
    # tf.trainable_variables()返回的就是图上集合GraphKeys.TRAINABLE_VARIABLES中的元素。
    # 这个集合的元素就是所有没有指定trainable=False的参数

    cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
    # 因为交叉熵一般会与softmax回归一起使用，所以TensorFlow对这两个功能进行了统一封装，
    # 并提供了tf.nn.softmax_cross_entropy_with_logits函数。比如：
    # cross_entropy = tf.nn.softmax_cross_entropy_with_logits（y,y_），其中y代表了原始神经网络的输出结果，而y_代表标准答案。
    # 这样通过一个命令就可以得到使用了softmax回归之后的交叉熵。在只有一个正确答案的分类问题中，TensorFlow还提供了
    # tf.nn.sparse_softmax_cross_entropy_with_logits函数来进一步加速计算过程。
    # 注意，tf.argmax(vector, axis=1)，其中axis：0表示按列，1表示按行。返回的是vector中的最大值的索引号，
    # 如果vector是一个向量，那就返回一个值，如果是一个矩阵，那就返回一个向量，
    # 这个向量的每一个元素都是相对应矩阵行的最大值元素的索引号。

    cross_entropy_mean = tf.reduce_mean(cross_entropy)
    loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))
    # get_collection返回一个列表，这个列表包含所有这个losses集合中的元素，这些元素就是损失函数的不同部分，
    # 将它们加起来就可以得到最终的损失函数。
    # 其中tf.add_n([p1, p2, p3....])函数是实现一个列表的元素的相加。输入的对象是一个列表，列表里的元素可以是向量、矩阵等

    learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE,
                                               global_step,
                                               mnist.train.num_examples / BATCH_SIZE,
                                               LEARNING_RATE_DECAY,
                                               staircase=True)
    train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
    # 通过exponential_decay函数生成学习率，使用呈指数衰减的学习率，
    # 在minimize函数中传入global_step将自动更新global_step参数，从而使得学习率learning_rate也得到相应更新。

    with tf.control_dependencies([train_step, variables_averages_op]):
        train_op = tf.no_op(name='train')
    # 在训练神经网络模型时，每过一遍数据既需要通过反向传播来更新神经网络中的参数，
    # 又要更新每一个参数的滑动平均值。为了一次完成多个操作，TensorFlow提供了tf.control_dependencies机制

    saver = tf.train.Saver()
    # 初始化TensorFlow持久化类

    with tf.Session() as sess:
        # 初始化所有变量
        init_op = tf.global_variables_initializer()
        sess.run(init_op)

        # 在训练过程中不再测试模型在验证数据上的表现，验证和测试的过程将会有一个独立的程序来完成。
        print("*************开始训练*************")
        for i in range(TRAINING_STEPS):
            xs, ys = mnist.train.next_batch(BATCH_SIZE)

            # 类似地将输入的训练数据格式调整为一个四维矩阵,并将这个调整后的数据传入sess.run过程
            reshaped_xs = np.reshape(xs, (BATCH_SIZE,
                                          mnist_inference.IMAGE_SIZE,
                                          mnist_inference.IMAGE_SIZE,
                                          mnist_inference.NUM_CHANNELS))
            train_op_renew, loss_value, step = sess.run([train_op, loss, global_step],
                                                        feed_dict={x: reshaped_xs, y_: ys})
            if i % 1000 == 0:
                # 每1000轮保存一次模型。
                # 输出当前的训练情况。这里只输出了模型在当前训练batch上的损失函数大小。
                # 通过损失函数的大小可以大概了解训练的情况。
                # 在验证数据集上的正确率信息会有一个单独的程序来生成。
                print("After " + str(step) + " training step, loss on training batch is " + str(loss_value))

                saver.save(sess, r"E:\Python\deeplearning\LeNet-5\mode1.ckpt", global_step=global_step)
                # 持久化一个简单的tensorflow模型。注意这里给出了global_step参数，这样可以让每个被
                # 保存模型的文件名末尾加上训练的轮数，比如“model.ckpt-1000” 表示训练1000轮之后得到的模型。
                # 通过 saver.save函数将tensorflow模型保存到了C:\Users\Administrator\Desktop\code\tensorflow\model\
                # model.ckpt文件中。每次保存操作会生成三个文件，这是因为tensorflow会将计算图的结构和图上参数取值分开保存。
                # 第一个文件为model.ckpt.meta，它保存了tensorflow计算图的结构；第二个文件为model.ckpt，这个文件中保存了
                # tensorflow程序中每一个变量的取值；最后一个文件为checkpoint文件，这个文件中保存了一个目录下所有的模型文件列表。

        print("*******************训练结束*******************")


# 主程序入口
def main(argv=None):
    """
    主程序入口
    声明处理MNIST数据集的类，这个类在初始化时会自动下载数据
    """
    mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
    if mnist != None:
        print("*************数据加载完毕*************")
    train(mnist)


# TensorFlow提供的一个主程序入口，tf.app.run会调用上面定义的main函数
if __name__ == '__main__':
    tf.app.run()

运行结果：
（由于我是在gpu环境下使用的tensorflow，所以红字部分是gpu的相关信息，可忽略）

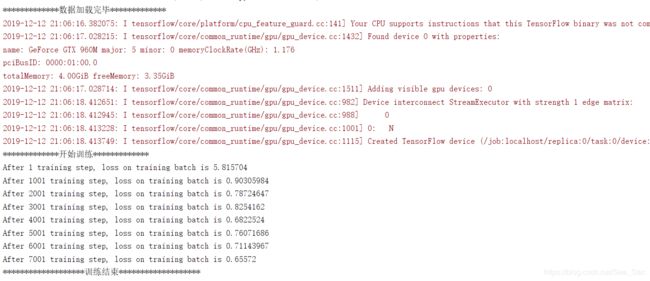
程序3：mnist_eval.py

该代码用于测试模型准确率，需要修改模型所在的目录，只要模型的目录即可，不需要模型的名称。

程序2保存模型的目录为（包含模型的名称）：E:\Python\deeplearning\LeNet-5\mode1.ckpt
程序3调用模型的目录为（不包含模型的名称）：E:\Python\deeplearning\LeNet-5

# -*- coding: utf-8 -*-

import time
import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data

# 加载mnist_inference.py和mnist_train.py中定义的常量和前向传播的函数
import mnist_inference
import mnist_train

# 每10秒加载一次最新的模型，并在测试数据上测试最新模型的正确率
EVAL_INTERVAL_SECS = 10


def evaluate(mnist):
    with tf.Graph().as_default() as g:  # 将默认图设为g
        # 定义输入输出的格式
        x = tf.placeholder(tf.float32, [mnist.validation.images.shape[0],
                                        mnist_inference.IMAGE_SIZE,
                                        mnist_inference.IMAGE_SIZE,
                                        mnist_inference.NUM_CHANNELS], name='x-input1')
        y_ = tf.placeholder(tf.float32, [None, mnist_inference.OUTPUT_NODE], name='y-input')

        xs = mnist.validation.images
        # 类似地将输入的测试数据格式调整为一个四维矩阵
        reshaped_xs = np.reshape(xs, (mnist.validation.images.shape[0],
                                      mnist_inference.IMAGE_SIZE,
                                      mnist_inference.IMAGE_SIZE,
                                      mnist_inference.NUM_CHANNELS))
        validate_feed = {x: reshaped_xs, y_: mnist.validation.labels}

        # 直接通过调用封装好的函数来计算前向传播的结果
        # 测试时不关注过拟合问题，所以正则化输入为None
        y = mnist_inference.inference(x, None, None)

        # 使用前向传播的结果计算正确率，如果需要对未知的样例进行分类
        # 使用tf.argmax(y, 1)就可以得到输入样例的预测类别
        correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
        # 首先将一个布尔型的数组转换为实数，然后计算平均值
        # 平均值就是网络在这一组数据上的正确率
        # True为1，False为0
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

        # 通过变量重命名的方式来加载模型
        variable_averages = tf.train.ExponentialMovingAverage(mnist_train.MOVING_AVERAGE_DECAY)
        variable_to_restore = variable_averages.variables_to_restore()
        # 所有滑动平均的值组成的字典，处在/ExponentialMovingAverage下的值
        # 为了方便加载时重命名滑动平均量，tf.train.ExponentialMovingAverage类
        # 提供了variables_to_store函数来生成tf.train.Saver类所需要的变量
        saver = tf.train.Saver(variable_to_restore)  # 这些值要从模型中提取

        # 每隔EVAL_INTERVAL_SECS秒调用一次计算正确率的过程以检测训练过程中正确率的变化
        # while True:
        for i in range(2):  # 为了降低个人电脑的压力，此处只利用最后生成的模型对测试数据集做测试
            with tf.Session() as sess:
                # tf.train.get_checkpoint_state函数
                # 会通过checkpoint文件自动找到目录中最新模型的文件名
                ckpt = tf.train.get_checkpoint_state('E:\Python\deeplearning\LeNet-5')     # 文件夹即可
                if ckpt and ckpt.model_checkpoint_path:
                    # 加载模型
                    saver.restore(sess, ckpt.model_checkpoint_path)
                    # 得到所有的滑动平均值
                    # 通过文件名得到模型保存时迭代的轮数
                    global_step = ckpt.model_checkpoint_path.split('-')[-1]
                    accuracy_score = sess.run(accuracy, feed_dict=validate_feed)  # 使用此模型检验
                    # 没有初始化滑动平均值，只是调用模型的值，inference只是提供了一个变量的接口，完全没有赋值
                    print("After %s training steps, validation accuracy = %g" % (global_step, accuracy_score))
                else:
                    print("No checkpoint file found")
                    return
                time.sleep(EVAL_INTERVAL_SECS)
                # time sleep()函数推迟调用线程的运行，可通过参数secs指秒数，表示进程挂起的时间。


def main(argv=None):
    mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
    evaluate(mnist)


if __name__ == '__main__':
    tf.app.run()

运行结果：
（红体字部分可忽略），模型的准确率可到到98.36%

参考
1 TensorFlow实战Google深度学习框架（第2版）
2 基于tensorflow和lenet-5模型实现mnist手写数字识别
3 mnist数据集在LeNet5卷积神经网络 学习总结