仿射变换及其变换矩阵的理解
博客:blog.shinelee.me | 博客园 | CSDN
文章目录
- 写在前面
- 仿射变换:平移、旋转、放缩、剪切、反射
- 变换矩阵形式
- 变换矩阵的理解与记忆
- 变换矩阵的参数估计
- 参考
写在前面
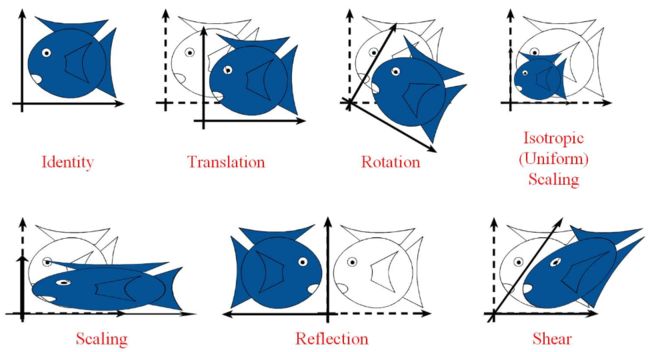
2D图像常见的坐标变换如下图所示:

这篇文章不包含透视变换(projective/perspective transformation),而将重点放在仿射变换(affine transformation),将介绍仿射变换所包含的各种变换,以及变换矩阵该如何理解记忆。
仿射变换:平移、旋转、放缩、剪切、反射
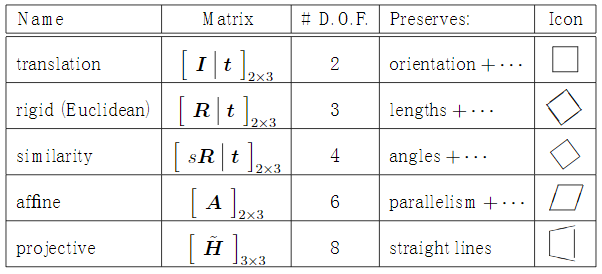
平移(translation)和旋转(rotation)顾名思义,两者的组合称之为欧式变换(Euclidean transformation)或刚体变换(rigid transformation);
放缩(scaling)可进一步分为uniform scaling和non-uniform scaling,前者每个坐标轴放缩系数相同(各向同性),后者不同;如果放缩系数为负,则会叠加上反射(reflection)——reflection可以看成是特殊的scaling;
刚体变换+uniform scaling 称之为,相似变换(similarity transformation),即平移+旋转+各向同性的放缩;
剪切变换(shear mapping)将所有点沿某一指定方向成比例地平移,语言描述不如上面图示直观。
各种变换间的关系如下面的venn图所示:
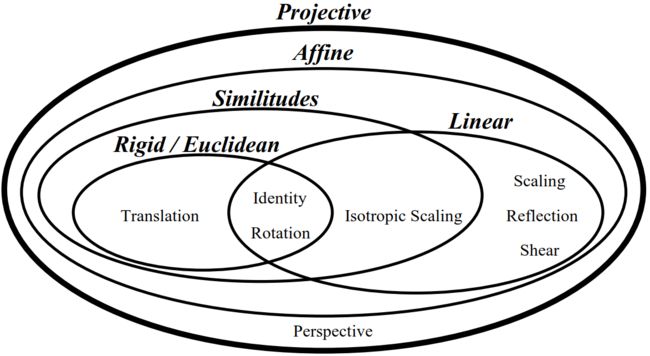
通过变换矩阵可以更清晰地看出这些变换间的关系和区别。
变换矩阵形式
没有平移或者平移量为0的所有仿射变换可以用如下变换矩阵描述:
[ x ′ y ′ ] = [ a b c d ] [ x y ] \left[ \begin{array}{l}{x'} \\ {y'}\end{array}\right]=\left[ \begin{array}{ll}{a} & {b} \\ {c} & {d}\end{array}\right] \left[ \begin{array}{l}{x} \\ {y}\end{array}\right] [x′y′]=[acbd][xy]
不同变换对应的 a , b , c , d a, b, c, d a,b,c,d约束不同,排除了平移变换的所有仿射变换为线性变换(linear transformation),其涵盖的变换如上面的venn图所示,其特点是原点位置不变,多次线性变换的结果仍是线性变换。
为了涵盖平移,引入齐次坐标,在原有2维坐标的基础上,增广1个维度,如下所示:
[ x ′ y ′ 1 ] = [ a b c d e f ] [ x y 1 ] \left[ \begin{array}{l}{x^{\prime}} \\ {y^{\prime}} \\ {1}\end{array}\right] =\left[ \begin{array}{lll}{a} & {b} & {c}\\ {d} & {e} & {f} \end{array}\right] \left[ \begin{array}{l}{x} \\ {y} \\ {1}\end{array}\right] ⎣⎡x′y′1⎦⎤=[adbecf]⎣⎡xy1⎦⎤
所以,仿射变换的变换矩阵统一用 [ a b c d e f ] \left[ \begin{array}{lll}{a} & {b} & {c}\\ {d} & {e} & {f}\end{array}\right] [adbecf]来描述,不同基础变换的 a , b , c , d , e , f a,b,c,d,e,f a,b,c,d,e,f约束不同,如下所示:
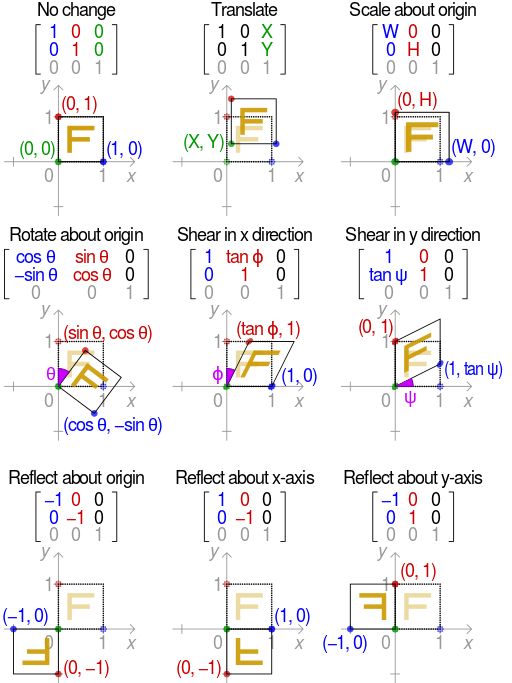
此外,旋转和平移相乘得到刚体变换的变换矩阵,如下,有3个自由度( θ , t x , t y \theta, t_x, t_y θ,tx,ty),这里旋转方向为逆时针方向,因此与上图中的正负号不同,
[ cos ( θ ) − sin ( θ ) t x sin ( θ ) cos ( θ ) t y ] [ x y 1 ] = [ x ′ y ′ 1 ] \left[ \begin{array}{ccc}{\cos (\theta)} & {-\sin (\theta)} & {t_{x}} \\ {\sin (\theta)} & {\cos (\theta)} & {t_{y}}\end{array}\right] \left[ \begin{array}{l}{x} \\ {y} \\ {1}\end{array}\right]=\left[ \begin{array}{c}{x^{\prime}} \\ {y^{\prime}} \\ {1}\end{array}\right] [cos(θ)sin(θ)−sin(θ)cos(θ)txty]⎣⎡xy1⎦⎤=⎣⎡x′y′1⎦⎤
再乘上uniform scaling得到相似变换,有4个自由度( s , θ , t x , t y s, \theta, t_x, t_y s,θ,tx,ty),如下:
[ s cos ( θ ) − s sin ( θ ) t x s sin ( θ ) s cos ( θ ) t y ] [ x y 1 ] = [ x ′ y ′ 1 ] \left[ \begin{array}{ccc}{s\cos (\theta)} & {-s\sin (\theta)} & {t_{x}} \\ {s\sin (\theta)} & {s\cos (\theta)} & {t_{y}}\end{array}\right] \left[ \begin{array}{l}{x} \\ {y} \\ {1}\end{array}\right]=\left[ \begin{array}{c}{x^{\prime}} \\ {y^{\prime}} \\ {1}\end{array}\right] [scos(θ)ssin(θ)−ssin(θ)scos(θ)txty]⎣⎡xy1⎦⎤=⎣⎡x′y′1⎦⎤
自然,仿射变换的变换矩阵有6个自由度( a , b , c , d , e , f a,b,c,d,e,f a,b,c,d,e,f)。
变换矩阵的理解与记忆

坐标系由坐标原点和基向量决定,坐标原点和基向量确定了,坐标系也就确定了。
对于坐标系中的位置 ( x , y ) (x, y) (x,y),其相对坐标原点在 [ 1 , 0 ] [1, 0] [1,0]方向上的投影为 x x x,在 [ 0 , 1 ] [0, 1] [0,1]方向上的投影为 y y y——这里投影的意思是过 ( x , y ) (x, y) (x,y)做坐标轴的平行线与坐标轴的交点到原点的距离,即 ( x , y ) (x, y) (x,y)实际为:
[ x y ] = x [ 1 0 ] + y [ 0 1 ] = [ 1 0 0 1 ] [ x y ] \left[ \begin{array}{l}{x} \\ {y}\end{array}\right] = x\left[ \begin{array}{l}{1} \\ {0}\end{array}\right] + y\left[ \begin{array}{l}{0} \\ {1}\end{array}\right] = \left[ \begin{array}{ll}{1} & {0} \\ {0} & {1}\end{array}\right] \left[ \begin{array}{l}{x} \\ {y}\end{array}\right] [xy]=x[10]+y[01]=[1001][xy]
当坐标系变化,坐标系中的点也跟着变化,但点相对新坐标系( x ′ − y ′ x'-y' x′−y′坐标系)的位置不变仍为 ( x , y ) (x, y) (x,y),以旋转变换为例,新坐标轴的基向量则变为 [ cos ( θ ) , sin ( θ ) ] [\cos (\theta), \sin (\theta)] [cos(θ),sin(θ)]和 [ − sin ( θ ) , cos ( θ ) ] [-\sin (\theta), \cos (\theta)] [−sin(θ),cos(θ)],所以点变化到新位置为:
[ x ′ y ′ ] = x [ cos ( θ ) sin ( θ ) ] + y [ − sin ( θ ) cos ( θ ) ] = [ cos ( θ ) − sin ( θ ) sin ( θ ) cos ( θ ) ] [ x y ] \left[ \begin{array}{l}{x'} \\ {y'}\end{array}\right] = x\left[ \begin{array}{l}{\cos (\theta)} \\ { \sin (\theta)}\end{array}\right] + y\left[ \begin{array}{r}{- \sin (\theta)} \\ { \cos (\theta)}\end{array}\right] = \left[ \begin{array}{lr}{\cos (\theta)} & {-\sin (\theta)} \\ {\sin (\theta)} & {\cos (\theta)}\end{array}\right] \left[ \begin{array}{l}{x} \\ {y}\end{array}\right] [x′y′]=x[cos(θ)sin(θ)]+y[−sin(θ)cos(θ)]=[cos(θ)sin(θ)−sin(θ)cos(θ)][xy]
新位置和新基向量是相对绝对坐标系( x − y x-y x−y坐标系)而言的。其他变换矩阵同理。
总结一下:
- 所有变换矩阵只需关注一点:坐标系的变化,即基向量和原点的变化;
- 坐标系变化到哪里,坐标系中的所有点也跟着做同样的变化;
- 坐标系的变换分为 基向量的变化 以及 坐标原点的变化,在仿射变换矩阵 [ a b c d e f 0 0 1 ] \left[ \begin{array}{lll}{a} & {b} & {c}\\ {d} & {e} & {f} \\ 0 & {0} & {1}\end{array}\right] ⎣⎡ad0be0cf1⎦⎤中, [ a d ] \left[ \begin{array}{l}{a} \\ {d}\end{array}\right] [ad]和 [ b e ] \left[ \begin{array}{l}{b} \\ {e}\end{array}\right] [be]为新的基向量, [ c f ] \left[ \begin{array}{l}{c} \\ {f}\end{array}\right] [cf]为新的坐标原点,先变化基向量,再变化坐标原点;
这时再对照上面的各种变换矩阵,就很好理解了。
变换矩阵的参数估计
如果给定两个对应点集,如何估计指定变换矩阵的参数?
一对对应点可以列两个线性方程,多个对应点可以列出线性方程组,为了求解参数,需要的对应点数至少为自由度的一半,多个点时构成超定方程组,可以基于最小二乘或者SVD分解等方法进行求解,这里不再展开。
参考
- Image Alignment and Stitching: A Tutorial
- wiki: Affine transformation
- Geometric Transformation
- Coordinates and Transformations
- Transformations
- Geometric Transformations
- Image Geometry