NLP(文本)中的对抗训练
《NLP中的对抗训练》
最近在做百度的阅读理解竞赛,这次的竞赛目的主要是针对模型的鲁棒性。百度提出了dureader-robustness数据集,具体可以参考之前的博客《Improving the Robustness of Question Answering Systems to Question Paraphrasing
》,有介绍到具体的问题和任务。
那么针对上述的问题,能用什么方法解决呢?
显而易见:
- 数据增强
- 对抗训练
数据增强就不用说了,着重介绍一下对抗训练
不同的文章对于对抗扰动的定义略有不同,但是一般来说对抗扰动具有两个特点:
-
扰动是微小的甚至是肉眼难以观测到的(图 1 中间部分);
-
添加的扰动必须有能力使得模型产生错误的输出(图 1 右侧部分)。

在文本处理中添加的扰动可以是离散的也可以是连续的,一般来说离散扰动指的是直接对输入文本字符进行微小修改(如图 2),连续扰动一般指的是直接在输入文本中的词向量矩阵中添加的扰动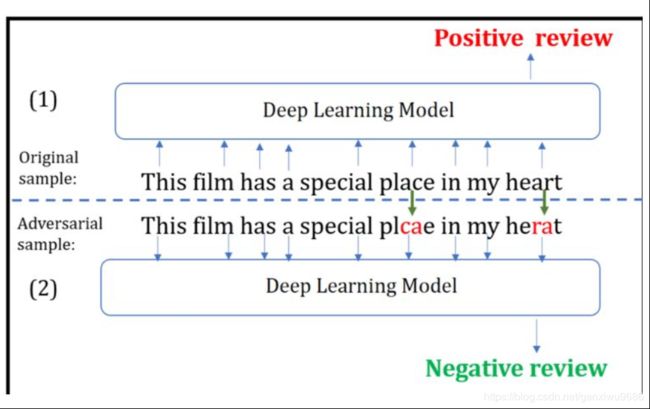
要求添加扰动后产生的对抗样本与原样本在语义上保持一致,即添加的扰动应该尽量不改变原始句子的语义。因此,需要一个测度来衡量扰动前后文本的差异。
余弦距离、欧式距离和 WMD 基于词向量计算,主要适用于连续扰动的情况,Jaccard 相似系数,编辑距离可以直接基于文本字符来计算,主要适用于离散扰动的情况。
为了满足对抗扰动的基本特征 2,常用的方法有基于梯度的方法 [3],直接优化的方法 [1] 等。其中基于梯度的方法一般是计算损失函数对于输入x的梯度dL/dx, 对计算的梯度进行相应变换(Goodfellow 2014. [3], Kurakin A, Goodfellow I 2016. [6], Carlini N, Wagner D. 2017. [7])从而产生扰动 r。
按攻击目的,可分为目标攻击和非目标攻击,目标攻击指的是生成的对抗样本希望被模型错分到某个特定的类别上。非目标攻击指的是对抗样本只要能让模型分错就行,不论错分到哪个类别都可以。本文主要阐述对抗攻击中的非目标攻击方法(接下来的内容主要参考自 [2])。
1、其中 Papernot et al. [8]首先开始研究文本序列中对抗样本的问题,提出了在递归神经网络(RNN)上产生对抗性输入序列。他们利用计算图展开 [9]来估算输入序列的正向导数 [10],即雅可比矩阵。然后对于输入的每个单词,在上述雅可比张量上使用快速梯度符号法(FGSM)[3]来计算得到扰动。
同时,为了解决修改后的词向量映射问题,他们构建了一个特殊的字典用以选择单词来替换原单词,其中,该替换操作有一个约束,就是替换前后的符号差异要最接近 FGSM 的结果。尽管对抗扰动输入序列可以使 LSTM 模型出现错误,但输入序列的单词是随机选择的,可能存在语法错误。
2、samanta et al.[11]引入了三个修改策略,即插入,替换和删除。在尽可能保留输入的语义的前提下,用这些策略生成对抗样本。这些修改策略针对的是那些如果删除后会对分类结果产生很大影响的重要单词。因此,作者利用 FGSM 来验证每一个单词在文本中的贡献,然后以贡献度的递减顺序来定位重要单词。
除了删除之外,插入和替换都需要包括同义词,拼写错误和流派特殊关键词在内的候选池来提供帮助。因此,在实验中,作者为每个单词建立了一个候选池。但是,这样会消耗大量时间,而且事实上,输入文本中很多最重要的单词可能没有候选池。
3、Gao et al.[12]提出了算法 DeepWordBug 用以误导 DNN 网络,不同于前面两者,DeepWordBug 适用于黑盒攻击的情境,算法分为两阶段,首先第一阶段是确定哪些重要的 token 要进行改变,第二阶段是产生难以被检测到的扰动。 第一阶段的计算过程如下:
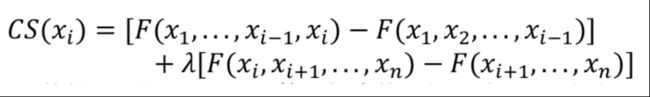
x i x_i xi 是输入的第 i 个单词,F 是计算置信度的函数。随后,类似如交换,替换,删除和插入等修改策略被应用于重要的 token,这样就得到更好的对抗样本。 同时,为了保持这些对抗样本的可读性,作者使用了编辑距离作为约束测度。
4、除了上述直接加在文本序列上的对抗扰动方法外,还可以通过在词向量上添加连续扰动的方式进行对抗攻击。Sato et al. [4]直接在 embedding 空间对输入文本上做手脚,用这种方法得到的对抗样本也可以对目标模型进行影响从而导致错误分类。这种方法的核心思想在于搜索最大化损失函数的方向向量权重,总体参数 W 如下:

其中,

是从每个输入词向量生成的扰动,是从 embedding 空间中一个词到另一个的词的方向向量。因为上式非常难以计算,因此作者用下式替代:

iAdvT 的损失函数定义为基于在整个训练数据集 D 上的优化问题,即最小化目标函数:
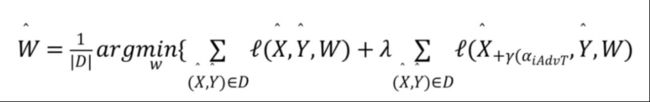
与 Miyato et al. [13] 对比,该方法限定了扰动的方向并以此找到预定义词表中的替代词而不是未知词来替换原词。 因此,它通过对抗性训练提高了对抗性例子的可解释性。 同时,作者还利用了余弦相似性来选择更好的扰动。
pytorch 实现:
Fast Gradient Method(FGM)
上面我们提到,Goodfellow 在 15 年的 ICLR [3] 中提出了 Fast Gradient Sign Method(FGSM),随后,在 17 年的 ICLR [16] 中,Goodfellow 对 FGSM 中计算扰动的部分做了一点简单的修改。假设输入的文本序列的 embedding vectors 为 x ,embedding 的扰动为:

import torch
class FGM(object):
def __init__(self, model):
super(FGM, self).__init__()
self.model = model
self.backup = {}
def attack(self, epsilon=1., emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
self.backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = epsilon * param.grad / norm
param.data.add_(r_at)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.backup
param.data = self.backup[name]
self.backup = {}
需要使用对抗训练的时候,只需要添加代码:
fgm = FGM(model)
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
# 对抗训练
fgm.attack() # 在embedding上添加对抗扰动
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
fgm.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
Projected Gradient Descent(PGD)
import torch
class PGD():
def __init__(self, model):
self.model = model
self.emb_backup = {}
self.grad_backup = {}
def attack(self, epsilon=1., alpha=0.3, emb_name='emb.', is_first_attack=False):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
if is_first_attack:
self.emb_backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = alpha * param.grad / norm
param.data.add_(r_at)
param.data = self.project(name, param.data, epsilon)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.emb_backup
param.data = self.emb_backup[name]
self.emb_backup = {}
def project(self, param_name, param_data, epsilon):
r = param_data - self.emb_backup[param_name]
if torch.norm(r) > epsilon:
r = epsilon * r / torch.norm(r)
return param_data + r
def backup_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
self.grad_backup[name] = param.grad
def restore_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
param.grad = self.grad_backup[name]
使用的时候:
pgd = PGD(model)
K = 3
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
pgd.backup_grad()
# 对抗训练
for t in range(K):
pgd.attack(is_first_attack=(t==0)) # 在embedding上添加对抗扰动, first attack时备份param.data
if t != K-1:
model.zero_grad()
else:
pgd.restore_grad()
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
pgd.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
reference
[1] C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. J. Goodfellow, and R. Fergus, “Intriguing properties of neural networks,” in Proceedings of the International Conference on Learning Representations, 2014.
[2] Wang, W., Wang, L., Tang, B., Wang, R., & Ye, A. (2019). A survey on Adversarial Attacks and Defenses in Text, 1–13. Retrieved from http://arxiv.org/abs/1902.07285
[3] I. J. Goodfellow, J. Shlens, and C. Szegedy, “Explaining and harnessing adversarial examples,” in Proceedings of the International Conference on Learning Representations, 2015.
[4] M. Sato, J. Suzuki, H. Shindo, and Y. Matsumoto, “Interpretable adversarial perturbation in input embedding space for text,” in International Joint Conference on Artificial Intelligence (IJCAI), 2018.
[5] J. Gao, J. Lanchantin, M. L. Soffa, and Y. Qi, “Black-box generation of adversarial text sequences to evade deep learning classifiers,” in IEEE Security and Privacy Workshops (SPW). IEEE, 2018.
[6] Kurakin A, Goodfellow I, Bengio S. Adversarial examples in the physical world. arXiv preprint arXiv:1607.02533, 2016.
[7] Carlini N, Wagner D. Towards evaluating the robustness of neural networks//Security and Privacy (SP), 2017 IEEE Symposium on. IEEE, 2017: 39-57.
[8] N. Papernot, P. McDaniel, A. Swami, and R. Harang, “Crafting adversarial input sequences for recurrent neural networks,” in IEEE Military Communications Conference, 2016, p. 4954.
[9] P. J.Werbos, “Generalization of backpropagation with application to a recurrent gas market model,” Neural Networks, vol. 1, no. 4, pp. 339–356, 1988.
[10] N. Papernot, P. McDaniel, S. Jha, M. Fredrikson, Z. B. Celik, and A. Swami, “The limitations of deep learning in adversarial settings,” in IEEE European Symposium on Security and Privacy. IEEE, 2016.
[11] S. Samanta and S. Mehta, “Towards crafting text adversarial samples,” 2017, arXiv preprint arXiv:1707.02812.
[12] J. Gao, J. Lanchantin, M. L. Soffa, and Y. Qi, “Black-box generation of adversarial text sequences to evade deep learning classifiers,” in IEEE Security and Privacy Workshops (SPW). IEEE, 2018.
[13] T. Miyato, A. M. Dai, and I. Goodfellow, “Adversarial training methods for semi-supervised text classification,” in Proceedings of the International Conference on Learning Representations, 2017.
[14] Z. Gong, W. Wang, B. Li, D. Song, and W.-S. Ku, “Ad- versarial texts with gradient methods,” 2018, arXiv preprint arXiv:1801.07175.
[15] Singh Sachan, D., Zaheer, M., & Salakhutdinov, R. (2019). Revisiting LSTM Networks for Semi-Supervised Text Classification via Mixed Objective Function. Retrieved from www.aaai.org.
[16] Adversarial Training Methods for Semi-Supervised Text Classification
https://arxiv.org/abs/1605.07725
[17] https://blog.csdn.net/c9Yv2cf9I06K2A9E/article/details/103060037