深度学习基础算法-神经网络之激活函数
神经网络算法
神经网络算法试图模拟生物神经系统的学习过程,以此实现强大的预测性能。不过由于是模仿人类大脑,所以神经网络的模型复杂度很高也是众所周知。在现实应用中,神经网络可以说是解释性最差的模型之一,商业环境中很少使用神经网络。然而除了商业分析,还有许多算法应用的部分,其中最重要的是深度学习和人工智能的领域,现在大部分已经成熟的人工智能技术:图像识别,语音识别等等,背后都是基于神经网络的深度学习算法。因此,作为机器学习中(可能是)最复杂的,深度学习中基础的算法,神经网络的了解和学习是很有必要的。
从感知机到神经网络
神经网络与多层感知机还是有一点区别的。用图来表示神经网络的话,如下图所示。我们把最左边的一列称为输入层,最右边的一列称为输出层,中间的一列称为中间层(有的教材也称为隐藏层)。所谓"隐藏"的意思,在这里面的神经元我们是看不见的。我们把下图的三层依次称为第0层,第1层,第2层,分别对应输入层,中间层,输出层。

单就神经网络的这种连接方式,和之前的感知机是没有任何差别的。感知机的公式:

在之前的图片中,偏置 并没有在图像中显示出来,我们可以把图片改成下图来表示权重 ,它对应的输入信号固定为1。

这个感知机将x1 、x2、1 三个信号作为神经元的输入,将其和各自的权重相乘后,传送至下一个神经元。在下一个神经元中,计算这些加权信号的总和。如果这个总和超过0,则输出1,否则输出0。而偏置部分的信号始终是1,是不变的。现在,我们为了能够进一步简化公式,为之后使用线性代数计算更方便,我们把公式再一次进行改造:
y = h ( b + ω 1 x 1 + ω 2 x 2 ) y=h(b+ω_1x_1~+ω_2x_2) y=h(b+ω1x1 +ω2x2)
而h(x)就应该是这样的:
h ( x ) = { 0 x ⩽ 0 1 x ⩾ 0 h(x)=\left\{ \begin{array}{ll} 0 & x \leqslant 0\\1 & x \geqslant 0 \end{array} \right. h(x)={01x⩽0x⩾0
输入信号的总和会被函数h(x)转换,转换后的值就是输出y。这样一来我们就把之前的公式拆分成两个更简单的模式了。在感知机中,h(x) 这个函数的形式非常简单,就是当输入总和不超过0的时候,输出0,而输入总和超过0的时候,就输出1。这种h(x)函数,我们叫做阶跃函数,使用这种算法的感知机一般叫做"朴素感知机"。
但是,在神经网络也就是"多层感知机中"中,我们通常不会采用这么简单的函数,而会使用更复杂一些的 h(x) 决定到底是输出0还是1。
激活函数
我们为什么要费劲把公式拆分上上面的那种形式呢,就是为了激活函数的登场在做铺垫。h(x) 这个函数,会将输入信号的总和转换为输出信号(0或者1),我们把这种函数称为激活函数(activation function)。激活的意思就是,使用这个函数来判断,当输入进行的总和达到什么程度的时候才予以输出。
我们把刚才的感知机公式,再一次进行改造。因为h(x) 可以是其他的形式:
a = b + ω 1 x 1 + ω 2 x 2 y = h ( a ) a=b+ω_1x_1~+ω_2x_2\\ y=h(a) a=b+ω1x1 +ω2x2y=h(a)
首先,计算加权输入信号和偏置的总和,记为a。然后,用h(x)函数将a转换为输出y。如果我们想要在图中明确表示出上面两个公式的表示过程,可以把图片变成这样.

首先,计算加权输入信号和偏置的总和,记为a。然后,用h(x)函数将a转换为输出y。如果我们想要在图中明确表示出上面两个公式的表示过程,可以把图片变成这样.
信号的加权总和为节点a,然后节点a被激活函数h()转换成节点y。这里所说的"节点",和之前所说的"神经元"含义相同。
那么常用的激活函数有哪些呢?下面我们一起来看一下:

sigmoid函数
sigmoid函数是神经网络中最常使用的一个激活函数,如果学过逻辑回归的同学应该知道,在逻辑回归中我们也是使用这个函数去进行分类的。sigmoid函数的公式为:

这里的e是自然常数,值约为2.71828。向sigmoid函数输入某个数值后,例如5,8,3.4 等,sigmoid函数就会对应的输出一个值.
具体的结果,我们可以先画出sigmoid函数的图像.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# sigmoid函数
def sigmoid(x):
h = 1/(1+np.exp(-x))
return h
# 绘制 sigmoid函数曲线
x = np.arange(-10,10,0.1)
y = sigmoid(x)
plt.figure(figsize = (8,6),dpi=60)
plt.plot(x,y,c='blue',alpha=0.8,linewidth=2,label='Sigmoid line')
plt.ylim(-0.1,1.1)
plt.xlim(-11,11)
plt.yticks(np.arange(0,1.1,0.1),fontsize=12)
plt.xticks(np.arange(-10,11,2),fontsize=12)
plt.title('Sigmoid line Plot',color='k',fontsize=15)
plt.grid(linestyle='-.',alpha=0.4)
plt.legend(loc=2,frameon=False,fontsize=12)
plt.show()
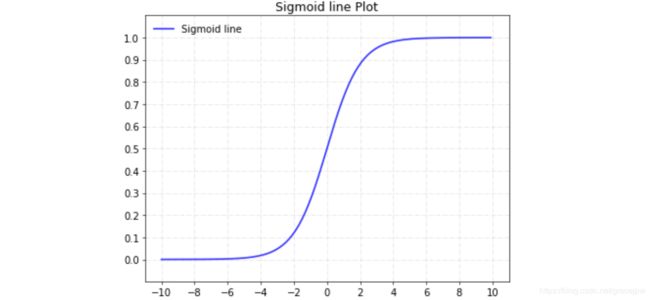
观察图形可以看到,sigmoid函数是一条平滑的,在0-1之间变化的曲线。为了说明sigmoid函数有什么样的好处,我们用感知机中的阶跃函数和sigmoid函数进行对比.
阶跃函数的实现
首先我们用Python实现这个函数的功能:
def step_function(x):
if x > 0:
return 1
else:
return 0
step_function(1)
1
如果输入的是Ndarray数组,则可以这样实现:
# 使用numpy实现阶跃函数
def step_function(x):
y = x > 0 #生成布尔序列
return y.astype(np.int) #把布尔序列转换成1和 0
对于这个函数,当我们传输一些数组的时候,会一次生成阶跃函数的正确结果
x = np.array([-1,1,2])
step_function(x)
array([0, 1, 1])
#比如:
np.array([True,False]).astype(np.int)
array([1, 0])
我们也可以画出阶跃函数的图像:
# 绘制阶跃函数图形
x = np.arange(-5,5,0.01)
y = step_function(x)
plt.plot(x,y);
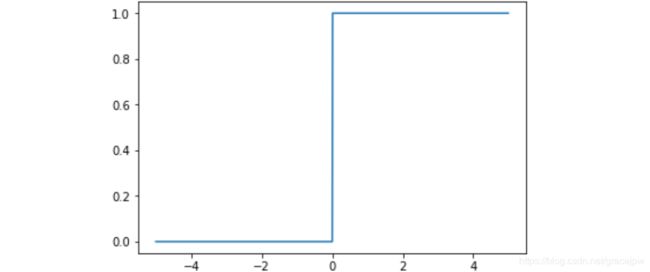
阶跃函数以0为界,输出从0切换为1(或者从1切换为0),它的值呈阶梯式变化,所以称为阶跃函数。
sigmoid函数和阶跃函数的比较
首先,最明显的是函数的平滑性不同,sigmoid是一条平滑连续的曲线,而阶跃函数以0为界,在这里输出发生根本性变化。而神经网络的学习,我们需要的不是非此即彼的变化,而是平滑的变化形式,因此sigmoid函数这种平滑的特点对于神经网络具有重要意义。

另一个不同点是,相对于阶跃函数只能返回0或1,sigmoid函数可以返回0.731 . . . 、0.880 . . . 等实数,当然这也是由平滑性决定的,如果神经网络中传递的信号,只有0和1的话,毫无疑问,这个网络的变化就太简单了,而sigmoid函数这种形式可以保证模型足够复杂的变化。也就是说,感知机中神经元之间流动的是0或1的二元信号,而神经网络中流动的是连续的实数值信号。
如果把这两个函数与水联系起来,则阶跃函数可以比作“竹筒敲石”,sigmoid函数可以比作“水车”。阶跃函数就像竹筒敲石一样,只做是否传送水(0或1)两个动作,而sigmoid函数就像水车一样,根据流过来的水量相应地调整传送出去的水量。
阶跃函数和sigmoid函数之间也是有共同点的:从图像上可以看出来,两者都是在0和1之间进行变化,当输入小的时候,输出为0或者接近0,当输入增大,输出就变成1或者接近1。也就是说,当输入信号为重要信息时,阶跃函数和sigmoid函数都会输出较大的值;当输入信号为不重要的信息时,两者都输出较小的值。还有一个共同点是,不管输入信号有多小,或者有多大,输出信号的值都在0到1之间。
非线性函数
阶跃函数和sigmoid函数还有其他共同点,就是两者均为非线性函数。sigmoid函数是一条曲线,阶跃函数是一条像阶梯一样的折线,两者都属于非线性的函数。神经网络的激活函数必须使用非线性函数。换句话说,激活函数不能使用线性函数。为什么不能使用线性函数呢?因为使用线性函数的话,加深神经网络的层数就没有意义了!
为了具体地(稍微直观地)理解这一点,我们来思考下面这个简单的例子:把线性函数h(x) = cx作为激活函数,把y(x) = h(h(h(x)))的运算对应3层神经网络,则
y ( x ) = h ( h ( h ( x ) ) ) = c ∗ c ∗ c x = 3 c x 令 α = 3 c , 则 有 : y ( x ) = α x y(x) =h(h(h(x)))\\=c*c*cx\\ =3cx\\ 令α=3c,则有:\\ y(x)=αx y(x)=h(h(h(x)))=c∗c∗cx=3cx令α=3c,则有:y(x)=αx
由于α和c都是常数,所以y(x)=αx与h(x)=cx是完全等价的。也就是说,对于线性函数来说,不管如何加深层数,总是存在与之等效的“无隐藏层的神经网络”。所以说,使用线性函数时,无法发挥多层网络带来的优势。因此,为了发挥叠加层所带来的优势,激活函数必须使用非线性函数。
ReLU 函数
作为激活函数,sigmoid函数在神经网络的发展历史上很早被应用,但是现在来讲,ReLU(Rectified Linear Unit) 修正线性单元函数应用会更加广泛一些。
ReLU函数具有这样的特性:输入大于0时,直接输出该值;在输入小于等于0时,输出0。ReLU的函数公式为:

ReLU函数是一个非常简单的函数,使用Python去实现的话,可以这样写:
def relu(x):
y = np.maximum(0,x)#从输入的数值中选择较大的那个值输出
return y
relu(-5)
0
绘制relu函数的图像:
# 绘制 relu函数
x = np.arange(-5,5,0.01)
y = np.maximum(0,x)
plt.plot(x,y);
