异常波动识别算法

张若雪：自动识别金融市场异常波动——机器学习的一个应用

2019-09-23  糖儿p7tz6...  转自 挑燈看劍r7w...

修改

打开今日头条，查看更多图片 文/中国人民银行上海总部张若雪 金融市场一直处于波动之中。大部分时间市场波动都是正常的，但有一些波动，源于突然发生的外部冲击或者未被预期的其它因素，从而表现出不同于正常模式的异常状态。这些异常波动，有一部分市场可以很快消化，另一部分则可能引发正反馈放大效应，单靠市场无形之手难以自拔，实体经济也将为此付出重大代价。近年来我国货币市场、股票市场都发生过类似情况。及时识别出异常波动，将其与正常波动区分开来，以在必要时迅速做出政策反应，是防范化解系统性金融风险的首要一步，在这方面机器学习可以发挥重要的作用。 本文以货币市场质押式回购交易为研究对象，利用IF（Isolation Forest）和LOD（Local OutlierFactor）两种算法训练机器学习模型，识别正常波动和异常波动。我们不主观地设定“正常”、“异常”的标准，而是由计算机按照算法，从历史数据中“学习”潜在的规律，判断什么是异常的波动。这样做优点主要有：一是大幅降低判断的主观性，由算法自动拟合潜在的决策函数，发现潜在的数据模式；二是适合处理大数据和多维数据，面对此类问题人脑受制于有限的记忆，以及难以理解多维空间；三是时效性强，随着时间的发展，数据分布很可能发生改变，判断标准也应随之调整，算法能够及时识别数据模式变化。 一、异常值识别的无监督学习算法 机器学习按照训练数据有无目标值，可以分为有监督学习和无监督学习。无监督学习是适用于没有目标值的训练数据的算法，目的是从训练集中学习“潜在”的决策函数，能够帮助人们发现潜在的规律性。用于识别异常值的无监督机器学习算法主要有四种，分别是One-Class SVM，Elliptic Envelope，Isolation Forest，Local Outlier Factor。 考虑这样一个问题：p维空间中有n个点，已知它们服从同一分布，如果现在观测到一个新的点，那么新的观测值与这n个点是来源于同一分布吗？针对此类问题，Schölkopf et al.（2001）提出了One-Class SVM算法，其思路是：对来源于同一分布的初始观测值，在p维空间中“画出”其“紧边界”（Close Frontier），如果新的点落在“紧边界”的子空间中，就认为新的观测值与初始值来自于同一分布，否则认为新的观测值是异常值。可以看出，这个算法的关键前提是训练集必须是“纯净的”，不能含有异常值，否则计算结果将是有偏的。 当训练集不纯净，或者不能确定训练集是否纯净时，一个常用方法是对训练集中正常值的分布做出合理假设，比如假设正常值服从高斯分布，从这个假设出发，一般可以确定正常值在p维空间中的分布“区域”，离这个“区域”比较远的观测值，即认为是异常值，这就是Elliptic Envelope算法的基本思路（Rousseeuw and Van Driessen, 1999）。具体来说，首先计算每一个观测值的鲁棒协方差，以确定一个“椭圆”区域，并忽略区域以外的点；然后假设“椭圆”区域内部的观测值服从高斯分布，计算区域内部所有点的位置及其鲁棒协方差，据此得到马氏距离并算出“孤立度”标准。Elliptic Envelope只适合正常值为“单峰”分布的情形，对“双峰”或“多峰”分布的拟合效果较差。 针对训练集不纯净的情形，Liu et al.（2008）根据随机森林（Random Forest）的基本思想，提出了Isolation Forest算法。IF算法首先随机选择训练集的一个特征，然后在这个特征的最大值和最小值之间随机选择分叉值，重复这个过程，直至将一个样本分离出来。上述递归分离过程能以“决策树”的形式表示，分离一个样本所需分叉的次数，即为从根节点到末节点的路径长度，对随机森林所有决策树的路径长度进行平均，就能得到正常值的决策函数。对异常值，根据决策函数计算的路径会短于正常值，因此，如果一个样本的路径偏短，那么就认为这个样本是异常值。IF算法适用性好，能够有效处理“双峰”和“多峰”问题。 另一个适用性比较好的异常值识别算法是Local Outlier Factor（Breunig and Sander, 2000）。LOF算法通过计算每一个观测值的“局部异常因子”，来衡量其异常程度。局部异常因子是给定观测值对其近邻值的“局部密度偏差”（Local Density Deviation），局部密度显著低于近邻的样本即为异常值。在计算时，一个观测值的局部异常因子，等于其k最近邻（K-NearestNeighbors）的平均局部密度与它的局部密度的比值：正常值的局部密度与其k最近邻均值接近，而异常值的局部密度会明显低于其k最近邻均值。局部密度是根据观测值之间的距离计算出来的。LOF算法适用性最好，即使异常值来源于不同分布，也能有效进行处理。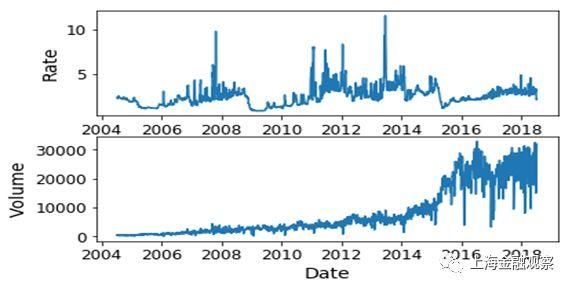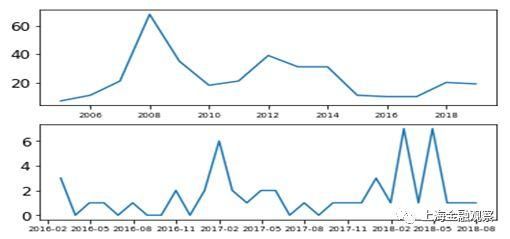 二、算法选择和学习结果 质押式回购是银行间市场的主要交易。这一部分以质押式回购交易为例，使用LOF和IF两种算法，识别市场异常波动及其潜在规律。 （一）数据描述和算法选择 采用银行间市场质押式回购交易的日度数据，时间跨度从2004年7月13日至2018年7月9日，共3499个观测值；每个观测值包含三个维度：时间、加权平均利率和成交额。图1为加权平均利率（Rate）和成交额（Volume）随时间的变化，其中利率单位是百分数，成交额单位是亿元。从图1可以看出，观测期内加权平均利率和成交额均表现出非平稳性，也就是说，数据分布（包括正常值和异常值）随时间发生了变化。因此，我们选择比较“安全”的LOF和IF算法训练机器学习模型。 图1：质押式回购加权平均利率和成交额（日度） （二）学习过程和识别结果 在训练机器学习模型之前，还要把数据集切分成训练集和测试集：算法从训练集中“学习”潜在的决策函数，用于测试集以观察“学习”效果。这里以2004年7月13日至2016年12月31日的观测值为训练集，以2017年1月1日至2018年7月9日的观测值为测试集。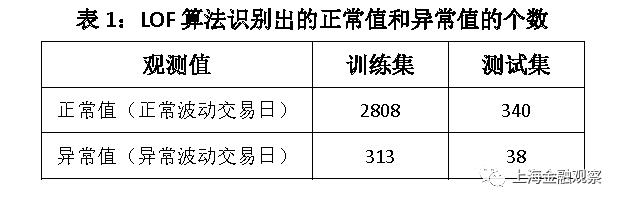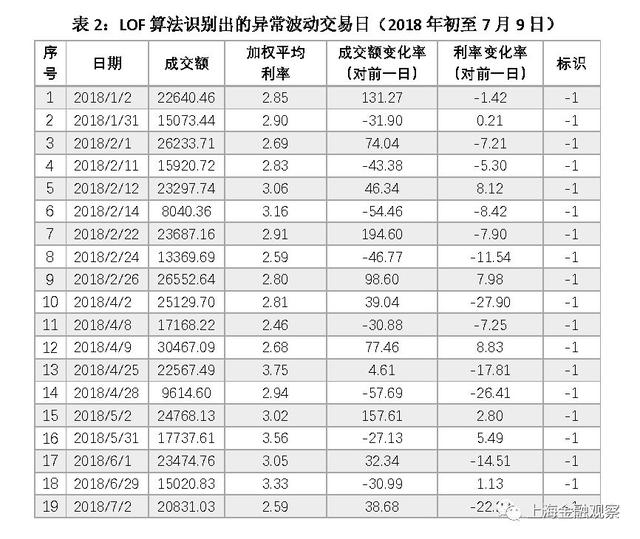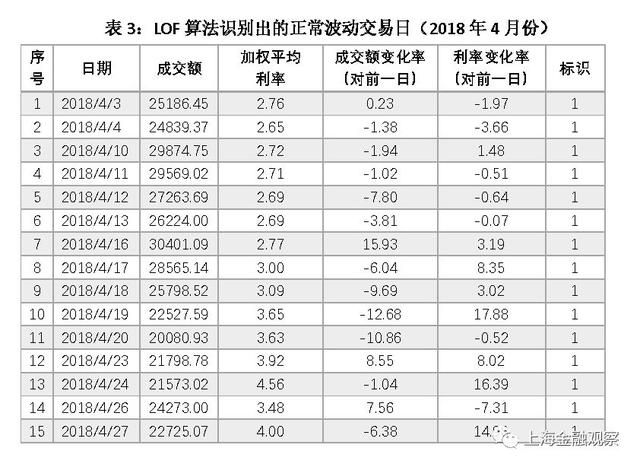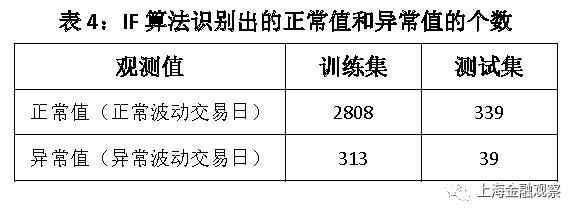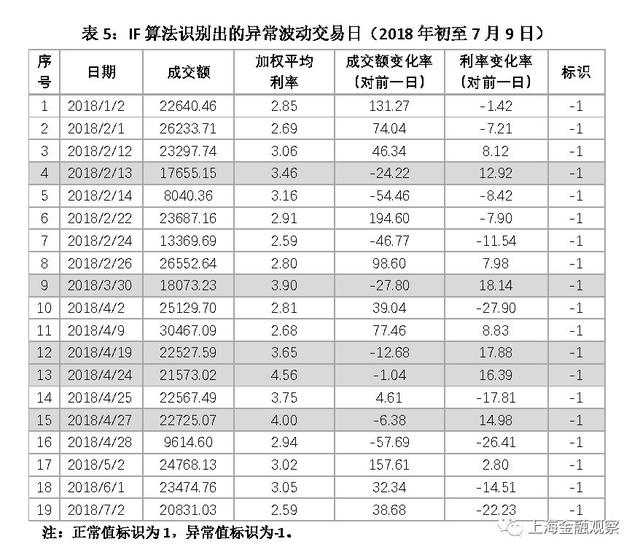 LOF算法的学习结果   LOF算法中需要设定的参数是K最近邻的个数n，一般取默认值n=20，如果异常值比例过高（超过10%），也可以把K最近邻的个数向上调整。我们将K最近邻个数设为默认值，以下为学习结果： 训练集有3121个观测值，即2004年7月13日至2016年12月31日的3121个交易日，LOF算法识别出异常波动交易日313天，占比10.02%。测试集有378个观测值，即2017年1月1日至2018年7月9日的378个交易日，LOF算法识别出异常波动交易日38天（表1），占比10.05%。 现在分析LOF算法自动识别出的异常波动是不是合理。我们把2018年年初至7月9日的19个异常值列出来（表2），其中异常值标识为-1。可以看出，异常交易日要么表现为成交额大幅变化（如1月2日），要么利率大幅变化（如4月25日），要么成交额和利率均大幅变化（如7月2日）。其次，从时间上看，异常交易日表现出明显的季节性，集中在月初月末、假期前后。特别是2月份和4月份的异常值相对集中，2月15日至21日是春节放假，4月5日-7日是清明节放假，4月29日是劳动节放假。这些特点与我们的经验观察相符，LOF算法对异常波动的判断合乎逻辑。此外，我们还发现，异常交易日倾向于连续出现，有一定的趋势性或者说是“惯性”。 结合LOF算法对正常波动的判断，进一步分析其合理性。这里以2018年4月份的15个正常波动交易日为例（表3）。可以发现，LOF算法自动识别出的正常交易日，成交额以及利率的波动幅度普遍较小，与异常波动对比差异比较明显。需要注意的是4月19日，这是一个算法标识为正常波动的交易日，与异常波动的4月25日相比，利率变化幅度相同，而成交额变化幅度更大。这就产生一个疑问：要么对4月19日的判断有误，要么对4月25日的判断有误？其实这是由LOF算法的特点决定的，在下文中可以看到，采用不同的算法学习结果会有差异，如IF算法将4月19日和4月25日均归为异常波动。 根据LOF算法学习结果，还能发现异常值的其它一些运行规律（图2）。第一， 2008年到2016年，异常波动出现的次数呈下降趋势，2011年（36个）、2013年（21个）有所上升，2016年仅录得14个异常值；此后异常波动有所增加，2017年出现19个异常波动交易日，2018年上半年就有19个异常波动交易日。第二，异常值出现的频率与货币政策松紧存在负相关关系，货币政策放松的阶段异常值出现的次数明显下降，比如2009年、2013年、2015年；2017年以来去杠杆、强监管的大背景下，异常波动交易日明显增加，但仍低于2013年之前。第三，异常波动交易日大部分出现在上半年，尤其集中在2月份和4月份。 图2：LOF算法识别出的异常值数量随时间的变化 2. IF算法的学习结果 IF算法需要设定决策树的数量n，以及训练每棵决策树所需的样本数量b。这里设定n=200、b=200，以下为学习结果： IF算法从3121个观测值中识别出异常波动交易日313天，占比10.02%；测试集中378个观测值，IF算法识别出异常波动交易日39天，占比10.32%。就识别出的异常值的个数看，IF算法与LOF算法高度一致。 现在分析IF算法的判断是否合理，并与LOF算法的学习结果进行比较。我们把2018年年初至7月9日的异常值列出来（表5），IF算法识别出19个异常波动交易日，数量与LOF算法相等。异常波动交易日成交额或利率的变化幅度普遍较大，且有明显的季节性和趋势性，这些特点与LOF一致。在IF算法识别出的异常值中，有14个与LOF相同，占大部分；有5个交易日IF算法认为是异常的，而LOF算法认为是正常的，用灰色底纹突出显示。 分析IF算法与LOF算法判断不一致的结果，可以看出两种算法的差异。IF算法随机选取特征以及特征阀值，从根节点到末节点“垂直”递归分类，它对不同维度给予相同权重。而LOF算法通过计算多维空间中的局部密度进行分类，对于方差较大的维度，它赋予更多的权重。本文研究的例子中，成交额变动幅度更大，因此LOF算法更“重视”成交额，而IF算法对成交额和加权平均利率一视同仁。此外，IF算法的学习结果显示，异常值数量随时间的变化趋势，与LOF算法一致（图3）。 图3：IF算法识别出的异常值数量随时间的变化 三、结论 利用无监督机器学习方法，摒除主观标准，让计算机通过“学习”历史数据，获取对数据潜在模式的“认知”，以识别货币市场异常波动，得到的结果相当合理。算法自动识别出的异常波动有以下特点：成交额或利率的变化普遍较大（LOF算法更偏重成交额的变化，IF算法平等对待成交额和利率的变化）；具有明显的季节性和趋势性；与货币环境的松紧存在负相关关系。那么，就本文要研究的问题而言，应该以哪一种算法的结果为准呢？这也可以用机器学习的思路解决，比如借助集成学习（Ensemble Learning）的理念，把LOF和IF分别作为独立的学习模块，组装进一个集成学习器，最终判断以集成学习器的结果为准。 金融领域不断产生着海量数据，机器学习特别适合处理大数据和高维数据，用无监督算法自动识别货币市场异常波动，只是它在金融市场的一个初步应用。我们碰到的金融问题，基本上可以归结为两类：分类和预测。本文研究的就是一个分类问题：把正常波动归为一类，剩下的就是异常波动；而预测出未来的异常波动，更是市场以及监管各方汲汲以求的梦想。目前，机器学习在分类方面的算法相对成熟，应用非常广泛，预测由于更困难提升空间更大，但无疑为我们打开了一个思路。如果将机器学习算法和传统的时间序列分析技术集合起来，很可能大大提高预测准确度。