简介
最近在看一些图相关的问题。实际上关于图相关的研究和问题已经非常多了。在前面的几篇文章里,我也谈到过图的定义、遍历法,扩展树生成和最短路径等问题。 除了这些问题及应用以外,还有一些比较常见的问题,虽然难度不大,不过经常会在一些情况下碰到。不仔细去考虑的话还是比较难解决的。这篇文章里重点要讨论解决的几个问题分别是检测图的连通性、图中间环的检测和二分图的检测。
图的连通性
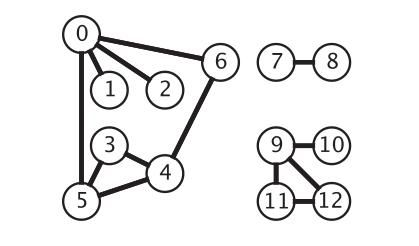
判断一个图的连通性,从概念上来说,就是如果一个图是连通的,那么对于图上面的任意两个节点i, j来说,它们相互之间可以通过某个路径连接到对方。比如下图:
在这个图里,任意的两个节点都可以通过一个路径到达对方。而对于非连通的图来说,它相当于将一个图分割成多个独立的部分,每个部分之间没有任何联系,一个典型的示例如下图:
在这个图里,7,8组成的部分以及9到12所组成的部分它们都是互相隔离的。那么如果要检查和判断一个图是否为连通的,该用什么办法呢?
判断图是否连通
如果仅仅是判断一个图是否为连通的,结合前面讨论图的基础遍历方法,可以有如下的方法。在前面图遍历的方法过程中,我们是从一个指定的点开始,通过不同的策略去遍历这个图,有深度遍历和广度遍历。每次经过一个节点的时候,首先判断一下这个节点是否已经访问过了,如果没有访问过,则这个节点可以作为下一次继续遍历的候选。因为如果这个图是连通的话,这种方法最终会覆盖到整个图。所以可以采用一种计数统计的方式来实现。比如说每次访问一个以前没有遍历的节点,则将对应的计数加一。这样当最后遍历结束后,如果统计的节点和图本身的节点一样的话,表示这个图是连通的,否则表示不连通。在前面的图定义里有相关实现,这里把部分代码给转贴过来。
深度优先遍历:
public class DepthFirstSearch {
private boolean[] marked;
private int count;
private final int s;
public DepthFirstSearch(Graph g, int s) {
marked = new boolean[g.getVertices()];
this.s = s;
dfs(g, s);
}
private void dfs(Graph g, int v) {
marked[v] = true;
count++; //计数,统计访问过的节点
for(int w : g.adj(v))
if(!marked[w]) {
dfs(g, w);
}
}
public boolean marked(int w) {
return hasPathTo(w);
}
public int count() {
return count;
}
}
广度优先遍历:
private void bfs(Graph g, int s) {
Queue queue = new LinkedList();
marked[s] = true;
queue.enqueue(s);
while(q.size() > 0) {
int v = queue.remove();
for(int w : g.adj(v))
if(!marked[w]) {
marked[w] = true;
queue.add(w);
count++; //统计计数
}
}
} 这种方法用来判断整个图是否为连通的时候,实际上只要给定一个点,然后按照给定的步骤可以把改点所连接的所有点都涵盖到。如果有其它分隔的部分则没有再处理了。所以,通过这种办法我们在图不是连通的情况下,它只需要涵盖图的一部分就执行结束了。最坏的情况时间复杂度也就是O(V+E)。
这种办法如果用来单纯判断一个图是否连通确实很有效。但是,在某些情况下,我们需要考虑的不仅仅是判断整个图是否为连通这么简单。比如说,有时候我们需要考虑,给定两个节点i, j,需要判断它们是否相互连接的。这就是我们接着需要考虑的问题。
图中间任意两个点的连通性
因为有时候要考虑的是给定两个点,看它们之间是否连通。所以可能有很多种情况。比如说当整个图是连通的,则它们必然是连通的。而如果整个图不是连通的,但是这两个点是在一个连通的块,它们也是相互连通的。
对于这个问题,该怎么来分析呢?从前面判断图是否连通的过程里,我们可以借鉴到一点思路。首先,对于一个连通的块,按照给定的遍历方法,肯定可以把这一块给覆盖。可是,假设把某一块覆盖了,对于这个被覆盖的区域内的点,随意给定两个,我们怎么知道它们就是连通的呢?这就是这个问题的关键点。在前面的图遍历算法里,当我们每经过一个节点的时候,就将一个boolean数组marked里对应的元素设置为true。那么这里是不是也可以这样来做呢?
比如下图中的0到6节点部分,假设这部分被涵盖之后。他们对应的marked部分为true。可是对于7,8节点呢?它们也要在后面的部分里遍历覆盖,至少保证7和8是连通的,只是它们和外面其他点没有关系。
所以,从前面的讨论里可以看出来。光遍历一个连通的块是不够的,肯定要遍历完所有的块。另外,如果遍历完一个块仅仅用boolean数组来标志的话还是不够的,比如说当我们遍历完0到6这个部分,它们对应的makred被设置为true。而后面又遍历了节点7,8。对于它们该怎么处理呢?如果也标识为true,我们怎么来表示0到6是互通的,但是它们却和节点7,8没关系呢?所以,问题的关键在于对于每个不同的连通区域,要进行不同的标识。
概括起来,前面要处理的问题主要是两个:1. 遍历图中间所有节点。 2. 所有相通的块必须标识为相同。
对于第二个问题从前面的遍历方法我们已经知道,不管是dfs还是bfs,只要给定一个节点遍历完,这一块地方我们一路做同样的标记就可以了,只要它们相通那么标记也肯定是一样的。而对于要遍历所有节点的问题,这个也好办。无非就是遍历一遍所有的节点,对每个节点都调用遍历方法,不过对于已经访问过的节点则直接跳过。所以在实现的细节上,我们可以考虑用一个计数器和一个数组,对于某个块它设定一个值,然后对应的这个值也放到对应数组的索引的位置里。下一次再遇到一个遍历的块时,对这个计数器加一。这样每次遍历的块的计数器值不同。给定任意两个节点,只要判断一下数组里对应的计数器值是否相同就可以了。
按照前面的这些讨论,详细的实现代码如下:
public class CC {
private boolean[] marked;
private int[] id; // 记录每个节点所属的连通块计数
private int count; //用来标记不同连通块
public CC(Graph g) {
marked = new boolean[g.v()];
id = new int[g.v()];
for(int i = 0; i < g.v(); i++) { //遍历所有节点
if(!makred[i]) {
dfs(g, i);
count++
}
}
}
private void dfs(Graph g, int v) {
marked[v] = true;
id[v] = count;
for(int w : g.adj(v))
if(!marked[w])
dfs(g, w);
}
public boolean connected(int v, int w) {
return id[v] == id[w];
}
public int id(int v) {
return id[v];
}
public int count() {
return count;
}
}前面代码实现的细节点在于我们定义了一个int[] id数组,它保存不同节点的统计值。而count这个统计值则表示相通的块里这个值是一样的。
另外,前面这几个方法用的是深度优先遍历的方法。要改用广度优先遍历的方法也很方便。
图中间环的检测
除了前面测试图连通的问题,还有一个常见的问题就是检测图中间是否存在环。这也是一个很有意思的问题,因为在大多数图的结构中确实是存在环的。而对于一个连通的图来说,如果它不存在环,则可以称其为树了。想到这一步,我们才发现,这个环检测的问题在判断一个图形是否为树的问题这边有很重要的应用。关于判断一个结构是否为树的问题这里不赘述,先把这个图中间环检测的问题给处理清楚。
对于一个存在有环的图,一些常用的形式如下图这样:
从这些图的结构里,我们可以看到一个这样的规律。就是从图中间构成环的任意一个节点开始,如果按照某个方向遍历,最终它某个可以访问的点是它前面已经遍历过的。对于一些特殊的情况,比如两个相邻的节点之间的连接,它们不能定义为环,需要被排除。这也是后面具体实现的细节里需要考虑的。
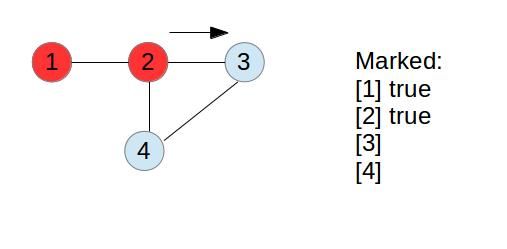
现在结合后面的这个图,我们来进一步细化前面考虑的步骤。假设我们仅仅用原来遍历图的数据结构,我们只是需要有一个boolean[] marked数组就可以了。那么,刚开始的时候,假设从节点1开始去遍历。第一步之后的情况应该如下:
按照前面的标记,makred[1]被标记为true。然后继续考虑1节点所邻接的节点2:
这里有一个问题,就是前面从1遍历到2的时候,设置了marked[2] = true。但是从2为节点再一次进行遍历的时候,可能首先又碰到从2到1的这个关系。这个时候,按照环存在的判断条件,相当于从某个节点出发的时候碰到了一个前面遍历过的节点了。但是2就是从1过来的,如果这种情况判断为真的话则1和2被判断为一个环了。所以需要避免这种情况。要避免这种情况的话,可以增加一个参数,表示访问的当前节点的前一个节点。如果从当前节点所能连接到的节点去遍历的时候,碰到的节点是已经访问过的节点,但是这个节点是它的前一个节点的话,这种情况我们应该忽略。这样,按照前面深度优先遍历的规则,下一步访问的情况如下图:
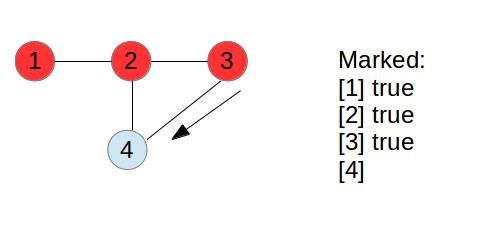
同样,下一步可以访问的节点假设为4,这个时候,对于节点4来说,它的前一个节点是3, 但是它可以遍历到节点2, 而2已经是前面访问过的了,所以这个时候可以判断说确实有环存在。
这是我们考虑到图的一种情况。如果对于图并不是完全连通的情况呢?为了避免遗漏,肯定要尝试去遍历所有的节点,和前面检测图连通性类似。所以,根据前面的讨论,我们后面实现的详细代码如下:
public class Cycle {
private boolean[] marked;
private boolean hasCycle;
public Cycle(Graph g) {
marked = new boolean[g.v()];
for(int i = 0; i < g.v(); i+) {
if(!makred[i])
dfs(g, i, i);
}
}
private void dfs(Graph g, int v, int u) {
marked[v] = true;
for(int w : g.adj(v)) {
if(!marked[w])
dfs(g, w, v);
else if(w != u)
hasCycle = true;
}
}
public boolean hasCycle() {
return hasCycle;
}
}前面实现的代码并不多,重点在于几个地方。一个是前面开始调用dfs方法的时候,传入的节点参数是一个起始节点和它本身作为访问过的前节点。这里是通过一个for循环遍历所有的节点,并通过marked数组来过滤。另外就是dfs方法里,每次取得给定节点v的所有连接点时,我们要判断一下如果这个被访问的节点是前面被访问过而且不是前置节点的话,设置hasCycle为true。表达这个关系的代码是:
if(!marked[w])
dfs(g, w, v);
else if(w != u)
hasCycle = true;这里实现的细节值得仔细去体会。当前,前面遍历的方法是用的深度优先遍历,所以每次当要去遍历下一个节点的时候,只要排除这个节点的前一个节点就可以了。反正深度优先遍历就是这么一个节点一直向前推进到没有了才后退的。所以用一个参数作为前置节点的方式是可行的。我们也可以通过广度优先便利的方式来实现。不过会稍微麻烦点。因为需要记录每个节点的前置节点,需要再额外定义一个数组来表示它们的关系,在后面的判断里结合数组的值来处理。这里只是提出一个这样的思路,具体的实现可以很容易得到。
二分图
还有一个比较重要的问题就是二分图(bipartite)。这个问题有很多的变种,其本质上和着色问题也有很密切的联系。具体的定义就是,假设我们有一个图,对于一个开始的节点,我们尝试用如下的方式去给它着色。总共所有的节点只能着两种色中间的一种。假设为红色或者蓝色。对于一个节点来说,假设它着的是某一种颜色,那么和它相邻的节点只能着和它不同的颜色。那么,给定一个图,如果这个图满足上述的特性的话,则这个图可以称之为二分图。
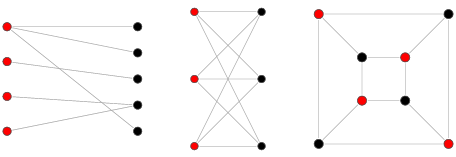
这样的描述显得比较空洞,我们来看一个具体的示例:
图中的这些图形则都可以表示为二分图。因为它们满足给定一个节点,所有和它相邻节点都和它颜色不同的特性。
有了前面几个问题讨论的经验,再来解决它就相对有一点思路了。肯定要判断这个图是否为二分图必然会遍历这个图。然后每次在判断的时候假定一个节点的颜色为某个值,那么再将它相邻的节点颜色都设置成不同的。因为只是两种颜色,可以直接用布尔值类型来处理。另外,对于不属于二分图的情况,肯定是某个节点访问到一个它可以连接到的节点,而这个节点已经被访问过了。但是这个被访问过的节点和当前节点颜色是一样的。这样才能表明它和前面二分图的定义有冲突。所以,我们遍历整个图就是为了过滤提到的这种情况。
那么,在实际实现中可以这样考虑。对于所有节点对应的颜色需要定义一个boolean[] color数组。然后最开始访问一个节点的时候,将其对应color位设置为true,每次访问一个关联的节点时,将关联节点设置成原来节点的相反值。也就是说,比如节点v它的颜色为color[v],那么下一个它被关联的节点的颜色则可以设置成color[w] = !color[v]。正好通过取反实现了颜色的变换。详细实现的代码如下:
public class TwoColor {
private boolean[] marked;
private boolean[] color;
private boolean isTwoColorable = true;
public TwoColor(Graph g) {
marked = new boolean[g.v()];
color = new boolean[g.v()];
for(int i = 0; i < g.v(); i++)
if(!marked[i])
dfs(g, i);
}
private void dfs(Graph g, int v) {
marked[v] = true;
for(int w : g.adj(v)) {
if(!marked[w]) {
color[w] = !color[v];
dfs(g, w);
} else if(color[w] == color[v])
isTwoColorable = false;
}
}
public boolean isBipartite() {
return isTwoColorable;
}
}这里实现的要点还是通过dfs方法,每次碰到一个节点的时候就要判断一下是否已经访问过,已经访问过的话,要判断颜色是否相同。没有的话,则将新节点设置成当前节点的相反值。然后就是要遍历所有节点,防止遗漏未连接的节点情况。代码看起来并不复杂, 细节还是需要慎重考虑。
总结
这是一篇相对来说比较长的博客。之所以写这些主要是图的连通性,图中间环的检测和二分图的检测等问题在很多图应用中都是一个基础。而且因为之前学习这部分的时候遗漏了这几个重要的点,结果导致在一次重要的面试中碰到了这个问题。后来处理的不好,让人非常的悔恨。实际上不管是图的连通性,环也好或者划分也好。它们基本上都是基于一个图遍历的过程和方法。我们常用的图遍历方法比如深度优先和广度优先,它们结合一些其他的数据结构就能够解决这些问题。在解决这些问题的时候,还有一个容易遗漏的地方就是我们很容易忽略图的连通性情况。有的问题只有在图是完全连通的情况下才可以,所以为了避免在图不是全连通情况下的问题,我们必须尽量去遍历所有的节点。
参考材料
Algorithms