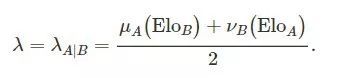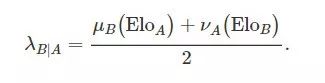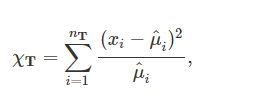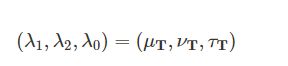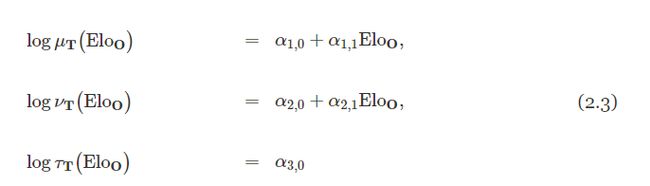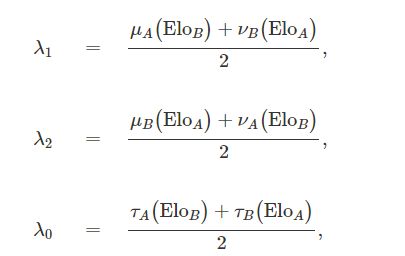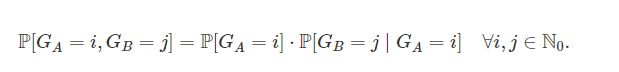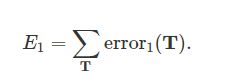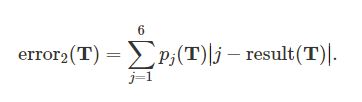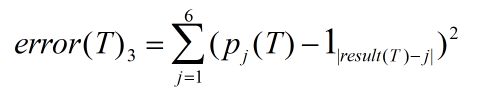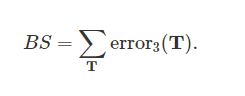大数据文摘出品
编译:halcyon、小鱼
离2018俄罗斯世界杯开幕的日子越来越近,学术界的球迷们也按捺不住期待的心情,纷纷用算法对2018世界杯的比赛结果进行预测。
巧的是,AI的预测结果纷纷看好德国队。前有德国帕绍大学(Universität Passau)利用ELO评级预测德国胜算最大,后有俄罗斯彼尔姆国立研究大学利用神经网络预测世界杯前三名将是德国队、巴西队和阿根廷队,并称这项预测的准确度超过80%。
从AI的预测结果来看,德国队更胜一筹。那么是如何进行预测的呢?一起和文摘菌来看看帕绍大学这篇最近发表的论文。
在大数据文摘后台回复“世界杯”可下载论文~
下面是论文精华内容:
本文提出了一种分析和预测足球锦标赛的方法。该方法基于泊松回归模型,由作为协方差的团队Elo评级和球队特定效应的差异组成。
通过自然中立的拟合从2010年以来所有参加比赛的球队的数据获得预测2018年世界杯的模型。基于单场比赛的估计模型,利用蒙特卡罗模拟计算了2018年世界杯各球队到达不同阶段的概率。
我们提出了两个基于随机序级变量的评分函数,并与排名概率分数对2010~2014年世界杯模型结果进行验证。
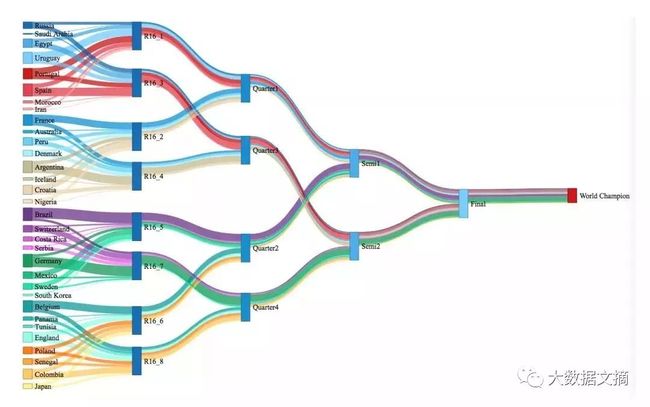
所有模型的预测结果都表示,德国队将成为2018年俄罗斯世界杯的冠军。所有可能的比赛和获胜概率利用桑基图进行了可视化。
我们提出了四个复杂度依次递增的泊松回归模型。模型的验证涉及拟合优度检验、残差分析和最小信息准则(AIC)。此外,我们还对2010~2014年世界杯的模型进行了验证。
首先,利用技巧得分排名概率(RPS)和随机序级变量对每个单场比赛的结果进行了建模,表示为G_A:G_B,其中G_A和G_B分别是球队A和B的进球个数,并利用提出的评分函数在RPS和布莱尔分数上进行了比较。在2010~2014年世界杯的验证上,评分函数与比赛结果非常接近。
模型
我们的模型是基于球队的世界足球ELO评级建立的。该评级来自Elo评级系统,但是为了考虑到各种足球特定变量,我们做了一些修正。2018年3月28号排名最高的5个球队的ELO评级如下:
下面我们展示了四个更加复杂的模型,在这些模型中,(G_A,G_B)为二维泊松分布随机变量,(G_A,G_B)的分布将取决于A球队和B球队以及两个队伍的ELO排名Elo_A和Elo_B。
独立泊松回归模型
在这个模型中我们假设G_A和G_B分别是参数为λ_A|B和λ_B|A的独立泊松分布变量。我们通过A和B的ELO分数进行泊松回归来估计λ_A|B和λ_B|A。具体过程如下:
1.第一步,对球队A与另一支给定Elo分数Elo=Elo_B的球队B的进球数目进行建模,
2.同理,对球队B与另一支给定Elo分数Elo=Elo_A的球队A的进球数目进行建模,
3.我们建模进球数目G_A为具有如下参数的泊松分布:
以此类推,我们有:
对于每个队伍,分别估计他们的回归参数α0,α1,β0和β1。那么A和B之间的比赛就通过两个泊松随机变量G_A和G_B进行模拟。
回归作图
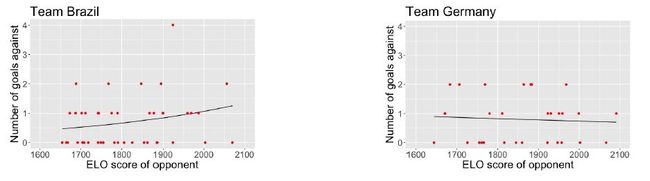
我们利用公式(2.1)做出了德国队和巴西对的回归结果(如下图),其中,红色的点代表观测到的数据(进球数目(y轴)依赖于对手(x轴)的实力)。直线表示依据对手的Elo实力得到的估计均值。
类似的,下图表示公式(2.2)的回归结果:
拟合优度检验
我们对所有参赛队伍的(2.1)和(2.2)中的泊松回归进行拟合优度检验,对于任意一支队伍T,我们计算它的χ^2统计量:
其中,n_T是T的比赛场数,x_i是T在比赛i中的进球数目,μ^_i是估计的泊松回归均值。
我们发现回归模型对大多数队伍的拟合程度较好。下表给出了排名前5的队伍的p值:
偏差分析
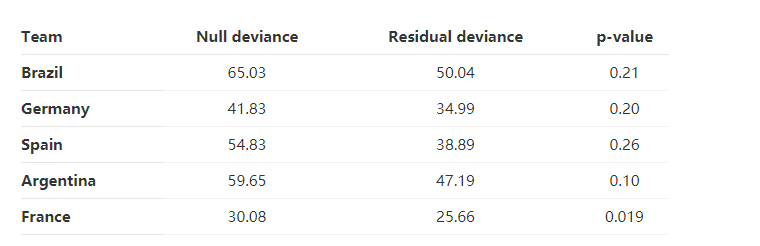
首先,我们计算每个球队在公式(2.1)回归时的空模型偏差和残余偏差。下表显示了偏差值和当前Elo排名前五的团队残余偏差的p值。尽管一些p值非常低,但是还可以接受。
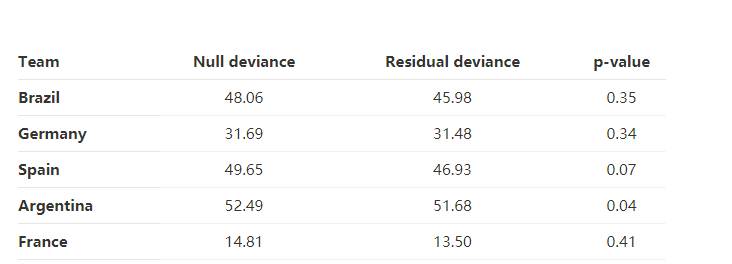
公式(2.2)的回归偏差和p值如下表:
二维泊松回归模型
上一个模型的缺陷在于进球数目G_A和G_B是独立分布。在这一章节中我们提出了一个二维回归模型,模型使用下面的回归方法:
1.对于每支参赛队伍T,我们估计参数
这些参数会依赖于对手队伍O的Elo实力Elo_O,为此,我们使用下面的泊松回归模型:
也就是说,队伍T与Elo实力为Elo_O的对手比赛的估计期望进球数为μ_T(Elo_O)+τ_T,而Elo实力为Elo_O的队伍与T比赛的估计期望进球数量为ν_T(Elo_O)+τ_T。
2.估计λ1、λ2和λ0如下形式:
3.最后,我们假定(G_A,G_B)为具有参数(λ1,λ2,λ0)的二维泊松分布。
具有对角膨胀的二维泊松回归
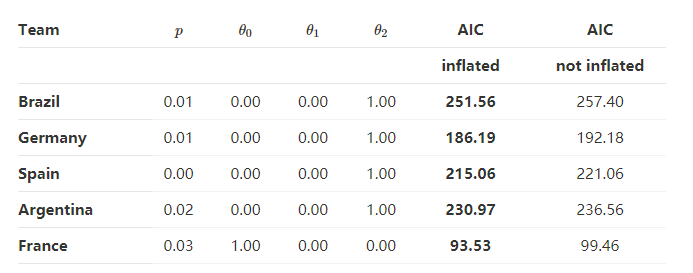
我们以概率p膨胀对角线元素,膨胀通过向量(θ0,θ1,θ2)给定来描述比赛结果0:0,1:1,2:2的概率,我们比较了前5支队伍的对角膨胀模型和非对角膨胀模型的AIC值,如下表所示。从表中可以看出,尽管对角膨胀的ACI值降低了,我们也不认为膨胀模型改善了预测结果。
嵌套的泊松回归模型
该模型的泊松比率λ_A|B和λ_B|A由如下方式确定:
1.我们经常假定相比与B,A具有更高的Elo值,这种假定是有道理的,因为通常强队会主导弱队的战术,进而,强队的进球数目会对弱队的进球数目产生影响。比如,如果A队进了5个球,那么B队可能会进1~2个球,因为A队的防守会因为预期的胜利而注意力不集中,如果强队A进了一个球,那么B队是不可能进球的或者只能进一个球,因为A会更加集中于防守,来守护这来之不易的胜利。
2.G_A的泊松比率由如下公式决定:
3.B队进球数目G_B依赖于Elo值E_A=Elo_A以及G_A的结果,因此G_B建模为具有参数λB(E_A,G_A)的泊松分布:
4.A和B比赛的结果通过首先实现G_A,然后实现G_B进行模拟。
这种方法能够通过条件概率的的定义进行判定:
我们利用历史数据进行了模型验证。
评分函数
下面我们想比较前两届世界杯的预测值和真实值的结果,为了这个目的,我们首先引进了下面的公式,对于队伍T:
下面的评分函数测量和比较预测结果和真实结果:
1.极大似然分数:队伍T的错误定义如下,
总的错误分数由累加所有参赛队伍的错误给出:
2.加权差异:队伍T的错误定义如下,
总的错误分数由累加所有参赛队伍的错误给出:
3.布莱尔分数:队伍T的错误定义如下,
总的错误分数由累加所有参赛队伍的错误给出:
4.RPS:队伍T的错误定义如下,
总的错误分数由累加所有参赛队伍的错误给出:
在2014年世界杯结果上进行模型验证
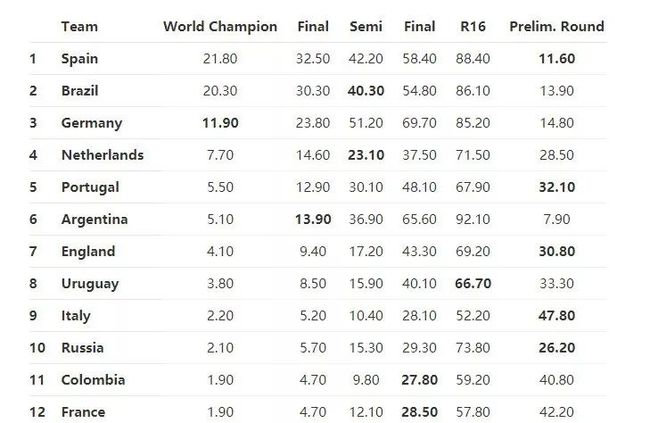
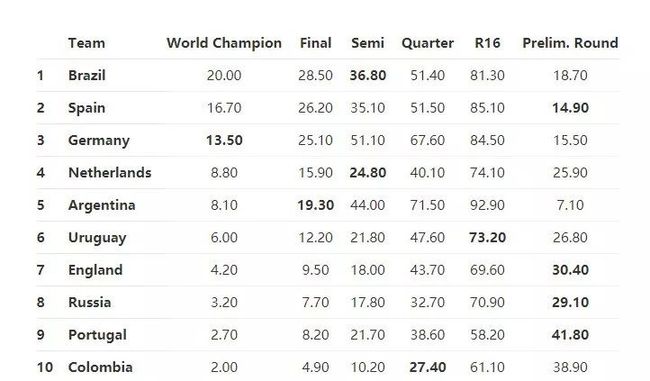
仿真结果如下表格所示,对于每支队伍,我们估计了它到达某一轮或者赢得锦标赛的概率:
这意味着巴西队有20.30%的概率赢得世界杯,30.30%的概率到达决赛,40.30%的概率到达半决赛。最后一列给出了在小组赛离开的概率。独立回归模型和嵌套回归模型的结果如下表所示:
独立回归模型结果
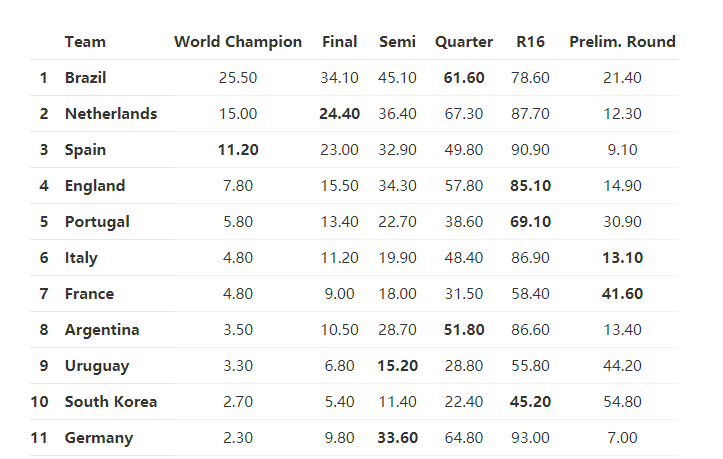
嵌套回归模型结果
在2010年世界杯结果上进行模型验证
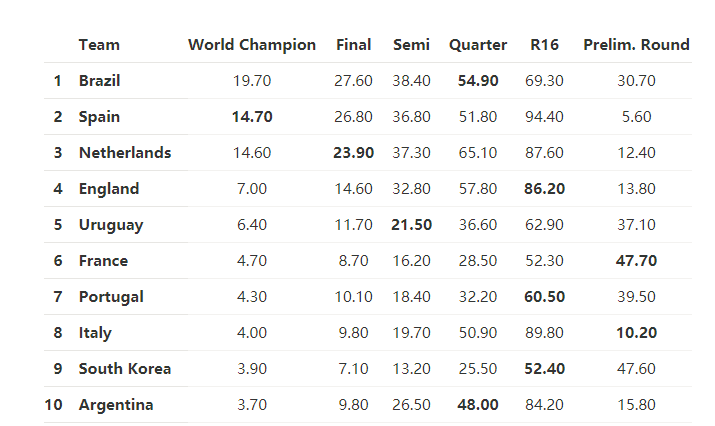
独立回归模型和嵌套回归模型的结果如下:
独立回归模型结果
嵌套回归模型结果
2018年世界杯模型
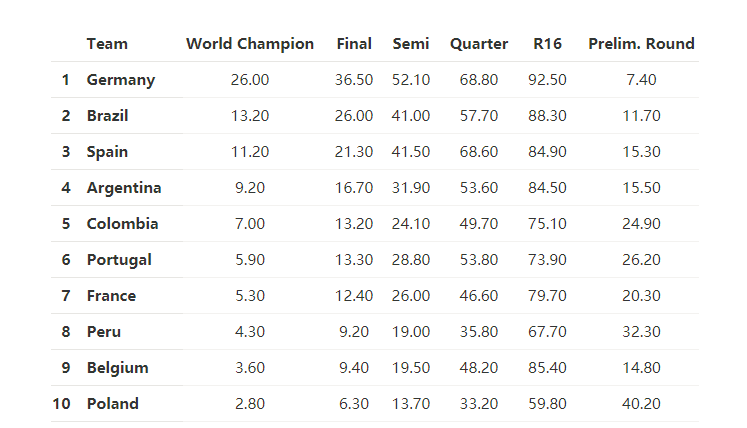
所有模型的预测结果都表示,在考虑球队特点和以下事实的基础上,德国队会赢得冠军:如果德国队和巴西队都赢得了他们的小组赛,他们只会在决赛中相遇。2018年世界杯预测结果:
独立回归模型预测结果
嵌套回归模型预测结果
二维泊松回归模型预测结果
对角膨胀泊松回归模型预测结果
桑基图
我们用桑基图展示了嵌套泊松分布的预测结果,如下图所示。线条的宽度表示了每个球队在不同的赛程胜出的概率。
在大数据文摘后台回复“世界杯”可下载论文~
相关报道:
https://tech.sina.com.cn/roll/2018-06-09/doc-ihcscwxc1117168.shtml?sendweibouid=1642634100