pytorch实现mnist手写数字识别(一)
- 深度学习的神经网络往往是庞大的,有几十层或几百层,这就是“深度”一词的由来。你可以只用权重矩阵来构建一个这样的深层网络,但是一般来说,这是非常麻烦和难以实现的。PyTorch有一个很好的模块
nn,它提供了一种有效构建大型神经网络的好方法。
# Import necessary packages
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import numpy as np
import torch
import helper
import matplotlib.pyplot as plt
- 现在我们要建立一个更大的网络来解决一个(之前的)难题,识别图像中的文本。这里我们将使用MNIST数据集,它由手写灰度数字图像构成。每张图片是28x28像素,您可以看到下面的示例:
- 我们的目标是建立一个神经网络,可以获取这些图像中的一个并预测图像中的数字。
- 首先,我们需要得到我们的数据集。这是通过torchvision包提供的。下面的代码将下载MNIST数据集,然后为我们创建培训和测试数据集。不要太担心这里的细节,你稍后会了解更多。
### Run this cell
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)),
])
# Download and load the training data
trainset = datasets.MNIST('~/.pytorch/MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# print(trainloader)
我们将训练数据加载到trainloader中,并使用iter(trainloader)使其成为迭代器。稍后,我们将使用这个循环数据集进行训练,比如:
for image, label in trainloader:
## do things with images and labels
- 您会注意到我创建了批大小为64的
trainloader,shuffle=True。batch_size是我们在一次迭代中从数据加载器获得图像数量,通常称为批处理。shuffle=True每次我们再次开始遍历数据加载器时,都要对数据集进行shuffle。但这里我只是抓到第一批,这样我们就可以查看数据了。我们可以在下面看到,图像只是一个大小为(64,1,28,28)的张量。因此,每批64个图像,1个彩色通道,28x28个图像。
dataiter = iter(trainloader)
images, labels = dataiter.next()
print(type(images))
print(images.shape)
print(labels.shape)
<class 'torch.Tensor'>
torch.Size([64, 1, 28, 28])
torch.Size([64])
这就是其中一张照片的样子。
plt.imshow(images[1].numpy().squeeze(), cmap='Greys_r');
-
首先,让我们尝试使用权重矩阵和矩阵乘法为这个数据集构建一个简单的网络。然后,我们将看到如何使用PyTorch的
nn模块来实现这一点,该模块为定义网络体系结构提供了一种更加方便和强大的方法。 -
到目前为止,您看到的网络称为全连接网络。一层中的每个单元都连接到下一层中的每个单元。在全连接网络中,每一层的输入必须是一维向量(可以作为一批多个示例叠加成二维张量)。然而,我们的图像是28x28的2d张量,所以我们需要将它们转换成1D向量。考虑到图像的大小,我们需要将一批具有形状(64,1,28,28)的图像转换为具有形状(64,784)的图像,784是28×28。这通常称为展平,我们将二维图像展平为一维向量。
-
这里我们需要10个输出单位,每个数字一个。我们希望我们的网络能够预测图像中显示的数字,所以我们要做的是计算图像属于任何一个数字或类的概率。这最终是类(数字)上的离散概率分布,它告诉我们图像的最可能属于哪一类。这意味着我们需要10个输出单位,用于10个类(数字)。接下来我们将看到如何将网络输出转换为概率分布。
练习:首先,展平一批图像。然后,利用随机张量的权值和偏差,建立一个包含784个输入单元、256个隐藏单元和10个输出单元的多层网络。现在,对隐藏层使用sigmoid激活。不激活输出层,接下来我们将添加一个概率分布。
## Your solution
def activation(x):
return 1/(1+torch.exp(-x))
# Flatten the input image
inputs = images.view(images.shape[0],-1)
# Create parameters
w1 = torch.randn(784,256)
b1 = torch.randn(256)
w2 = torch.randn(256,10)
b2 = torch.randn(10)
h = activation(torch.mm(inputs,w1) + b1)
out = torch.mm(h,w2) + b2
print(out)
tensor([[ 1.4445e+01, -2.4370e+00, -1.5834e+00, 1.1148e+01, -1.3730e+01,
-4.7537e+00, 4.9938e+00, -1.1234e+01, 7.7436e-01, -1.8633e+00],
...,
-5.0983e+00, 2.4600e+00, -7.6534e+00, 8.2278e+00, -8.3573e+00],
[ 1.8891e+01, 4.5289e+00, -7.1427e+00, 2.5687e+01, -7.6912e+00,
-1.0540e+01, -8.1520e+00, -2.1016e+01, 1.4421e+01, 4.0628e+00],
[ 5.5792e+00, -8.7805e+00, -8.6987e+00, 2.0828e+01, -7.1683e+00,
1.7617e+00, -3.0304e+00, -2.2572e+01, -1.8938e+00, -4.7331e+00]])
- 现在我们的网络有10个输出。我们想把一个图像传给我们的网络,得到一个类的概率分布,这个类告诉我们图像可能属于哪个类。像这样的东西:
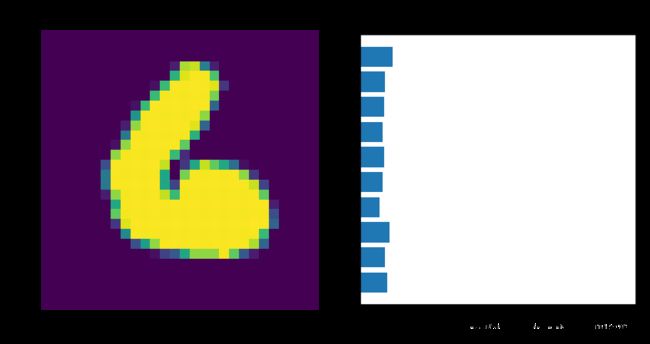
- 在这里,我们看到每个类的概率大致相同。这表示一个未经训练的网络,它还没有看到任何数据,所以它只返回一个均匀分布,每个类的概率相等。
- 为了计算这个概率分布,我们经常使用softmax函数。从数学上看
σ ( x i ) = e x i ∑ k K e x k \Large \sigma(x_i) = \cfrac{e^{x_i}}{\sum_k^K{e^{x_k}}} σ(xi)=∑kKexkexi
- 这样做目的是保证每个输入 x i x_i xi 都在0到1之间,并规范化这些值,以给出一个适当的概率分布,其中概率总和为1。
练习:实现一个函数softmax,它执行softmax计算并返回批中每个示例的概率分布。请注意,执行此操作时需要注意形状。
def softmax(x):
return torch.exp(x)/torch.sum(torch.exp(x),dim=1).view(-1,1)
# Here, out should be the output of the network in the previous excercise with shape (64,10)
probabilities = softmax(out)
# Does it have the right shape? Should be (64, 10)
print(probabilities.shape)
# Does it sum to 1?
print(probabilities.sum(dim=1))
torch.Size([64, 10])
tensor([1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
1.0000])
使用pytorch建立神经网络
PyTorch提供了一个模块 nn,使构建网络变得简单多了。在这里,我将向您展示如何用784个输入、256个隐藏单元、10个输出单元和一个softmax输出来构建与上面相同的一个。
from torch import nn
class Network(nn.Module):
def __init__(self):
super().__init__()
# Inputs to hidden layer linear transformation
self.hidden = nn.Linear(784, 256)
# Output layer, 10 units - one for each digit
self.output = nn.Linear(256, 10)
# Define sigmoid activation and softmax output
self.sigmoid = nn.Sigmoid()
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
# Pass the input tensor through each of our operations
x = self.hidden(x)
x = self.sigmoid(x)
x = self.output(x)
x = self.softmax(x)
return x
让我们慢慢地看。
class Network(nn.Module):
这里我们从 nn.Module继承。结合 super().__ init__() 创建一个跟踪体系结构的类,并提供许多有用的方法和属性。为网络创建类时,必须从nn.Module继承。类本身的名称可以是任何内容。
self.hidden = nn.Linear(784, 256)
这行创建一个用于线性转换的模块 x W + b x\mathbf{W} + b xW+b,有784个输入和256个输出,并将其分配给self.hidden。模块会自动创建weight和bias张量,我们将在forward方法中使用这些张量。使用net.hidden.weight和net.hidden.bias创建网络(net)后,可以访问weight和bias张量。
self.output = nn.Linear(256, 10)
类似地,这将创建另一个具有256个输入和10个输出的线性变换。
self.sigmoid = nn.Sigmoid()
self.softmax = nn.Softmax(dim=1)
这里我定义了sigmoid激活函数和softmax的操作。在nn.Softmax中设置dim=1计算各列的softmax。
def forward(self, x):
使用 nn.Module创建的PyTorch网络必须定义一个forward方法。 它接受张量x并将其传递给您在__init__方法中定义的操作。
x = self.hidden(x)
x = self.sigmoid(x)
x = self.output(x)
x = self.softmax(x)
在这里,输入张量x进行操作,然后重新分配给x。 我们可以看到输入张量通过hidden层,然后是sigmoid函数,然后是output层,最后是softmax函数。 只要在操作中输入和输出与您要构建的网络体系结构相匹配,在此为变量命名都没有关系。 在__init__方法中定义事物的顺序并不重要,但是您需要在forward方法中正确地对操作进行排序。
现在我们可以创建一个网络对象。
# Create the network and look at it's text representation
model = Network()
print(model)
Network(
(hidden): Linear(in_features=784, out_features=256, bias=True)
(output): Linear(in_features=256, out_features=10, bias=True)
(sigmoid): Sigmoid()
(softmax): Softmax(dim=1)
)
您可以使用torch.nn.functional模块更加简洁明了地定义网络。 这是您将看到的网络定义为最常见的方式,因为许多操作都是简单的元素方式函数。 我们通常将此模块定义为import torch.nn.functional as F。
import torch.nn.functional as F
class Network(nn.Module):
def __init__(self):
super().__init__()
# Inputs to hidden layer linear transformation
self.hidden = nn.Linear(784, 256)
# Output layer, 10 units - one for each digit
self.output = nn.Linear(256, 10)
def forward(self, x):
# Hidden layer with sigmoid activation
x = F.sigmoid(self.hidden(x))
# Output layer with softmax activation
x = F.softmax(self.output(x), dim=1)
return x
激活函数
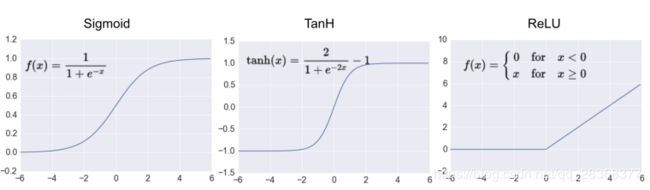
到目前为止,我们只研究了sigmoid激活函数,但是通常任何函数都可以用作激活函数。 唯一的要求是,对于网络来说,近似非线性函数,激活函数必须是非线性的。 以下是一些常见的激活函数示例:Tanh(双曲正切)和ReLU(线性校正单元)。
实际上,ReLU函数几乎专门用作隐藏层的激活函数。
创建多层网络
练习:创建一个具有784个输入单元的网络,一个具有128个单元的隐层和一个ReLU激活,然后一个具有64个单元的隐层和一个ReLU激活函数,最后是一个具有softmax激活的输出层,如上所示。 ReLU激活函数可以利用
nn.ReLU模块或F.relu函数实现。
按图层的网络类型命名是一个不错的方法。例如,“ fc”表示完全连接的图层。 在编写解决方案代码时,请使用fc1,fc2和fc3作为图层名称。
## Solution
class Network(nn.Module):
def __init__(self):
super().__init__()
# Defining the layers, 128, 64, 10 units each
self.fc1 = nn.Linear(784, 128)
self.fc2 = nn.Linear(128, 64)
# Output layer, 10 units - one for each digit
self.fc3 = nn.Linear(64, 10)
def forward(self, x):
''' Forward pass through the network, returns the output logits '''
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x)
x = F.relu(x)
x = self.fc3(x)
x = F.softmax(x, dim=1)
return x
model = Network()
print(model)
Network(
(fc1): Linear(in_features=784, out_features=128, bias=True)
(fc2): Linear(in_features=128, out_features=64, bias=True)
(fc3): Linear(in_features=64, out_features=10, bias=True)
)
初始化权重和偏置项
这里将会自动为您初始化权重,但是可以自定义它们的初始化方式。 权重和偏差是连接到您定义的层的张量。例如,您可以使用model.fc1.weight来获得它们。
print(model.fc1.weight)
print(model.fc1.bias)
Parameter containing:
tensor([[-0.0226, 0.0333, 0.0146, ..., 0.0298, -0.0240, 0.0174],
[-0.0322, 0.0049, -0.0257, ..., 0.0022, -0.0102, -0.0090],
...,
[ 0.0035, 0.0124, 0.0179, ..., -0.0189, 0.0286, 0.0191]],
requires_grad=True)
Parameter containing:
tensor([ 0.0226, 0.0062, 0.0039, -0.0245, -0.0128, 0.0230, 0.0034, -0.0092,
...,
-0.0211, 0.0169, 0.0084, -0.0007, 0.0350, 0.0187, -0.0236, 0.0140],
requires_grad=True)
对于自定义初始化,我们想就地修改这些张量。 这些实际上是 autograd变量,因此我们需要使用model.fc1.weight.data来获取实际的张量。 一旦有了张量,就可以用零(用于偏差)或随机正态分布值填充它们。
# Set biases to all zeros
model.fc1.bias.data.fill_(0)
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
...,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0.])
# sample from random normal with standard dev = 0.01
model.fc1.weight.data.normal_(std=0.01)
tensor([[ 4.5523e-03, 2.8657e-03, -1.5015e-04, ..., -2.1070e-02,
-1.6504e-03, -4.8392e-03],
[-2.0217e-02, 4.0232e-03, 6.3457e-03, ..., 9.6438e-03,
1.2516e-02, -1.1635e-02],
[ 1.1426e-03, 1.5297e-04, -1.6124e-03, ..., -1.3250e-02,
1.5046e-02, 6.9769e-03],
...,
[ 5.4590e-06, -7.0351e-03, 2.4117e-02, ..., 4.7201e-03,
-2.1668e-03, 3.2850e-03],
[ 5.2893e-03, 7.5558e-03, -6.5974e-03, ..., -1.3320e-02,
9.0465e-03, 1.1979e-02],
[-6.0043e-04, 8.7822e-03, 5.4735e-04, ..., 6.5182e-03,
-2.9462e-03, 1.6791e-04]])
前向传播
现在我们有了一个网络,让我们看看传递图像时会发生什么。
# Grab some data
dataiter = iter(trainloader)
images, labels = dataiter.next()
# Resize images into a 1D vector, new shape is (batch size, color channels, image pixels)
images.resize_(64, 1, 784)
# or images.resize_(images.shape[0], 1, 784) to automatically get batch size
# Forward pass through the network
img_idx = 0
ps = model.forward(images[img_idx,:])
img = images[img_idx]
helper.view_classify(img.view(1, 28, 28), ps)
从上面可以发现,我们的网络基本上不知道这个数字是多少。 这是因为我们尚未训练它,所有的权重都是随机的!
使用nn.Sequential
PyTorch提供了一种构建这样的网络的便捷方法,其中张量通过nn.Sequential (documentation)操作顺序传递。 使用它来构建相同效果的网络:
# Hyperparameters for our network
input_size = 784
hidden_sizes = [128, 64]
output_size = 10
# Build a feed-forward network
model = nn.Sequential(nn.Linear(input_size, hidden_sizes[0]),
nn.ReLU(),
nn.Linear(hidden_sizes[0], hidden_sizes[1]),
nn.ReLU(),
nn.Linear(hidden_sizes[1], output_size),
nn.Softmax(dim=1))
print(model)
# Forward pass through the network and display output
images, labels = next(iter(trainloader))
images.resize_(images.shape[0], 1, 784)
ps = model.forward(images[0,:])
helper.view_classify(images[0].view(1, 28, 28), ps)
Sequential(
(0): Linear(in_features=784, out_features=128, bias=True)
(1): ReLU()
(2): Linear(in_features=128, out_features=64, bias=True)
(3): ReLU()
(4): Linear(in_features=64, out_features=10, bias=True)
(5): Softmax(dim=1)
)
在这里,我们的模型与以前相同:784个输入单元,一个具有128个单元的隐藏层,ReLU激活,64个单元的隐藏层,另一个ReLU,然后是具有10个单元的输出层,以及softmax输出。
可以通过传入适当的索引来进行操作。 例如,如果要获得第一个线性运算并查看权重,则可以使用model [0]。
print(model[0])
print(model[0].weight)
Linear(in_features=784, out_features=128, bias=True)
Parameter containing:
tensor([[-0.0047, -0.0203, 0.0070, ..., -0.0073, 0.0203, -0.0019],
[ 0.0242, 0.0299, -0.0162, ..., -0.0110, -0.0216, 0.0247],
[-0.0168, 0.0304, 0.0289, ..., -0.0317, 0.0306, 0.0131],
...,
[-0.0035, -0.0160, -0.0171, ..., -0.0045, -0.0104, 0.0091],
[-0.0018, 0.0039, 0.0196, ..., 0.0281, -0.0169, -0.0170],
[-0.0069, -0.0119, -0.0130, ..., 0.0082, 0.0078, -0.0179]],
requires_grad=True)
您也可以传入OrderedDict来命名各个图层和操作,而不是使用整数访问。 请注意,字典键必须唯一,因此每个操作必须具有不同的名称。
from collections import OrderedDict
model = nn.Sequential(OrderedDict([
('fc1', nn.Linear(input_size, hidden_sizes[0])),
('relu1', nn.ReLU()),
('fc2', nn.Linear(hidden_sizes[0], hidden_sizes[1])),
('relu2', nn.ReLU()),
('output', nn.Linear(hidden_sizes[1], output_size)),
('softmax', nn.Softmax(dim=1))]))
model
Sequential(
(fc1): Linear(in_features=784, out_features=128, bias=True)
(relu1): ReLU()
(fc2): Linear(in_features=128, out_features=64, bias=True)
(relu2): ReLU()
(output): Linear(in_features=64, out_features=10, bias=True)
(softmax): Softmax(dim=1)
)
现在您可以按整数或名称访问图层
print(model[0])
print(model.fc1)
Linear(in_features=784, out_features=128, bias=True)
Linear(in_features=784, out_features=128, bias=True)
在下一次内容中,我们将看到如何训练神经网络来准确预测MNIST图像中出现的数字。