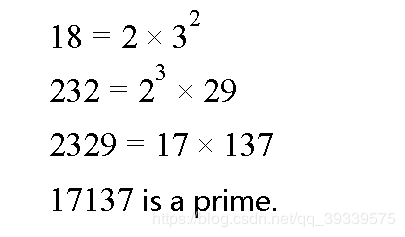浙江大学计算机与软件学院2019年考研复试上机模拟练习

7-1 Conway’s Conjecture

John Horton Conway, a British mathematician active in recreational mathematics, proposed a conjecture in 2014: arrange the factors of any given number in ascending order, and pull the exponents down, we can get another number. Keep doing so we must end up at a prime number.

For example:

Now you are supposed to write a program to make one step verification of this conjecture. That is, for any given positive integer N, you must factorize it, and then test if the number obtained from its factors is a prime.

Output Specification:

For each case, first print in a line the number obtained from N’s factors. The in the next line, print Yes if the above number is a prime, or No if not.

Sample Input 1:

2329

Sample Output 1:

17137
Yes

Sample Input 2:

124

Sample Output 2:

2231
No

Sample Input 3:

87516

Sample Output 3:

2232111317
No

note

1. 要求输出因式阶数的组合形式，一开始读题有点懵，慢慢想边好，从2开始如果能除尽则除到不能再除，
2. 有一个点运行时错误， 原因是分解都是从2开始的，单1的情况没有考虑进去。

Code

#include
using namespace std;
bool isprime(long long  n){
	if(n <= 1) return 0;
	for(long long  i =2 ; i <= sqrt(1.0 * n); i++){
		if(n % i == 0) return 0;
	}
	return 1;
}
string s;
int  main(){

	long long  num,temp,  cnt = 0;
	
	cin >> num;
	temp = num;
	for(long long  i = 2; i < num; i++){
		long long  cnt = 0;
		while(temp % i ==0){
			cnt++;
			temp /= i;
		}
		if(cnt >= 1){
			if(cnt > 1)
				s = s + to_string(i) + to_string(cnt);
			else 
				s = s + to_string(i);
		}

	}
	cout << s << endl;
	if(isprime(stoll(s))) 
		cout << "Yes";
	else 
		cout << "No";

	return 0;
}

7-2 Play with Linked List (25 分)

Input Specification:

Each input file contains one test case. For each case, the first line contains the address of the first node, a positive N (≤10​5​​ ) which is the total number of nodes, and an integer 1≤k

Then N lines follow, each describes a node in the format:

Address Data Next
where Address is the position of the node, Data is a positive integer no more than 105​​ , and Next is the position of the next node. It is guaranteed that there are at least two nodes on the list.

Output Specification:

For each case, output in order the resulting linked list. Each node occupies a line, and is printed in the same format as in the input.

Sample Input:

00100 6 4
00000 4 99999
00100 1 12309
68237 6 -1
33218 3 00000
99999 5 68237
12309 2 33218

Sample Output:

00000 4 68237
68237 6 33218
33218 3 99999
99999 5 12309
12309 2 00100
00100 1 -1

Note

1. 链表的重排序，发现只记录address和data貌似挺普世的，再重试一下其他几道题
2. 注意链表重排序的典型坑： 有节点不参与其中

Code

#include
using namespace std;
const int maxn = 1e7 + 10;
struct node{	
	int data;
	int next;
	int adress;
}a[maxn], b[maxn];
int visited[maxn] = {0};

int main(){
#ifdef _DEBUG
	ifstream cin("data2.txt");
#endif
	int start, num, k, i, j, tempa, tempb, tempc, last;
	cin >> start >> num >> k;
	for(i = 0; i < num; i++){
		cin >> tempa >> tempb >> tempc;
		b[tempa].data = tempb;
		b[tempa].next = tempc;
		b[tempa].adress = tempa;
        visited[tempa] = 1;
	}
	int temp = start;
	for(i = 0; i  < num; i++){
		a[i].data = b[temp].data;
		a[i].adress = b[temp].adress;
		temp = b[temp].next;
        if(visited[temp] == 0 && i != num -1) { num = i + 1; break;}
	}
    fill(visited, visited + maxn, 0);
	int id1 = k - 1, id2 = num - 1, ptr;
	for(i = 0; i < num; ){
		if(i % 2 == 0 && id1 >= 0) ptr = id1--;
		else if(id2 >= 0) ptr = id2--;

		if(visited[ptr] == 0 && i != num - 1){
			visited[ptr] = 1;
			if(i == 0)printf("%05d %d", a[ptr].adress, a[ptr].data);
			else{
				printf(" %05d\n", a[ptr].adress);
				printf("%05d %d", a[ptr].adress, a[ptr].data);
			}
			i++;
		}else if(i == num - 1 && visited[ptr] == 0){
			i++;
			printf(" %05d\n", a[ptr].adress);
			printf("%05d %d -1", a[ptr].adress, a[ptr].data);
		}

	}




#ifdef _DEBUG
	cin.close();
#endif
	return 0;
}

7-3 Unsuccessful Searches

The above figure is a question from GRE-CS 2018. It states:

Given an initially empty hash table HT of size 11. The hash function is H(key)=key%7, with linear probing used to resolve the collisions. Now hash the keys 87, 40, 30, 6, 11, 22, 98 and 20 one by one into HT. What is the average search time for unsuccessful searches?

The answer is 6.

Now you are supposed to write a program to solve this kind of problems.

Input Specification:

Each input file contains one test case. For each case, the first line gives 3 positive integers TSize (≤10​3​​ , the table size), M (≤TSize, the divisor in the hash function), and N (≤TSize, the number of integers to be inserted). Then N non-negative integers (≤10​4) are given in the next line, separated by spaces.

Output Specification:

Print in a line the average search time for unsuccessful searches, after hashing the N integers into the table. The answer must be accurate up to 1 decimal place.

Sample Input 1:

11 7 8
87 40 30 6 11 22 98 20

Sample Output 1:

6.0

Sample Input 2:

3 3 3
81 2 5

Sample Output 2:

4.0

Note

1. 查找hash的失败平均查找长度，第一次读题懵逼，则么有凑不出样例的结构，最后才知道，失败查找长度是指所查元素不在表中，通过(H(temp) + i) % tablesize 找到空项或者找回自己结束所查找的次数之和
2. 低级错误如图， j > 0 忘记了

Code1

#include
using namespace std;
const int maxn = 1010;
int a[maxn] = {0};
int main(){

	int tablesize, num, div, i, negcnt = 0, neglen = 0, temp;
	cin >>tablesize >> div >> num;
  //  if(tablesize <= 1 || div <= 1 || num <= 1) while(1);
    fill(a, a + maxn , -1);
	for(i = 0; i > temp;
		for(int j = 0; j < num; j++){
			int key = (temp  % div + j) % tablesize;
			if(a[key] == -1){ 
				a[key] = temp;
				break;
			}
		}
	}
    int cnt = 0;
    for(i = 0; i < div; i++){
		for(int j = 0;j <= tablesize  ; j++){
			int key = (i % div + j) % tablesize;
			if(a[key] != -1 ){ 
				cnt++;
			}
            if(i == key && j > 0 ) break;
			if(a[key] == -1) {
				cnt++; 
				break;
			}
		}
	}
	printf("%.1lf", 1.0*cnt/div);

	return 0;
}

7-4 Ambulance Dispatch