「hdu6646」A + B = C【哈希】
A + B = C
Problem Description
Hi everyone! Welcome to the Stage 7 7 7 of this series of training contests. Cuber QQ is the problem settler of this contest; he has prepared 11 11 11 problems for you and wishes you to enjoy it. Good luck!
As the first problem of this contest, Cuber QQ thought that it’s reasonable to start with an easy one, so he modified the famous A + B A + B A+B problem by a little bit, so that it’s easy enough but not that trivial.
Given a , b , c a,b,c a,b,c , find an arbitrary set of x , y , z x,y,z x,y,z such that a × 1 0 x + b × 1 0 y = c × 1 0 z a\times 10^x+b\times 10^y=c\times 10^z a×10x+b×10y=c×10z and 0 ≤ x , y , z ≤ 1 0 6 0\leq x,y,z\leq 10^6 0≤x,y,z≤106.
Input
The input consists of multiple test cases, starting with an integer t ( 1 ≤ t ≤ 100 ) t (1\leq t\leq 100) t(1≤t≤100), denoting the number of test cases.
For each test case, there are three space-separated integers, a , b , c a,b,c a,b,c respectively ( 1 ≤ a , b , c ≤ 1 0 100000 ) (1\leq a,b,c\leq 10^{100000}) (1≤a,b,c≤10100000).
Output
For each test case, please output three space-separated integers x , y , z x,y,z x,y,z. If there are multiple solutions, print any of them.
In case there are no solutions, please output − 1 −1 −1 as a single line.
Sample Input
3
23 39 62
2 31 51
1 1 1
Sample Output
0 0 0
1 0 0
-1
Hint
HDOJ may give ambiguous feedback due to the compatibility issue of our checker. If you see “System Error”, please think of it as “Wrong Answer”.
Source
2019 Multi-University Training Contest 7
题意
- 就是给你三个长度为 1 0 5 10^5 105的数 a , b , c a,b,c a,b,c,让你求三个数 x , y , z x,y,z x,y,z,且 0 ≤ x , y , z ≤ 1 0 6 0\leq x,y,z \leq 10^6 0≤x,y,z≤106,使得 a × 1 0 x + b × 1 0 y = c × 1 0 z a\times 10^x+b\times 10^y=c\times 10^z a×10x+b×10y=c×10z
题解
- 首先根据常识可知,两个数 a , b a,b a,b相加等于另外一个数 c c c,记三个数长度分别为 l e n a , l e n b , l e n c len_a,len_b,len_c lena,lenb,lenc那么 l e n c len_c lenc的长度要么是 m a x ( l e n a , l e n b ) max(len_a,len_b) max(lena,lenb),要么是 m a x ( l e n a , l e n b ) + 1 max(len_a,len_b)+1 max(lena,lenb)+1,所以考虑将 a a a或者 b b b高位与c高位或c第二高位处对其,然后去 c h e c k check check a + b a+b a+b可不可能等于 c c c【因为枚举a对齐的时候b也可能需要左移使等式成立】所以就是枚举四种情况去 c h e c k check check就行了
- 然后 c c c最开始需要处理一下,使得他最够长,然后才能 c − a c-a c−a是个正数,所以很容易想到使得c的长度变为 m a x ( l e n c , m a x ( l e n a , l e n b ) + 1 ) max(len_c,max(len_a,len_b)+1) max(lenc,max(lena,lenb)+1),但是注意c的初始值也有可能是这种情况: a + b a+b a+b的值后面有很多 0 0 0,去掉这些 0 0 0得到 c c c,比如说 a = 1111 , b = 100 , c = 1112 a=1111,b=100,c=1112 a=1111,b=100,c=1112这种情况下你不能仅仅在 c c c后面加一个 0 0 0,你需要加两个 0 0 0,换句话说,假设 a , b a,b a,b的后缀 0 0 0的数量分别为 z e r o a , z e r o b zero_a,zero_b zeroa,zerob, c c c的长度应该初始化为 m a x ( l e n c , m a x ( l e n a − z e r o a , l e n b − z e r o b ) + m a x ( z e r o a , z e r o b ) + 1 ) max(len_c,max(len_a-zero_a,len_b-zero_b)+max(zero_a,zero_b)+1) max(lenc,max(lena−zeroa,lenb−zerob)+max(zeroa,zerob)+1),如图所示。
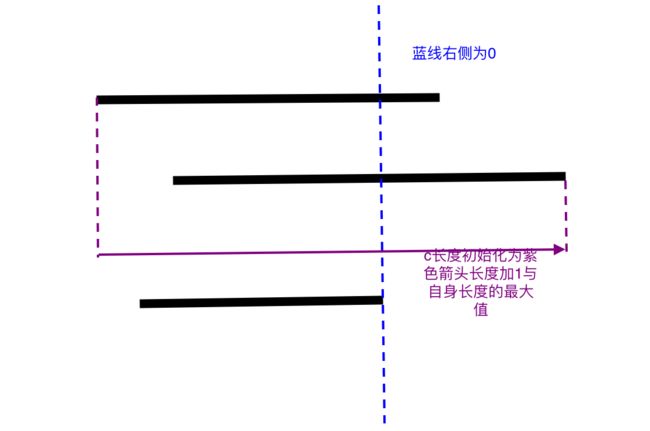
- 然后检查 a + b a+b a+b是否等于 c c c可以使用哈希,就不需要用高精模拟啦,由于这题好像有点卡常,所以没用三哈希,用的双哈希,也有可能是我的哈希不够优秀
代码
#pragma GCC optimize(3)
#include