HDU-6356 Glad You Came多校第五场

给你一个函数，生成一个长度为3*m的数组F，初始化数组A（长度n）全为0，有m次更新操作，每次操作给你一个

区间【l，r】和一个数v对于区间内的数a【i】=max（a【i】，v）。最后求 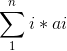   异或和。

用线段树维护区间最大值和最小值，如果最大值小于v那就相当区间更新，如果最小值大于等于v那么就直接忽略。

最后做一次询问，求出全部的a【i】。一个语句决定你T还是A。

#include
using namespace std;
typedef long long LL;
typedef unsigned int UI;
const int maxn = 1e5 + 5;
const int maxm = 5e6 + 5;
const UI mod = (1 << 30);
const int INF = 1e9 + 7;

int n,m;
UI x,y,z,f[maxm*3];
UI a[maxn<<2],b[maxn<<2],lazy[maxn<<2];
UI ans[maxn];
void build(int rt,int nowa,int nowb)
{
    a[rt]=b[rt]=0; lazy[rt]=0;
    if( nowa==nowb ) return;
    int mid=nowa+nowb>>1;
    build(rt<<1,nowa,mid);
    build(rt<<1|1,mid+1,nowb);
}

void down(int rt)
{
    if( lazy[rt]!=0 )
    {
        a[rt<<1]=a[rt<<1|1]=lazy[rt];
        b[rt<<1]=b[rt<<1|1]=lazy[rt];
        lazy[rt<<1]=lazy[rt<<1|1]=lazy[rt];
        lazy[rt]=0;
    }
}
void up(int rt)
{
    a[rt]=max(a[rt<<1],a[rt<<1|1]);
    b[rt]=min(b[rt<<1],b[rt<<1|1]);
}

void updata(int rt,int l,int r,int nowa,int nowb,UI v)
{
    if( b[rt]>=v ) return;  // 这句话不写直接T，懵逼。。。
    if( r=v )
            return;
    }
    down(rt);
    int mid=nowa+nowb>>1;
    updata(rt<<1,l,r,nowa,mid,v);
    updata(rt<<1|1,l,r,mid+1,nowb,v);
    up(rt);
}

void query(int rt,int nowa,int nowb)
{
    if( a[rt]==b[rt] )
    {
        for(int i=nowa;i<=nowb;i++)
            ans[i]=a[rt];
        return;
    }
    down(rt);
    int mid=nowa+nowb>>1;
    query(rt<<1,nowa,mid);
    query(rt<<1|1,mid+1,nowb);
   // up(rt);
}

UI RNG61()
{
    x = x ^ (x << 11);
    x = x ^ (x >> 4);
    x = x ^ (x << 5);
    x = x ^ (x >> 14);
    LL w = x ^ (y ^ z);
    x = y;
    y = z;
    z = w;
    return z;
}

int main() {
    //#ifndef ONLINE_JUDGE
    //freopen("input.txt","r",stdin);
    //#endif
    int t; scanf("%d", &t);
    while(t--)
    {
        scanf("%d%d%u%u%u", &n, &m, &x, &y, &z);
        for(int i = 1; i <= 3 * m; i++)
            f[i] = RNG61();
        UI v,l,r;
        //int ;
        build(1,1,n);
        for(int i = 1; i <= m; i++)
        {
            l = min(f[3*i-2] % n, f[3*i-1] % n) + 1;
            r = max(f[3*i-2] % n, f[3*i-1] % n) + 1;
            v = f[3*i] % mod;
            if( v==0 ) continue;
            updata(1,l,r,1,n,v);
        }
        LL res = 0;
        query(1,1,n);
        for(int i = 1; i <= n; i++)
            res = res^(i*(LL)ans[i]);
        printf( "%lld\n", res );
    }
    return 0;
}