模拟幅度调制相干解调系统抗噪声性能仿真分析
1.引言
由模拟信源产生的携带信息的消息经传感器转换成电信号m(t),譬如,通过话筒将声音转换成电信号,该信号即为模拟信号,在时间和幅度上连续。然而,这样的信号在实际传输中,并不适用,因为其本身所存在低频传输特性差,信噪比较低的问题。要将信号在信道中传输,我们需要对其进行调制到合适的频段。在本文中,我们将对几种典型幅度调制解调系统进行分析,并利用matlab进行仿真验证,在一定的误差范围内,佐证分析。
2.系统模型
2.1 常规调幅
常规调幅(AM)信号的时域表达式为 s A M ( t ) = A c [ 1 + m ( t ) ] c o s ( 2 π f c t ) (1) s_{AM}(t) = A_c[1+m(t)]cos(2{\pi}f_ct) \tag{1} sAM(t)=Ac[1+m(t)]cos(2πfct)(1) 其中,m(t)为基带消息信号, A c c o s ( 2 π f c t ) A_ccos(2{\pi}f_ct) Accos(2πfct)为载波。
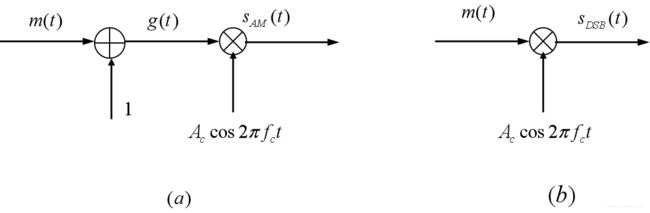
AM信号的产生方案如图1(a)所示
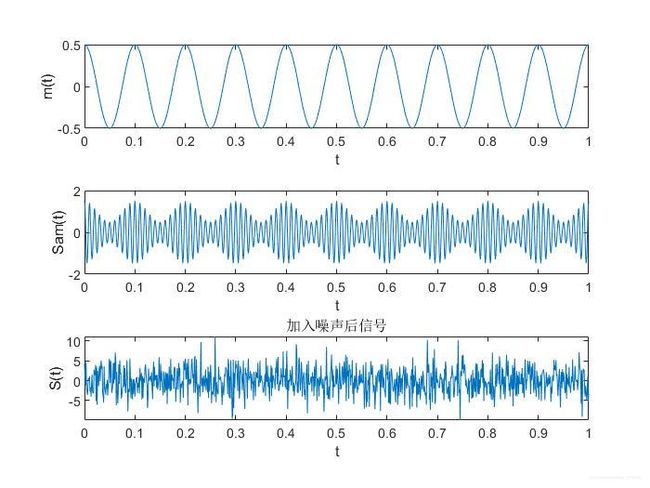
常规调幅信号的波形图如图 2,3 所示.
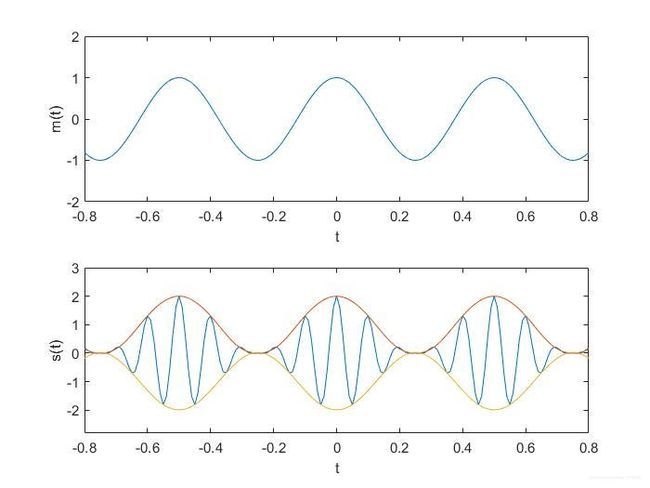
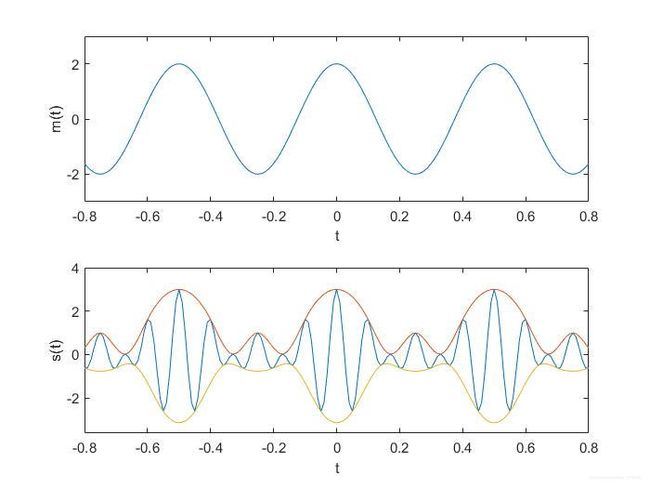
第一幅图为 s A M ( t ) s_{AM}(t) sAM(t)的波形,第二幅图为原信号 m ( t ) m(t) m(t)的图像
在图2和图3 中,给出 ∣ m ( t ) ∣ ≤ 1 \left | m(t) \right| \leq 1 ∣m(t)∣≤1和 ∣ m ( t ) ∣ ≥ 1 \left | m(t) \right| \geq 1 ∣m(t)∣≥1的图像,由图2可见, ∣ m ( t ) ∣ ≤ 1 \left | m(t) \right| \leq 1 ∣m(t)∣≤1时,信号的包络图与 m ( t ) m(t) m(t)相同,故在实际运用中,可以采取包络解调法进行解调。若 ∣ m ( t ) ≥ 1 ∣ \left | m(t)\ge 1 \right| ∣m(t)≥1∣,由图3 可以看到,其包络图中,无法观测到 m ( t ) m(t) m(t)的变化规律。
为计算效率。我们定义传递信号总功率中用于信息部分的功率所占的比例为调制效率。下面计算常规调幅的调制效率。
η A M = P m P A M = P m P m + P c = m ( t ) 2 ‾ 1 + m ( t ) 2 ‾ (2) \eta_{AM} = \frac{P_m}{P_{AM}}=\frac{P_m}{P_m+P_c}=\frac{\overline {m(t)^2}}{1+ \overline{m(t)^2}} \tag{2} ηAM=PAMPm=Pm+PcPm=1+m(t)2m(t)2(2)
为了不产生过调制现象,要满足 ∣ m ( t ) ∣ ≤ 1 \left | m(t) \right| \leq 1 ∣m(t)∣≤1,即 m ( t ) 2 ‾ ≤ 1 \overline{m(t)^2 }\leq 1 m(t)2≤1,可以得到 η A M ≤ 0.5 \eta_{AM}\leq 0.5 ηAM≤0.5,可见常规双边带调制为低效率调制,不利于通信。
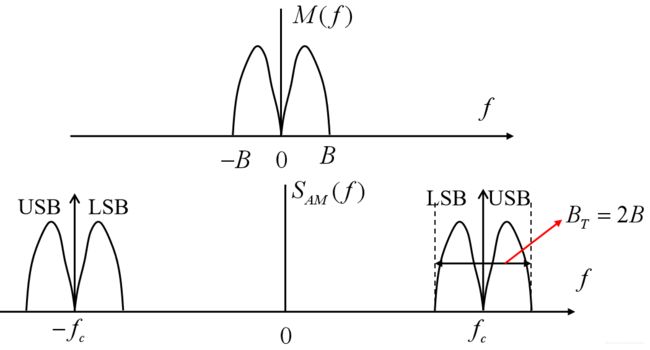
假定调制信号 m ( t ) m(t) m(t)的频谱为 M ( f ) M(f) M(f),由式(1)进行傅里叶变换可以得到AM信号的频谱为 S A M ( f ) = A c 2 [ δ ( f − f c ) + M ( f − f c ) ] + A c 2 [ δ ( f + f c ) + M ( f + f c ) ] (3) S_{AM}(f)=\frac{A_c}{2}[\delta(f-f_c)+M(f-f_c)]+\frac{A_c}{2}[\delta(f+f_c)+M(f+f_c)] \tag{3} SAM(f)=2Ac[δ(f−fc)+M(f−fc)]+2Ac[δ(f+fc)+M(f+fc)](3)
m ( t ) m(t) m(t)与AM信号的频谱如图4所示
2.2 抑制载波双边带调幅
由于常规双边带调制效率较低,为提高调制效率,便产生了一种“没有载波”的调幅方式,成为抑制载波双边带调幅(DSB-SC)。
DSB-SC信号的时域表达式为
s D S B ( t ) = A c m ( t ) ∗ c o s ( 2 π f c t ) (4) s_{DSB}(t) = A_cm(t)*cos(2{\pi}f_ct) \tag{4} sDSB(t)=Acm(t)∗cos(2πfct)(4)
该信号由乘法器产生。如图1(b)所示
根据式(4)进行傅里叶变换,我们可以得到DSB-SC信号的频谱
S D S B ( f ) = A c 2 [ M ( f + f c ) + M ( f − f c ) ] (5) S_{DSB}(f) = \frac{A_c}{2}[M(f+f_c)+M(f-f_c)] \tag{5} SDSB(f)=2Ac[M(f+fc)+M(f−fc)](5)
频域图像如下所示:
DSB-SC信号的功率和调制效率为
P D S B = s D S B 2 ( t ) ‾ = A c 2 m ( t ) 2 c o s 2 ( 2 π ∗ f c ∗ t ) ‾ = A c 2 2 m ( t ) 2 ‾ (6) P_{DSB} = \overline{s_{DSB}^2(t)}=\overline{A_c^2m(t)^2cos^2(2\pi*f_c*t)}=\frac{A_c^2}{2}\overline{m(t)^2} \tag{6} PDSB=sDSB2(t)=Ac2m(t)2cos2(2π∗fc∗t)=2Ac2m(t)2(6)
S A M ( f ) = P m P A M = P m P m + P c = 1 (7) S_{AM}(f)=\frac{P_m}{P_{AM}} = \frac{P_m}{P_m+P_c} = 1 \tag{7} SAM(f)=PAMPm=Pm+PcPm=1(7)
其中, P m P_m Pm为调制前携带信息的信号功率, P A M P_{AM} PAM为调制后的信号总功率。可以看到,由于在调制过程中没有加载波,调制过程变得简单,调制效率也有了明显的提升。但是,从调制后信号的包络图来看,其并不包含原信号的变化规律,因此,并不能使用包络法进行解调。由式(5)和频谱图可以看到,调制后频谱进行了搬移和幅度上的变化,为了恢复原信号,我们需要进行再次搬移以进行解调(解调模型如下所示),在搬移时,要尽可能使用与原载波一模一样的信号进行解调,这使解调过程变得复杂,可见一失一得。
2.3 单边带调制
由上图我们可以看到,常规AM信号和DSB-SC信号在正负频率均有边带,而且是对称的,由对称这一点我们可以得到,如果只有一个边带,也是可以恢复信号的,由此,可以引出另外一种调制,即单边带调制。
单边带调制的公式为
s S S B ( t ) = A c m ( t ) c o s ( 2 π ∗ f c t ) ∗ h S S B ( t ) (8) s_{SSB}(t) = A_cm(t)cos(2\pi*fct) *h_{SSB}(t)\tag{8} sSSB(t)=Acm(t)cos(2π∗fct)∗hSSB(t)(8)
其中, h S S B ( t ) h_{SSB}(t) hSSB(t)为上/下边带滤波器,进行傅里叶变换,可以得到:
S S S B ( f ) = A c 2 [ M ( f − f c ) + M ( f + f c ) ] H S S B ( f ) (9) S_{SSB}(f) =\frac{A_c}{2}[M(f-f_c)+M(f+f_c)]H_{SSB}(f) \tag{9} SSSB(f)=2Ac[M(f−fc)+M(f+fc)]HSSB(f)(9)
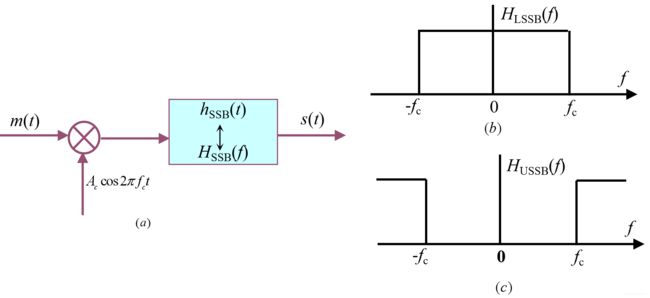
上图中,a为信号产生模型,b,c为 h S S B ( t ) h_{SSB}(t) hSSB(t)为下/上边带滤波器时的频谱。
解调过程与DSB-SC相似,均只能用相干解调。
下图为信号产生的一种方案—滤波法的频域原理

3.抗干扰性能理论分析

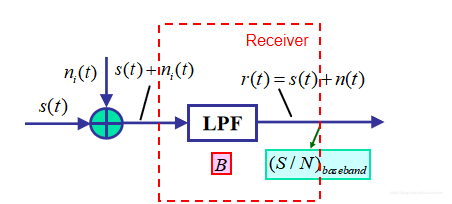
在图7中, m ( t ) m(t) m(t)是带宽为 W W W,功率为 P m P_m Pm的模拟基带信号, s ( t ) s(t) s(t)是带宽为 B B B,功率为 P R P_R PR的已调信号, n ( t ) n(t) n(t)为功率谱密度为 N o 2 \frac{N_o}{2} 2No,带宽为 B T B_T BT的加性高斯白噪声,理想带通滤波器的带宽为 B B B,滤波器的输出信号为:
r ( t ) = s ( t ) + n ( t ) (10) r(t) =s(t)+n(t) \tag{10} r(t)=s(t)+n(t)(10)
本文的抗噪声性能主要考虑解调增益和系统增益,解调增益反应解调器对信噪比的改善能力,系统增益则反映某种调制解调系统相对于统一参照系统的总体增益。
G D E M = ( S N ) o ( S N ) i (11) G_{DEM}=\frac{(\frac{S}{N})_o}{(\frac{S}{N})_i} \tag{11} GDEM=(NS)i(NS)o(11)
G S Y S = ( S N ) o ( S N ) b a s e b a n d = G D E M ∗ B B T (12) G_{SYS}=\frac{(\frac{S}{N})_o}{(\frac{S}{N})_{baseband}}=G_{DEM}*\frac{B}{B_T}\tag{12} GSYS=(NS)baseband(NS)o=GDEM∗BTB(12)
其中, ( S N ) o (\frac{S}{N})_o (NS)o为输出信噪比, ( S N ) i (\frac{S}{N})_i (NS)i为输入信噪比。
( S N ) i = P m N o B T (13) (\frac{S}{N})_i=\frac{P_m}{N_oB_T} \tag{13} (NS)i=NoBTPm(13)
( S N ) o = k 2 m 2 ( t ) ‾ P n (14) (\frac{S}{N})_o=\frac{k^2\overline{m^2(t)}}{P_n}\tag{14} (NS)o=Pnk2m2(t)(14)
k k k反应不同调制方式对消息信号的增益, P n P_n Pn为 n ( t ) n(t) n(t)的功率。
3.1 常规AM模型
常规调幅信号的主要解调方法为包络检波器,即直接提取 s A M ( t ) s_{AM}(t) sAM(t)的实信号来恢复消息信号。当然,也可以通过相干解调来恢复消息信号。
AM已调信号为
s ( t ) = A c c o s 2 π f c t + A c m ( t ) c o s 2 π f c t (15) s(t) = A_ccos2{\pi}f_ct+A_cm(t)cos2{\pi}f_ct \tag{15} s(t)=Accos2πfct+Acm(t)cos2πfct(15)
带宽为 B = 2 W B=2W B=2W,因此借条出的噪声输出功率与DSB-SC相同,设调制效率为 η A M \eta_{AM} ηAM,则信号的功率为 η A M P R \eta_{AM}P_R ηAMPR因此AM如果按照相干解调,其输出信噪比为
( S N ) o = η A M P R N o W = A c 2 m 2 ( t ) ‾ 2 N o B (16) (\frac{S}{N})_o = \eta_{AM}\frac{P_R}{N_oW}=\frac{A_c^2\overline{m^2(t)}}{2N_oB}\tag{16} (NS)o=ηAMNoWPR=2NoBAc2m2(t)(16)
G D E M A M = ( S N ) o ( S N ) i = 2 m 2 ( t ) ‾ 1 + m 2 ( t ) ‾ = 2 η A M (17) G_{DEM_{AM}}= \frac{(\frac{S}{N})_o}{(\frac{S}{N})_i} =\frac{\overline{2m^2(t)}}{1+\overline{m^2(t)}}=2\eta_{AM} \tag{17} GDEMAM=(NS)i(NS)o=1+m2(t)2m2(t)=2ηAM(17)
G S Y S A M = G S Y S A M B 2 B = η A M (18) G_{SYS_{AM}}=G_{SYS_{AM}}\frac{B}{2B}=\eta_{AM}\tag{18} GSYSAM=GSYSAM2BB=ηAM(18)
常规AM的调制效率较低, η A M \eta_{AM} ηAM最大为 1 2 \frac{1}{2} 21,正常情况下,一般低于 1 2 \frac{1}{2} 21,可见,其受噪声干扰大,抗噪声能力较差。
3.2 DSB-SC模型
DSB-SC的已调信号为
s ( t ) = A c m ( t ) c o s 2 π f c t (16) s(t) = A_cm(t)cos2{\pi}f_ct \tag{16} s(t)=Acm(t)cos2πfct(16)
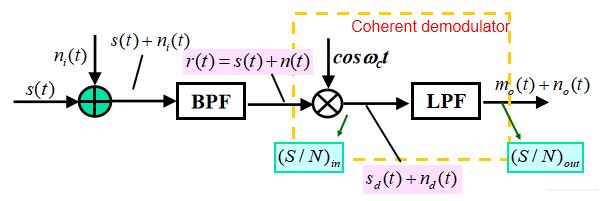
带宽为 B = 2 w B=2w B=2w,功率为 P R = 1 2 A c 2 P m P_R=\frac{1}{2}A_c^2P_m PR=21Ac2Pm。进行数学计算,可以得到:
( S N ) i = 1 2 A c 2 m 2 ( t ) ‾ 2 N o B (17) (\frac{S}{N})_i = \frac{\frac{1}{2}A^2_c\overline{m^2(t)}}{2N_oB} \tag{17} (NS)i=2NoB21Ac2m2(t)(17)
( S N ) o = A c 2 m 2 ( t ) ‾ 2 N o B (18) (\frac{S}{N})_o = \frac{A^2_c\overline{m^2(t)}}{2N_oB} \tag{18} (NS)o=2NoBAc2m2(t)(18)
将式(17),(18)带入式(11),(12)可得
G G E M A M = 2 (19) G_{GEM_{AM}}=2\tag{19} GGEMAM=2(19)
G S Y S A M = G G E M A M B 2 B = 1 (20) G_{SYS_{AM}}=G_{GEM_{AM}}\frac{B}{2B}=1\tag{20} GSYSAM=GGEMAM2BB=1(20)
3.3 单边带调制
对于SSB系统,接收到的有用信号为
s S S B ( t ) = A c m ( t ) c o s 2 π f c t ± A c m ^ ( t ) s i n 2 π f c t (21) s_{SSB}(t)=A_cm(t)cos2{\pi}f_ct{\pm}A_c{\hat{m}(t)sin2{\pi}f_ct} \tag{21} sSSB(t)=Acm(t)cos2πfct±Acm^(t)sin2πfct(21)

由于频谱只有DSB-SC的一半, P S S B = P D S B 2 = 1 4 A c 2 m 2 ( t ) ‾ P_{SSB}=\frac{P_{DSB}}{2}=\frac{1}{4}A^2_c\overline{m^2(t)} PSSB=2PDSB=41Ac2m2(t),输入噪声功率减半,为 N o B N_oB NoB。通过计算可以得到:
( S N ) i = A c 2 m 2 ( t ) ‾ 4 N o B (22) (\frac{S}{N})_i=\frac{A^2_c\overline{m^2(t)}}{4N_oB}\tag{22} (NS)i=4NoBAc2m2(t)(22)
( S N ) o = A c 2 m 2 ( t ) ‾ 4 N o B (23) (\frac{S}{N})_o=\frac{\frac{A^2_c\overline{m^2(t)}}{4}}{N_oB}\tag{23} (NS)o=NoB4Ac2m2(t)(23)
G D E M = 1 (24) G_{DEM}=1 \tag{24} GDEM=1(24)
G S Y S = 1 ∗ B B = 1 (25) G_{SYS}=1*\frac{B}{B}=1 \tag{25} GSYS=1∗BB=1(25)
可见,SSB调制虽然解调增益较低,但系统增益不变,其带宽利用能力更强。
4.仿真结果
在三个模型中,均令 A c = 1 A_c=1 Ac=1, f c = 20 f_c=20 fc=20, m ( t ) = c o s 2 π ∗ 5 t m(t) =cos2{\pi}*5t m(t)=cos2π∗5t, N o = 20 N_o=20 No=20.
4.1 常规AM模型
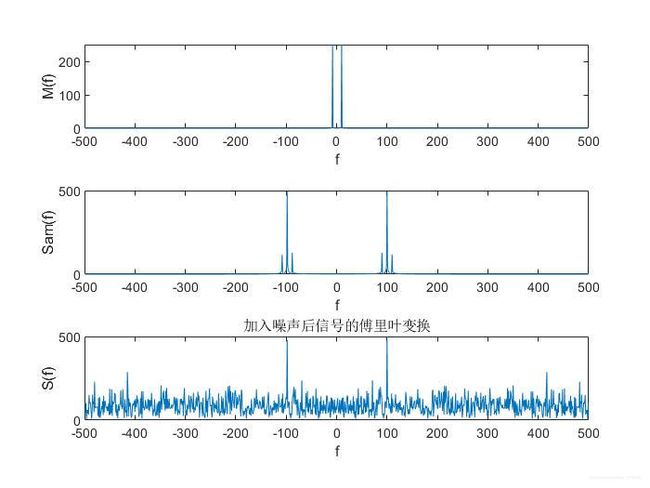

4.2 DSB-SC调制
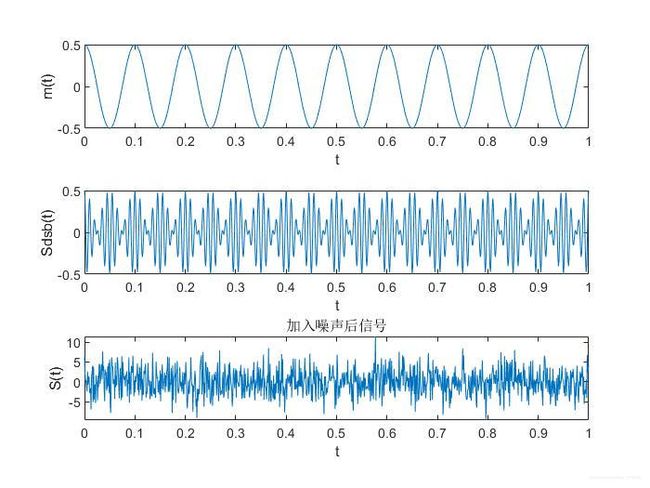
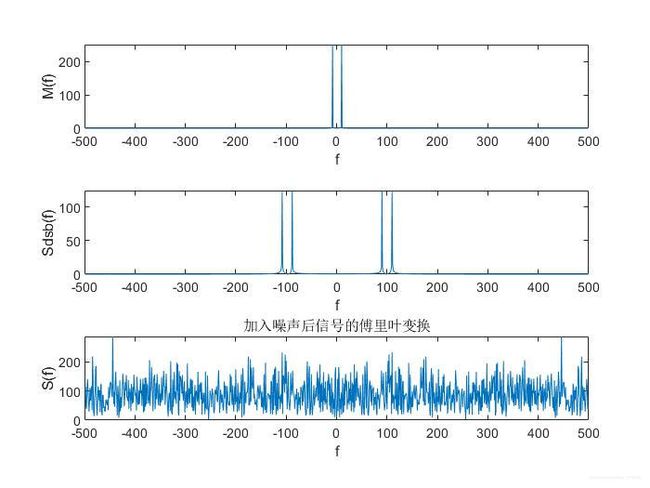

4.3 单边带调制
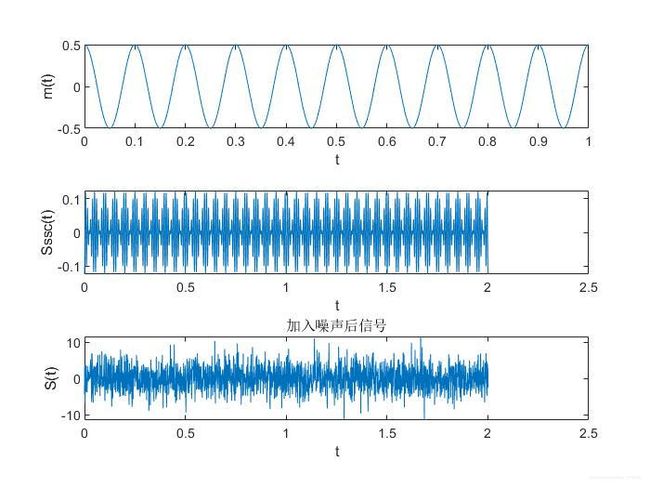
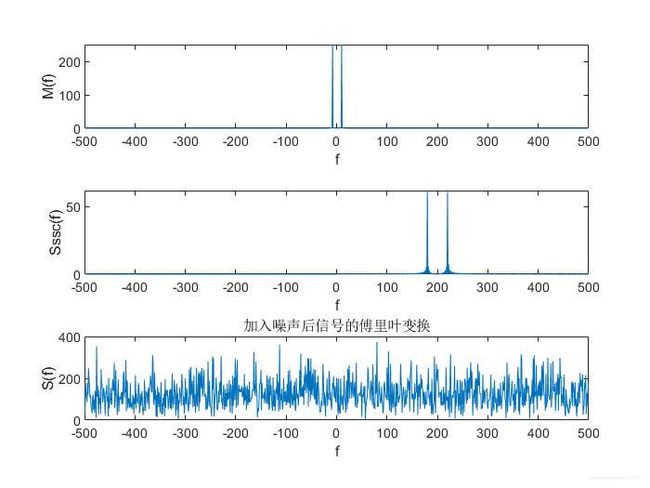

5.小结
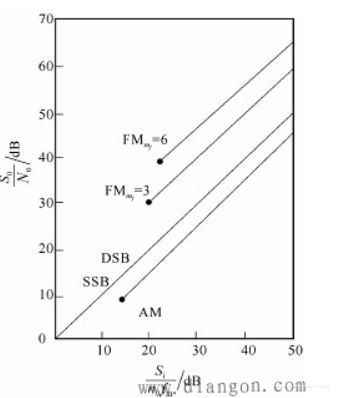
由公式(17),(18),(19),(20),(24)(25)和图20,可以看到,DSB-SC和SSC模拟调制系统具有相同的抗干扰能力,AM抗干扰能力较差。在实际仿真中,三种方案的抗干扰能力都较强,面对 N o N_o No较大的情况均有较好的抗干扰能力。
6.参考文献
[1] 现代通信原理6.2:单边带(SSB)调制
[2] 现代通信原理A.2:FIR低通滤波器设计
[3] 现代通信原理6.1 常规调幅调制(AM)与抑制载波双边带(DSB-SC)调制
[4] 模拟幅度调制系统抗噪声性能仿真分析
[5] 各种模拟调制系统的比较
[6] 【FPGA 】MATLAB 生成 FIR 滤波器的操作步骤(包括生成Verilog HDL代码以及仿真过程)
[7] MATLAB中白噪声的产生
[8] 通信原理(第2版) 李晓峰 周宁 周亮 邵怀宗 朱立东 清华大学出版社
[9] 通信原理(第4版)周炯槃 庞沁华 续大我 吴伟陵 杨鸿文 北京邮电出版社
7.仿真代码
AM仿真
提取包络
DSB-SC仿真
SSB仿真
获取AM和DSB-SC调制的包络