计算机博弈大赛参赛程序算法总结

背景

前两年的全国计算机博弈大赛的爱恩斯坦棋棋种赛我都有参加。14年采用的是极大极小算法，那个时候还不太懂搜索算法的优化，所以算法就是最原始的极大极小搜索，没有做任何剪枝。15年我在上一年的算法基础上加入了Alpha-Beta剪枝，并尝试了一些其他的优化策略，如迭代加深。像其他策略如历史启发、杀手启发之类，都涉及存储中间结点和取出结点，我觉得太过消耗内存，并且有些策略似乎有些鸡肋，不能预见有明显效果。加之极大极小算法本身就是以牺牲内存为代价达到搜索目的，如果采用这样的策略只会加重系统崩溃几率。最后我得到了两个14年程序的改进版本，分别是极大极小+Alpha-Beta剪枝改进版、极大极小+Alpha-Beta剪枝+迭代加深策略改进版。15年暑假时我又阅读了蒙特卡洛搜索算法的相关文献，其中有篇论文《Accelerated UCT and Its Application to Two-Player Games》讲解了蒙特卡洛的先天劣势（总是概率最优，但不是真正最优，而这个概率最优的结点很可能让AI陷入窘境，尤其是在搜索末端这个效应会更加明显），后得到两个蒙特卡洛程序版本，分别是不加改进的蒙特卡洛、加以改进的蒙特卡洛。

感受

爱恩斯坦棋的两个算法方向就是极大极小和蒙特卡洛。前者基于递归，牺牲内存，因而内存成了它最大的制约因素，可以说，只要内存不够，它就没有办法更优。后者基于大量模拟，因而可以采用多线程实现，只要将每次模拟量控制在内存允许范围内，并充分利用规定的时限，则可以发挥比极大极小更大的威力（当然一个很关键的因素是尽量避免蒙特卡洛先天劣势）。

算法细节

0. 形势估计

为了让AI算出棋子的最佳落步，首先必须让AI搞清楚一件事，何为“最佳”？这就牵涉到形势估计。对于极大极小来说，形势估计值可以为双方期望距离之差；对于蒙特卡洛来说，形势估计值可以为模拟胜负率的大小。形势估计函数由程序作者自行设计，没有统一标准。

1. 极大极小

一种很常见的搜索思路是，轮到A下棋，他会选择对自己最有利的；轮到B下棋，他也会选择对自己最有利的。如果用一个参量表示这个“利”，参量越大对A越有利，参量越小对B越有利，于是A下棋时这个参量特别大，B下棋时这个参量特别小，由于A、B是交互下棋，于是这个参量在搜索层间就呈现出“一会儿特别大一会儿特别小”的状态。
伪代码（来自维基百科）：

function minimax(node, depth) // 指定当前节点和搜索深度
   // 如果能得到确定的结果或者深度为零，使用评估函数返回局面得分
   if node is a terminal node or depth = 0
       return the heuristic value of node
   // 如果轮到对手走棋，是极小节点，选择一个得分最小的走法
   if the adversary is to play at node
       let α := +∞
       foreach child of node
           α := min(α, minimax(child, depth-1))
   // 如果轮到我们走棋，是极大节点，选择一个得分最大的走法   else {we are to play at node}
       let α := -∞
       foreach child of node
           α := max(α, minimax(child, depth-1))
   return α;

2. Alpha-Beta剪枝

如果用最简洁的话说明Alpha-Beta剪枝，那就是“不要耗费精力搜索那些可以预见的无用的结点”。这里以Alpha剪枝为例进行说明：

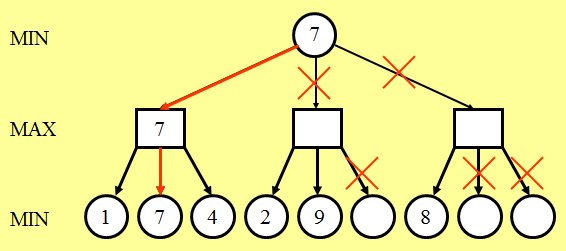
这里起始结点为极大结点，它的形势值为 max(子结点形势值) 。而它的下一层都为极小结点，它们各自的形势值为 min(各自的子结点形势值) 。Alpha剪枝过程：
a. 深度搜索起始结点的左子树后，起始结点的形势值更新为4
b. 深度搜索起始结点的中间子树，当起始结点的中间子结点的形势值更新为2时，此时可预见，中间子结点的形势值<=2，所以没必要再继续搜索起始结点的中间子树了，毕竟中间子结点的形势值永远劣于4.
c.同理，当深度搜索起始结点的右子树时，右子树的左结点返回的形势值为3，因而右子树的形势值<=3，同样也没有了继续搜索的必要。
Beta剪枝类似于Alpha剪枝，只不过它的起始结点为极小结点罢了。如图：

Alpha-Beta算法伪代码如下：

function alphabeta(node, depth, α, β, Player)         
    if  depth = 0 or node is a terminal node
        return the heuristic value of node
    if  Player = MaxPlayer // 极大节点
        for each child of node // 极小节点
            α := max(α, alphabeta(child, depth-1, α, β, not(Player) ))   
            if β ≤ α 
                break                             (* Beta cut-off *)
        return α
    else // 极小节点
        for each child of node // 极大节点
            β := min(β, alphabeta(child, depth-1, α, β, not(Player) )) // 极小节点
            if β ≤ α
                break                             (* Alpha cut-off *)
        return β 
(* Initial call *)
alphabeta(origin, depth, -∞, +∞, MaxPlayer)

3. 迭代加深策略

迭代加深最核心的思想就是“充分利用比赛时间”。因为在比赛的初始阶段，双方棋子较多，搜索比较耗时，也比较吃内存，这时AI能够搜索的层数比较有限。随着比赛进行，双方棋子不断减少，相应地，AI可以搜索更多的层数。如果把搜索层数限制成一个定数，那么越到比赛末期，越有大把的比赛时间给白白浪费掉。迭代加深是一种试探性的搜索，先搜索一定层数，如果发现时间还有结余，就多搜索几层（通常是一层，毕竟每多一层结点数将爆炸性增长）。伪代码如下：

while {
　val = AlphaBeta(origin, depth, -∞, +∞, MaxPlayer);
　if (TimedOut()) {
　　break;
　}
}

4. 蒙特卡洛

蒙特卡洛算法的特征是“基于大量的随机的模拟”，意思是AI在搜索过程中，所有的棋步都是随机产生的。当轮到A下时，A的落棋随机产生，当轮到B下时，B的落棋也随机产生，直到该盘胜负已定。假如现在AI要判断出A的最佳走步，而A当前有三个可以走的棋步，于是AI对这三个走步情况进行大量随机模拟，发现其中某个走步的胜率最高，所以这个走步是最优的。
蒙特卡洛的实现比较简单，只要掌握多线程编程技术，编写好模拟规则，再写个随机数生成器即可。
关于蒙特卡洛的劣势：

如图所示，在D或E或H后，无论如何都是player1赢；在F或I后，无论如何都是player2赢。于是乎，AI会认为，A结点如果下一步走B结点，胜率会最大。可是，一旦走B，而player2走F，则player1势必会输。而如果A结点下一步走C结点，则player2就只能G结点，此时player1再走I结点则必胜。蒙特卡洛在概率学上是最优的，可是正如上图所示，它未必是最优的。因此如果要对蒙特卡洛做一点小小的改进的话，可以从这里入手（如如果某个结点可以直接决定胜负，则忽略它的兄弟结点）。