【从线性回归到BP神经网络】第二部分:线性回归
文章目录
- 1、代价函数
- 2、梯度下降法
- 3、线性回归的梯度下降
- 4、矩阵形式表示 m m m个样本
- 5、线性回归的闭式解
- 6、从概率的角度来理解代价函数
本文主要参考文献如下:
1、吴恩达CS229课程讲义。
2、(美)S.Chatterjee等,《例解回归分析》(第2章),机械工业出版社。
3、周志华. 《机器学习》3.2.清华大学出版社。
4、(美)P.Harrington,《机器学习实战》人民邮电出版社。
1、代价函数
我们先考虑只有单个数据对的情况,即 x = [ 1 , x 1 , x 2 , … , x n ] {\bf x}=[1,x_1,x_2,\ldots,x_n] x=[1,x1,x2,…,xn]为输入的属性向量,其中 n n n为属性的个数, y y y为与 x \bf x x对应的输出函数值。我们希望能够用 x \bf x x的线性函数来预测 y y y的值,即
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + … + θ n x n = ∑ j = 1 n θ j x j = θ T x , (1) \tag{1} \begin{aligned} h_{\theta}({\bf x})&=\theta_0+\theta_1x_1+\theta_2x_2+\ldots+\theta_nx_n\\ &=\sum_{j=1}^{n}\theta_jx_j\\ &={\bm \theta}^{\rm T}{\bf x}, \end{aligned} hθ(x)=θ0+θ1x1+θ2x2+…+θnxn=j=1∑nθjxj=θTx,(1)这里, θ = [ θ 0 , θ 1 , … , θ n ] T {\bm \theta}=[\theta_0,\theta_1,\ldots,\theta_n]^{\rm T} θ=[θ0,θ1,…,θn]T为参数向量。显然,我们希望通过选择合适的参数 θ {\bm \theta} θ,使得 h θ ( x ) h_{\bm \theta}({\bf x}) hθ(x)能够尽量接近 y y y的值。
那么如何来定义“接近”的程度呢?采用的就是cost function(代价函数)。常用的一种cost function的定义,就是均方值
J ( θ ) = 1 2 [ h θ ( θ ) − y ] 2 (2) \tag{2} J(\bm \theta)=\frac{1}{2}[h_{\theta}({\bm \theta})-y]^2 J(θ)=21[hθ(θ)−y]2(2)我们推广到有 m m m个数据对的情况,此时的代价函数为
J ( θ ) = 1 2 m ∑ i = 1 m [ h θ ( x ( i ) ) − y ( i ) ] 2 . (3) \tag{3} J(\bm \theta)=\frac{1}{2m}\sum_{i=1}^{m}[h_{\theta}({{\bf x}^{(i)}})-y^{(i)}]^2. J(θ)=2m1i=1∑m[hθ(x(i))−y(i)]2.(3)
严格来说,根据第一部分,这里的分母的 m m m应该为 m − 1 m-1 m−1。
2、梯度下降法
多元函数 J ( θ ) J(\bm \theta) J(θ)的值会随着 θ \bm \theta θ的改变而改变。我们希望能够尽快找到使 J ( θ ) J(\theta) J(θ)最小的 θ \bm \theta θ,那么 θ \bm \theta θ应该往哪个方向变化, J ( θ ) J(\bm \theta) J(θ)的值能够下降得更快呢?
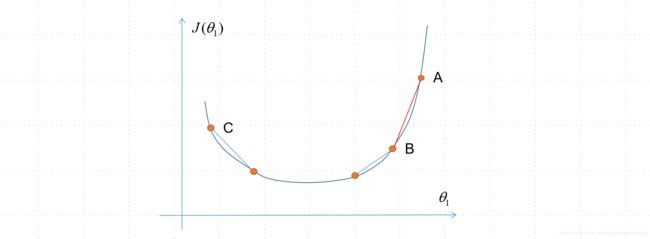
首先我们看”方向”这个词的含义。这里的方向,其实就是指每个参数, θ j \theta_j θj,第一是变大还是变小(正 or 负),第二是变得快还是慢。以下图一维的情况来看,显然A点切线斜率比B点的大,因此下降得更快,而C点 θ 1 \theta_1 θ1得值应该增大,而非减小。想象下如果换成多维情况,其实就是看每个参数应该变大还是变小,应该以多快速率变化(在学习率 α \alpha α一定的情况下)。如果想象从山顶往山下走(两个参数的情况),显然两个参数的正负和变化快慢,决定了下山路线的方向。
梯度下降法实际上就是选择下降最快方向的方法,即
θ j : = θ j − α ∂ J ( θ ) ∂ θ j j = 0 , 1 , … , n . (4) \tag{4} \theta_j:=\theta_j-\alpha\frac{\partial J(\bm \theta)}{\partial \theta_j}\quad j=0,1,\ldots,n. θj:=θj−α∂θj∂J(θ)j=0,1,…,n.(4)
注意梯度下降法的特点:
- 梯度(切线斜率)越大,下降越快; 梯度越小,下降越慢。
- 如果到了局部最优点(斜率为0),则不再变化。
- 所有 θ j \theta_j θj的值要同时更新。
3、线性回归的梯度下降
回到我们的问题上来。我们是想找到(3)中代价函数的最小值,因此到我们设置好 θ \bm \theta θ的初始值之后,就开始用(4)更新 θ \theta θ值,逐渐逼近最优点。因此我们需要求得梯度,即
∂ J ( θ ) ∂ θ j = 1 2 m ∂ ∂ θ j ∑ i = 1 m [ h θ ( x ( i ) ) − y ( i ) ] 2 = 1 2 m ∂ ∂ θ j ∑ i = 1 m [ ∑ j = 1 n θ j x j ( i ) − y ( i ) ] 2 = 1 m ∑ i = 1 m [ ∑ j = 1 n θ j x j ( i ) − y ( i ) ] ⋅ x j ( i ) = 1 m ∑ i = 1 m [ h θ ( x ( i ) ) − y ( i ) ] ⋅ x j ( i ) (5) \tag{5} \begin{aligned} \frac{\partial J({\bm \theta}) }{\partial \theta_j }&=\frac{1}{2m}\frac{\partial }{\partial \theta_j }\sum_{i=1}^{m}[h_{\theta}({{\bf x}^{(i)}})-y^{(i)}]^2\\ &=\frac{1}{2m}\frac{\partial }{\partial \theta_j }\sum_{i=1}^{m}[\sum_{j=1}^{n}\theta_jx_j^{(i)}-y^{(i)}]^2\\ &=\frac{1}{m}\sum_{i=1}^{m}[\sum_{j=1}^{n}\theta_jx_j^{(i)}-y^{(i)}]\cdot x_j^{(i)}\\ &=\frac{1}{m}\sum_{i=1}^{m}[h_{\theta}{({\bf x}^{(i)})}-y^{(i)}]\cdot x_j^{(i)}\\ \end{aligned} ∂θj∂J(θ)=2m1∂θj∂i=1∑m[hθ(x(i))−y(i)]2=2m1∂θj∂i=1∑m[j=1∑nθjxj(i)−y(i)]2=m1i=1∑m[j=1∑nθjxj(i)−y(i)]⋅xj(i)=m1i=1∑m[hθ(x(i))−y(i)]⋅xj(i)(5)
4、矩阵形式表示 m m m个样本
为了编程实现时候方便,我们来看如何用矩阵形式同时处理 m m m个数据。我们可以得到 X = [ x ( 1 ) T x ( 2 ) T ⋮ x ( m ) T ] ∈ R m × ( 1 + n ) , y = [ y ( 1 ) y ( 2 ) ⋮ y ( m ) ] ∈ R m × 1 , θ = [ θ 0 θ 1 ⋮ θ n ] ∈ R ( n + 1 ) × 1 (6) \tag{6} {\bf X}=\left[\begin{aligned} {\bf x}^{{(1)}\rm T}\\ {\bf x}^{{(2)}\rm T}\\ \vdots\\ {\bf x}^{{(m)}\rm T}\\ \end{aligned} \right]\in {\mathbb R}^{m\times (1+n)},{\bf y}=\left[\begin{aligned} { y}^{{(1)}}\\ { y}^{{(2)}}\\ \vdots\\ { y}^{{(m)}}\\ \end{aligned} \right]\in {\mathbb R}^{m\times 1},{\bm \theta}=\left[\begin{aligned} \theta_0\\ \theta_1\\ \vdots\\ \theta_n\\ \end{aligned} \right]\in {\mathbb R}^{(n+1)\times 1} X=⎣⎢⎢⎢⎢⎢⎡x(1)Tx(2)T⋮x(m)T⎦⎥⎥⎥⎥⎥⎤∈Rm×(1+n),y=⎣⎢⎢⎢⎢⎢⎡y(1)y(2)⋮y(m)⎦⎥⎥⎥⎥⎥⎤∈Rm×1,θ=⎣⎢⎢⎢⎢⎢⎡θ0θ1⋮θn⎦⎥⎥⎥⎥⎥⎤∈R(n+1)×1(6)因此,有估计值为
y ^ = [ y ^ ( 1 ) y ^ ( 2 ) ⋮ y ^ ( m ) ] = X θ (7) \tag{7} \hat {\bf y}=\left[\begin{aligned} {\hat y}^{{(1)}}\\ {\hat y}^{{(2)}}\\ \vdots\\ {\hat y}^{{(m)}}\\ \end{aligned} \right]={\bf X}{\bm \theta} y^=⎣⎢⎢⎢⎢⎢⎡y^(1)y^(2)⋮y^(m)⎦⎥⎥⎥⎥⎥⎤=Xθ(7)由此可以得到代价函数为
J ( θ ) = 1 2 m ∥ y − y ^ ∥ 2 = 1 2 m ( y − X θ ) T ( y − X θ ) (8) \tag{8} \begin{aligned} J({\bm \theta})&=\frac{1}{2m}\| {\bf y}-\hat{\bf y}\|^2\\ &=\frac{1}{2m}({\bf y}-{\bf X}{\bm \theta})^{\rm T}({\bf y}-{\bf X}{\bm \theta}) \end{aligned} J(θ)=2m1∥y−y^∥2=2m1(y−Xθ)T(y−Xθ)(8)因此, θ \bm \theta θ更新如下
θ : = θ − 1 m [ α ( y − y ^ ) T X ] T j = 0 , 1 , … , n (9) \tag{9} {\bm \theta}:={\bm \theta}-\frac{1}{m}[\alpha({\bf y}-\hat {\bf y})^{\rm T}{\bf X}]^{\rm T}\quad j=0,1,\ldots,n θ:=θ−m1[α(y−y^)TX]Tj=0,1,…,n(9)
也就是说,对于输入的 m m m组特征样本 X \bf X X,我们先根据(7)在现有 θ \bm \theta θ情况下估计输出 y ^ \hat y y^,然后根据(9)来更新 θ \bm \theta θ。下面是一段MATLAB代码。
%学习过程
for cnt=1:N_Loop
hat_yy=X_Train*theta; %根据(7)估计输出
tmp1=yy_Train-hat_yy;
theta=theta+(alpha*tmp1'*X_Train/m)'; %根据(9)更新参数
end
5、线性回归的闭式解
除了采用梯度下降法,我们也可以对下面的优化问题寻求闭式解,即
θ ^ ∗ = min θ J ( θ ) (10) \tag{10} {\hat \bm \theta}^*=\min \limits_{\bm \theta} J(\bm \theta) θ^∗=θminJ(θ)(10)根据(8),可以将该优化问题表示为
θ ^ ∗ = min θ ∥ y − y ^ ∥ 2 . (11) \tag{11} {\hat \bm \theta}^*=\min \limits_{\bm \theta} \| {\bf y}-\hat{\bf y}\|^2. θ^∗=θmin∥y−y^∥2.(11)进一步,由于
∥ y − y ^ ∥ 2 = ( y − X θ ) T ( y − X θ ) \| {\bf y}-\hat{\bf y}\|^2=({\bf y}-{\bf X}{\bm \theta})^{\rm T}({\bf y}-{\bf X}{\bm \theta}) ∥y−y^∥2=(y−Xθ)T(y−Xθ)对其求导,可以得到
∂ ∂ θ ∥ y − y ^ ∥ 2 = ∂ ∂ θ ( y − X θ ) T ( y − X θ ) = 2 X T ( X θ − y ) ∈ R (12) \tag{12} \begin{aligned} \frac{\partial}{\partial \bm \theta} \| {\bf y}-\hat{\bf y}\|^2&=\frac{\partial}{\partial \bm \theta}({\bf y}-{\bf X}{\bm \theta})^{\rm T}({\bf y}-{\bf X}{\bm \theta})\\ &=2{\bf X}^{\rm T}({\bf X}{\bm \theta}-{\bf y})\in{\mathbb R}_{}^{} \end{aligned} ∂θ∂∥y−y^∥2=∂θ∂(y−Xθ)T(y−Xθ)=2XT(Xθ−y)∈R(12)
我们考虑有向量 x ∈ R n × 1 {\bf x}\in {\mathbb R}^{n\times 1} x∈Rn×1的标量函数 f ( x ) f(\bf x) f(x)为
f ( x ) = x T x = x 1 2 + x 2 2 + … + x n 2 f({\bf x})={\bf x}^{\rm T}{\bf x}=x_1^2+x_2^2+\ldots+x_n^2 f(x)=xTx=x12+x22+…+xn2则其相对于 x \bf x x的梯度(导数)为列向量
∂ f ( x ) ∂ x = [ ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , … , ∂ f ( x ) ∂ x n ] T = 2 x \begin{aligned} \frac{\partial f({\bf x})}{\partial {\bf x}}&=\left[\frac{\partial f({\bf x})}{\partial {x_1}},\frac{\partial f({\bf x})}{\partial {x_2}},\ldots,\frac{\partial f({\bf x})}{\partial {x_n}}\right]^{\rm T}\\ &=2{\bf x} \end{aligned} ∂x∂f(x)=[∂x1∂f(x),∂x2∂f(x),…,∂xn∂f(x)]T=2x若 X ∈ R m × n {\bf X}\in {\mathbb R}^{m\times n} X∈Rm×n, θ ∈ R n × 1 {\bm \theta}\in {\mathbb R}^{n\times 1} θ∈Rn×1,下面我们再来看 1 × m 1\times m 1×m行向量
z = ( X θ ) T = θ T X T \begin{aligned} {\bf z}&=({\bf X}{\bm \theta})^{\rm T}={\bm \theta}^{\rm T}{\bf X}^{\rm T}\\ \end{aligned} z=(Xθ)T=θTXT相对于 n × 1 n\times 1 n×1列向量 θ \bm \theta θ求导,显然求导后为 n × m n \times m n×m矩阵,即
∂ z ∂ θ = X T \begin{aligned} \frac{\partial {\bf z}}{\partial {\bm \theta}}&={\bf X}^{\rm T} \end{aligned} ∂θ∂z=XT
令(12)等于零,就可以得到 θ \bm \theta θ最优解的闭式解,即
X T ( X θ − y ) = 0 (13) \tag{13} \begin{aligned} {\bf X}^{\rm T}({\bf X}{\bm \theta}-{\bf y})=0 \end{aligned} XT(Xθ−y)=0(13) 若 X T X {\bf X}^{\rm T}{\bf X} XTX满秩,可以得到
θ ^ ∗ = ( X T X ) − 1 X T y . (14) \tag{14} {\hat \bm \theta}^*=({\bf X}^{\rm T}{\bf X})^{-1}{\bf X}^{\rm T}{\bf y}. θ^∗=(XTX)−1XTy.(14)
显然(9)的梯度下降法和(14)的闭式解,都可以求得使得代价函数 J J J最小的参数 θ \bm \theta θ值。经常用梯度算法代替闭式解的原因,是如果数据量比较大,求解矩阵运算的计算量会太大。
一般来说,我们会采用相关系数来评价回归性能,相关系数定义见第一部分。
6、从概率的角度来理解代价函数
下面我们从概率的角度来分析,为什么我们选择用均方误差 ∥ y − y ^ ∥ \|{\bf y}-\hat{\bf y}\| ∥y−y^∥作为代价函数(即LMS算法)是合理的。
我们先来考虑单个数据的情况。对于第 i i i个数据,有
y ( i ) = θ T x ( i ) + ϵ ( i ) , (15) \tag{15} y^{(i)}={\bm \theta}^{\rm T}{\bf x}^{(i)}+\epsilon^{(i)}, y(i)=θTx(i)+ϵ(i),(15)这里 ϵ ( i ) ∼ N ( 0 , σ 2 ) \epsilon^{(i)}\sim {\mathcal N}(0,\sigma^2) ϵ(i)∼N(0,σ2)为误差项。因此,我们可以得到 y ( i ) y^{(i)} y(i)的条件概率为
p ( y ( i ) ∣ x ( i ) ; θ ) = 1 2 π σ exp ( − [ y ( i ) − θ T x ( i ) ] 2 2 σ 2 ) (16) \tag{16} p(y^{(i)}|{\bf x}^{(i)};{\bm \theta})=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{[y^{(i)}-{\bm \theta}^{\rm T}{\bf x}^{(i)}]^2}{2\sigma^2}\right) p(y(i)∣x(i);θ)=2πσ1exp(−2σ2[y(i)−θTx(i)]2)(16)注意这里 θ \bm \theta θ是参数而非随机变量。
下面来考虑多个样本数据的情况。对于固定的 θ \bm \theta θ,在给定 X \bf X X的情况下, y \bf y y的概率密度函数,我们称之为似然函数,为
L ( θ ) = ∏ i = 1 m p ( y ( i ) ∣ x ( i ) ; θ ) = ∏ i = 1 m 1 2 π σ exp ( − [ y ( i ) − θ T x ( i ) ] 2 2 σ 2 ) . (17) \tag{17}\begin{aligned} L({\bm \theta})&=\prod_{i=1}^{m}p(y^{(i)}|{\bf x}^{(i)};{\bm \theta})\\ &=\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{[y^{(i)}-{\bm \theta}^{\rm T}{\bf x}^{(i)}]^2}{2\sigma^2}\right). \end{aligned} L(θ)=i=1∏mp(y(i)∣x(i);θ)=i=1∏m2πσ1exp(−2σ2[y(i)−θTx(i)]2).(17)下面我们用最大似然准则,这意味着我们选择使得(17)中似然函数最大的 θ \bm \theta θ。事实上,我们也可以最大化似然函数的某个严格单调递增的函数,比如对数似然,显然可以把连乘运算变成连加运算
ℓ ( θ ) = log L ( θ ) = log ∏ i = 1 m 1 2 π σ exp ( − [ y ( i ) − θ T x ( i ) ] 2 2 σ 2 ) = ∑ i = 1 m log 1 2 π σ exp ( − [ y ( i ) − θ T x ( i ) ] 2 2 σ 2 ) = m log 1 2 π − 1 2 σ 2 ∑ i = 1 m [ y ( i ) − θ T x ( i ) ] 2 (18) \tag{18} \begin{aligned} \ell(\bm \theta)&=\log L(\bm \theta)\\ &=\log \prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{[y^{(i)}-{\bm \theta}^{\rm T}{\bf x}^{(i)}]^2}{2\sigma^2}\right)\\ &=\sum_{i=1}^{m}\log\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{[y^{(i)}-{\bm \theta}^{\rm T}{\bf x}^{(i)}]^2}{2\sigma^2}\right)\\ &=m\log\frac{1}{\sqrt{2\pi}}-\frac{1}{2\sigma^2}\sum_{i=1}^{m}[y^{(i)}-{\bm \theta}^{\rm T}{\bf x}^{(i)}]^2 \end{aligned} ℓ(θ)=logL(θ)=logi=1∏m2πσ1exp(−2σ2[y(i)−θTx(i)]2)=i=1∑mlog2πσ1exp(−2σ2[y(i)−θTx(i)]2)=mlog2π1−2σ21i=1∑m[y(i)−θTx(i)]2(18)因此,最大化 ℓ ( θ ) \ell(\bm \theta) ℓ(θ)事实上就是最小化
1 2 ∑ i = 1 m [ y ( i ) − θ T x ( i ) ] 2 (19) \tag{19} \frac{1}{2}\sum_{i=1}^{m}[y^{(i)}-{\bm \theta}^{\rm T}{\bf x}^{(i)}]^2 21i=1∑m[y(i)−θTx(i)]2(19)即(3)中的均方差。