【从线性回归到BP神经网络】第三部分：Logistic回归

本文主要参考文献如下：
1、吴恩达CS229课程讲义。
2、（美）S.Chatterjee等，《例解回归分析》（第2章），机械工业出版社。
3、周志华. 《机器学习》3.2.清华大学出版社。
4、（美）P.Harrington，《机器学习实战》人民邮电出版社。
5、陈明等，《MATLAB神经网络原理与实例精解》，清华大学出版社。

1、 Logistic函数

  下面我们来考虑如何将线性回归用于二分类问题。显然，经过线性回归之后的输出
$$\hat{y}=h_{\mathbf{\theta }}(\mathbf{x})={\mathbf{\theta }}^{\mathrm{T}}\mathbf{x}$$是实数。如果$y\in [0,1]$，显然我们需要改变$h_{\mathbf{\theta }}(\mathbf{x})$使其值也在0到1之间。这里我们采用Logistic函数，或者也叫Sigmoid函数如下：
$$h_{\mathbf{\theta }}(\mathbf{x})=g({\mathbf{\theta }}^{\mathrm{T}}\mathbf{x})=\frac{1}{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}.\text{\hspace{1em}(1)}$$它的图形如图1所示。

图1 Sigmoid函数图形

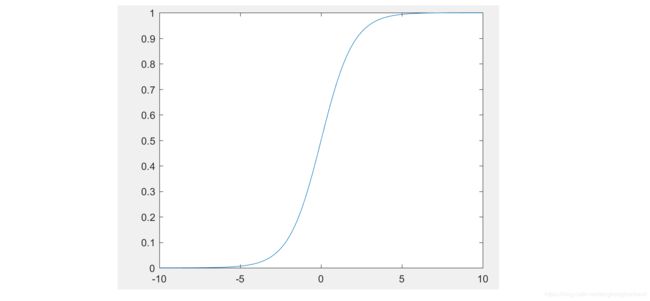
Sigmoid函数$g(z)$有一个很重要的性质，就是它的微分
$$g^{\prime }(z)=g(z)[1-g(z)].\text{\hspace{1em}(2)}$$

我们来推导(2)。
$$\begin{array}{rl}{g}^{\prime }(z)& =\frac{d}{dz}\frac{1}{1+e^{-z}}\\ & =\frac{1}{(1+e^{-z}{)}^2}(e^{-z})\\ & =\frac{1}{(1+e^{-z})}\cdot \left(1-\frac{1}{1+e^{-z}}\right)\\ & =g(z)[1-g(z)]\end{array}$$

2、最大似然函数准则

  这里我们考虑二分类问题。由于$y$的取值为0或者1，因此我们需要根据$h_{\mathbf{\theta }}(\mathbf{x})$来猜测，到底输出$\hat{\mathbf{y}}$为0还是1呢？由于$h_{\mathbf{\theta }}(\mathbf{x})$的值在0到1之间，我们就用它作为概率值，即
$$\begin{array}{rl}P(y=1|\mathbf{x};\mathbf{\theta })& =h_{\mathbf{\theta }}(\mathbf{x})\\ P(y=0|\mathbf{x};\mathbf{\theta })& =1-h_{\mathbf{\theta }}(\mathbf{x})\end{array}\text{\hspace{1em}(3)}$$

我们从图2可以看出(3)的假设是合理的。如果Sigmoid函数的输入${\mathbf{\theta }}^{\mathrm{T}}\mathbf{x}$大于0，则$h_{\mathbf{\theta }}(\mathbf{x})$大于0.5，这意味着$\hat{\mathbf{y}}$为1(>0)的可能性更大；反之，如果${\mathbf{\theta }}^{\mathrm{T}}\mathbf{x}$小于0，则$h_{\mathbf{\theta }}(\mathbf{x})$小于0.5，这意味着$\hat{\mathbf{y}}$为0(<0)的可能性更大。

由于$y$是二值离散随机变量，我们可以得到它的条件概率密度函数为
$$p(y|\mathbf{x};\mathbf{\theta })=[h_{\mathbf{\theta }}(\mathbf{x}){]}^y[1-h_{\mathbf{\theta }}(\mathbf{x}){]}^{1-y}\text{\hspace{1em}(4)}$$假定$m$个样本彼此独立，我们得到关于参数$\mathbf{\theta }$的似然函数为
$$L(\mathbf{\theta })=\prod _{i=1}^m[h_{\mathbf{\theta }}({\mathbf{x}}^{(i)}){]}^{y^{(i)}}[1-h_{\mathbf{\theta }}({\mathbf{x}}^{(i)}){]}^{1-y^{(i)}}\text{\hspace{1em}(5)}$$对数似然函数为
$$\ell (\mathbf{\theta })=\sum _{i=1}^m{y}^{(i)}\log h_{\mathbf{\theta }}({\mathbf{x}}^{(i)})+(1-y^{(i)})\log [1-h_{\mathbf{\theta }}({\mathbf{x}}^{(i)})]\text{\hspace{1em}(6)}$$

3、用梯度下降法来最大化对数似然

  现在的优化问题变成
$${\hat{\mathbf{\theta }}}^{\ast }=\underset{\mathbf{\theta }}{\max }\ell (\mathbf{\theta }).\text{\hspace{1em}(7)}$$与线性回归类似，我们用梯度法来求解，即找到让$\ell (\mathbf{\theta })$变化最快的方向（梯度），从而更新参数
$$\mathbf{\theta }:=\mathbf{\theta }+\alpha {▽}_{\mathbf{\theta }}\ell (\mathbf{\theta })\text{\hspace{1em}(8)}$$注意由于求解最大值，上式中用的是加号而非减号。
  我们先来求单个样本时的梯度。对于
$$\ell (\mathbf{\theta })=y\log h_{\mathbf{\theta }}(\mathbf{x})+(1-y)\log [1-h_{\mathbf{\theta }}(\mathbf{x})]\text{\hspace{1em}(9)}$$若$j=0,1,2\dots ,n$，由于$h_{\mathbf{\theta }}(\mathbf{x})=g({\mathbf{\theta }}^{\mathrm{T}}\mathbf{x})$，有
$$\begin{array}{rl}\frac{\partial }{\partial {\theta }_j}\ell (\theta )& =\left[\frac{y}{g({\mathbf{\theta }}^{\mathrm{T}}\mathbf{x})}-\frac{(1-y)}{1-g({\mathbf{\theta }}^{\mathrm{T}}\mathbf{x})}\right]\frac{\partial g({\mathbf{\theta }}^{\mathrm{T}}\mathbf{x})}{\partial {\theta }_j}\\ & =\left[\frac{y}{g({\mathbf{\theta }}^{\mathrm{T}}\mathbf{x})}-\frac{(1-y)}{1-g({\mathbf{\theta }}^{\mathrm{T}}\mathbf{x})}\right]g({\mathbf{\theta }}^{\mathrm{T}}\mathbf{x})[1-g({\mathbf{\theta }}^{\mathrm{T}}\mathbf{x})]\cdot \frac{\partial {\sum }_{j=0}^n{\theta }_j{x}_j}{\partial {\theta }_j}\\ & =(y-h_{\mathbf{\theta }}(\mathbf{x}))x_j\end{array}\text{\hspace{1em}(10)}$$因此，我们可以得到参数$\mathbf{\theta }$的更新准则为
$$\begin{array}{r}{\theta }_j:={\theta }_j+\alpha \cdot (y^{(i)}-h_{\mathbf{\theta }}({\mathbf{x}}^{(i)}))x_j^{(i)},j=0,1,\dots ,n\end{array}\text{\hspace{1em}(11)}$$我们可以用矩阵形式表示为
$$\mathbf{\theta }:=\mathbf{\theta }+[\alpha (\mathbf{y}-\hat{\mathbf{y}}{)}^{\mathrm{T}}\mathbf{X}{]}^{\mathrm{T}}\text{\hspace{1em}(12)}$$其中$\hat{\mathbf{y}}=[{\hat{y}}_1,{\hat{y}}_2,\dots ,{\hat{y}}_m{]}^{\mathrm{T}}$，${\hat{y}}_i=h_{\mathbf{\theta }}({\mathbf{x}}^{(i)})$。