【数据挖掘导论】读书笔记 - (1)
解决方案:
数据预处理:
小知识复习:正太分布
(1)聚集
(2)抽样
(3)维归约
(4)特征子集选择
(5)特征创建
(6)离散化和二元化
转自: http://book.51cto.com/art/201011/235430.htm
有些数据挖掘算法,特别是某些分类算法,要求数据是分类属性形式。发现关联模式的算法要求数据是二元属性形式。这样,常常需要将连续属性变换成分类属性(离散化,discretization),并且连续和离散属性可能都需要变换成一个或多个二元属性(二元化,binarization)。此外,如果一个分类属性具有大量不同值(类别),或者某些值出现不频繁,则对于某些数据挖掘任务,通过合并某些值减少类别的数目可能是有益的。与特征选择一样,最佳的离散化和二元化方法是"对于用来分析数据的数据挖掘算法,产生最好结果"的方法。直接使用这种判别标准通常是不实际的。因此,离散化和二元化一般要满足这样一种判别标准,它与所考虑的数据挖掘任务的性能好坏直接相关。
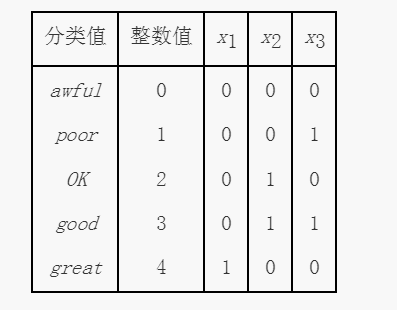
这样的变换可能导致复杂化,如无意之中建立了转换后的属性之间的联系。例如,在表2-5中,属性x2和x3是相关的,因为good值使用这两个属性表示。此外,关联分析需要非对称的二元属性,其中只有属性的出现(值为1)才是重要的。因此,对于关联问题,需要为每一个分类值引入一个二元属性,如表2-6所示。如果结果属性的个数太多,则可以在二元化之前使用下面介绍的技术减少分类值的个数。转换见表

同样,对于关联问题,可能需要用两个非对称的二元属性替换单个二元属性。考虑记录人的性别(男、女)的二元属性,对于传统的关联规则算法,该信息需要转换成两个非对称的二元属性,其中一个仅当是男性时为1,而另一个仅当是女性时为1。(对于非对称的二元属性,由于其提供一个二进制位信息需要占用存储器的两个二进制位,因而在信息的表示上不太有效。)
通常,离散化应用于在分类或关联分析中使用到的属性上。一般来说,离散化的效果取决于所使用的算法,以及用到的其他属性。然而,属性离散化通常单独考虑。
连续属性变换成分类属性涉及两个子任务:决定需要多少个分类值,以及确定如何将连续属性值映射到这些分类值。在第一步中,将连续属性值排序后,通过指定n 1个分割点(split point)把它们分成n个区间。在颇为平凡的第二步中,将一个区间中的所有值映射到相同的分类值。因此,离散化问题就是决定选择多少个分割点和确定分割点位置的问题。结果可以用区间集合{(x0, x1], (x1, x2],..., (xn-1, xn)}表示,其中x0和xn可以分别为- 或+ ,或者用一系列不等式x0 < x≤x1,..., xn-1 < x < xn表示。
非监督离散化 用于分类的离散化方法之间的根本区别在于使用类信息(监督,supervised)还是不使用类信息(非监督,unsupervised)。如果不使用类信息,则常使用一些相对简单的方法。例如,等宽(equal width)方法将属性的值域划分成具有相同宽度的区间,而区间的个数由用户指定。这种方法可能受离群点的影响而性能不佳,因此等频率(equal frequncy)或等深(equal depth)方法通常更为可取。等频率方法试图将相同数量的对象放进每个区间。作为非监督离散化的另一个例子,可以使用诸如K均值(见第8章)等聚类方法。最后,目测检查数据有时也可能是一种有效的方法。
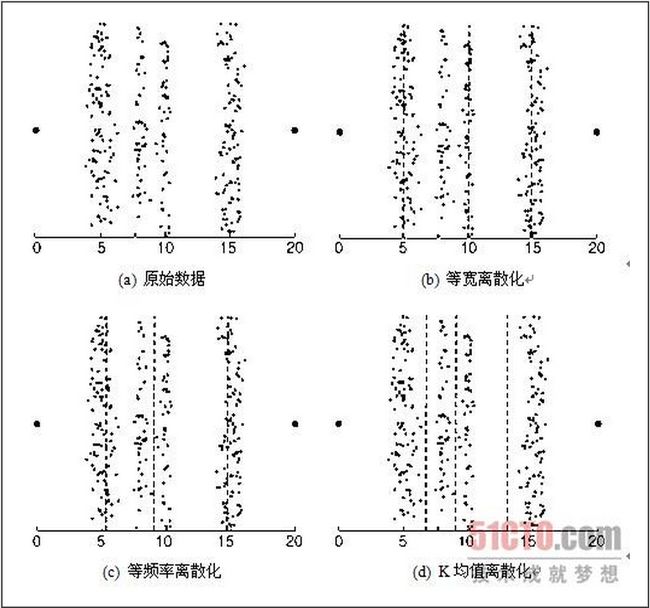
例2.12 离散化技术 本例解释如何对实际数据集使用这些技术。图2-13a显示了属于四个不同组的数据点,以及两个离群点--位于两边的大点。可以使用上述技术将这些数据点的x值离散化成四个分类值。(数据集中的点具有随机的y分量,可以更容易地看出每组有多少个点。)尽管目测检查该数据的方法效果很好,但不是自动的,因此我们主要讨论其他三种方法。使用等宽、等频率和K均值技术产生的分割点分别如图2-13b、图2-13c和图2-13d所示,图中分割点用虚线表示。如果我们用不同组的不同对象被指派到相同分类值的程度来度量离散化技术的性能,则K均值性能最好,其次是等频率,最后是等宽。
监督离散化 上面介绍的离散化方法通常比不离散化好,但是记住最终目的并使用附加的信息(类标号)常常能够产生更好的结果。这并不奇怪,因为未使用类标号知识所构造的区间常常包含混合的类标号。一种概念上的简单方法是以极大化区间纯度的方式确定分割点。然而,实践中这种方法可能需要人为确定区间的纯度和最小的区间大小。为了解决这一问题,一些基于统计学的方法用每个属性值来分隔区间,并通过合并类似于根据统计检验得出的相邻区间来创建较大的区间。基于熵的方法是最有前途的离散化方法之一,我们将给出一种简单的基于熵的方法。
首先,需要定义熵(entropy)。设k是不同的类标号数,mi是某划分的第i个区间中值的个数,而mij是区间i中类j的值的个数。第i个区间的熵ei由如下等式给出

其中pij=mij/mi, 是第i个区间中类j的概率(值的比例)。该划分的总熵e是每个区间的熵的加权平均,即
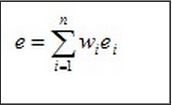
其中,m是值的个数,wi = mi/m是第i个区间的值的比例,而n 是区间个数。直观上,区间的熵是区间纯度的度量。如果一个区间只包含一个类的值(该区间非常纯),则其熵为0并且不影响总熵。如果一个区间中的值类出现的频率相等(该区间尽可能不纯),则其熵最大。
一种划分连续属性的简单方法是:开始,将初始值切分成两部分,让两个结果区间产生最小熵。该技术只需要把每个值看作可能的分割点即可,因为假定区间包含有序值的集合。然后,取一个区间,通常选取具有最大熵的区间,重复此分割过程,直到区间的个数达到用户指定的个数,或者满足终止条件。
例2.13 两个属性离散化 该方法用来独立地离散化图2-14所示的二维数据的属性x和y。在图2-14a所示的第一个离散化中,属性x和y被划分成三个区间。(虚线指示分割点。)在图2-14b所示的第二个离散化中,属性x和y被划分成五个区间。
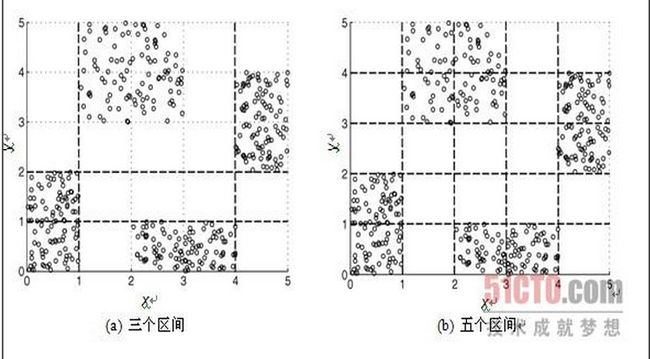
这个简单的例子解释了离散化的两个特点。首先,在二维中,点类是很好分开的,但在一维中,情况并非如此。一般而言,分别离散化每个属性通常只保证次最优的结果。其次,五个区间比三个好,但是,至少从熵的角度看,六个区间对离散化的改善不大。(没有给出六个区间的熵值和结果。)因而需要有一个终止标准,自动地发现划分的正确个数。
分类属性有时可能具有过多的值。如果分类属性是序数属性,则可以使用类似于处理连续属性的技术,以减少分类值的个数。然而,如果分类属性是标称的,就需要使用其他方法。考虑一所大学,它有许多系,因而系名属性可能具有数十个不同的值。在这种情况下,我们可以使用系之间联系的知识,将系合并成较大的组,如工程学、社会科学或生物科学。如果领域知识不能提供有用的指导,或者这样的方法会导致很差的分类性能,则需要使用更为经验性的方法,如仅当分组结果能提高分类准确率或达到某种其他数据挖掘目标时,才将值聚集到一起。
(7)变量变换
变量变换(属性交换)是指用于变量的所有值得变换。
书中介绍了两种重要的变量交换的方式:
这里介绍下第二个:
转自: http://www.jianshu.com/p/7958cb102095
数据挖掘过程中,不同变量数据单位不一,比如,我们想知道一个人身体健康状况,其身高是180cm,体重是80kg,视力是2.5,心跳是70/min,这些指标都是描述一个人身体状况的数据,这些单一不一的指标会对建模的准确度有一定影响。因此,在数据挖掘之前,我们要对数据做标准化处理。
另外,建模之后,我们产生了有价值的目标变量数据,但是这些数据都是标准化数据形式,跟实际业务问题的需求有一定偏差。如此,需要对数据做一定的变换,比如使其接近正态分布,这样从数据形式上可以对业务问题有更好的解释。
2,中心化
3, 极差 (变异量数、范围误差)标准化
4,小数定标规范化

度量数据的相似性和相异性:
补充点数学知识:
a^2 -b^2 = (a+b)(a-b) (平方差)
a^2 +b^2 +2ab = (a+b)^2 (和的平方)
a^2 +b^2 -2ab = (a-b)^2 (差的平方)
a^3 +b^3 = (a+b)(a^2 -ab +b^2) (立方和)
a^3 -b^3 = (a-b)(a^2 +ab +b^2) (立方差)
(a+b)^3 = a^3 +3(a^2)b +3a(b^2) +b^3 (和的立方)
(a-b)^3 = a^3 -3(a^2)b +3a(b^2) -b^3 (差的立方)
(a+b+c)^2 = a^2 +b^2 +c^2 +2ab +2bc + 2ca (三项和的平方)
计算公式编辑
二维空间的公式
0ρ = sqrt( (x1-x2)^2+(y1-y2)^2 ) |x| = √( x2 + y2 )
三维空间的公式
0ρ = √( (x1-x2)^2+(y1-y2)^2+(z1-z2)^2 ) |x| = √( x2 + y2 + z2 )
n维空间的公式
n维欧氏空间是一个点集,它的每个点 X 或向量 x 可以表示为 (x[1],x[2],…,x[n]) ,其中 x (i = 1,2,…,n) 是实数,称为 X 的第i个坐标。
两个点 A = (a[1],a[2],…,a[n]) 和 B = (b[1],b[2],…,b[n]) 之间的距离 ρ(A,B) 定义为下面的公式:
ρ(A,B) =√ [ ∑( a - b )^2 ] (i = 1,2,…,n)
向量 x = (x[1],x[2],…,x[n]) 的自然长度 |x| 定义为下面的公式:
|x| = √( x[1]^2 + x[2]^2 + … + x[n]^2 )
概述:
在诸如聚类、离群点分析和最近邻分类等数据挖掘应用中,我们需要评估对象之间相互比较的相似或不相似程度。例如,商店希望搜索顾客对象簇,得出具有类似特征(例如,类似的收入、居住区域和年龄等)的顾客组。这些信息可以用于销售。簇是数据对象的集合,使得同一个簇中的对象互相相似,而与其他簇中的对象相异。离群点分析也使用基于聚类的技术,把可能的离群点看做与其他对象高度相异的对象。对象的相似性可以用于最近邻分类,对给定的对象(例如,患者)基于它与模型中其他对象的相似性赋予一个类标号(比如说,诊断结论)。本节给出相似性和相异性度量。相似性和相异性都称邻近性(proximity)。相似性和相异性是有关联的。典型地,如果两个对象i和j不相似,则它们的相似性度量将返回0。相似性值越高,对象之间的相似性越大(典型地,值1指示完全相似,即对象是等同的)。相异性度量正好相反。如果对象相同(因而远非不相似),则它返回值0。相异性值越高,两个对象越相异。
定义:
两个对象之间的相似度的非正式定义是这两个对象相似程度的数值度量。因而,两个对象越相似,他们的相似度越高。通常,相似度是非负的。通常在0(不相似)和1(完全一样)之间取值。
变换:
数据对象之间的相异度 -> 距离(具有特定性质的相异度):
转自: http://www.niubua.com/?p=1319
1. 欧氏距离(Euclidean Distance)
欧式距离是高维空间中两点之间的距离,它计算简单、应用广泛,但是没有考虑变量之间的相关性,当体现单一特征的多个变量参与计算时会影响结果的准确性,同时它对向量中得每个分量的误差都同等对待,一定程度上放大了较大变量误差在距离测度中的作用。
两个n维向量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)间的欧氏距离定义为:D(A,B)=[(x11-x21)^2+(x12-x22)^2+…+(x1n-x2n)^2]^0.5
欧式距离的公式是
d=sqrt( ∑(xi1-xi2)^ ) 这里i=1,2..n
欧氏距离:(∑(Xi-Yi)2)1/2,即两项间的差是每个变量值差的平方和再平方根,目的是计算其间的整体距离即不相似性。
欧氏距离虽然很有用,但也有明显的缺点。它将样品的不同属性(即各指标或各变量)之间的差别等同看待,这一点有时不能满足实际要求。例如,在教育研究中, 经常遇到对人的分析和判别,个体的不同属性对于区分个体有着不同的重要性。因此,有时需要采用不同的距离函数。
欧氏距离看作信号的相似程度。 距离越近就越相似,就越容易相互干扰,误码率就越高。
2. 曼哈顿距离(Manhattan Distance)
曼哈顿距离也称为城市街区距离(City Block distance),想象在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。实际驾驶距离就是“曼哈顿距离”。
两个n维向量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)间的曼哈顿距离定义为:D(A,B)=|x11-x21|+|x12-x22|+…+|x1n-x2n|
两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼哈顿距离
以上两个距离都具有的数学性质是:
非负性:d(i,j)≥0 距离是一个非负的数值
同一性:d(i,i)= 0 对象到自身的距离为0
对称性:d(i,j)= d(j,i)距离是一个对称函数
三角不等式:d(i,j)≤d(i,k)+d(k,j)从对象i到对象j的直接距离不会大于途经的任何其他对象k的距离
3. 切比雪夫距离 (Chebyshev Distance )
数学上,切比雪夫距离(Chebyshev distance)或是L∞度量是向量空间中的一种度量,二个点之间的距离定义为其各座标数值差的最大值。以(x1,y1)和(x2,y2)二点为例,其切比雪夫距离为max(|x2-x1|,|y2-y1|)。切比雪夫距离得名自俄罗斯数学家切比雪夫。
切比雪夫距离也称为棋盘距离,国际象棋中,国王走一步能够移动到相邻的8个方格中的任意一个,那么国王从格子A(x1,y1)走到格子B(x2,y2)最少需要多少步?你会发现最少步数总是max{|x2-x1|,|y2-y1|}步。
两个n维向量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)间的切比雪夫距离定义为:D(A,B)=max{|x11-
x21|,|x12-x22|,…,|x1n-x2n|},该公式的另一种等价形式是:D(A,B)=[(x11-x21)^k+(x12-
x22)^k+…+(x1n-x2n)^k]^(1/k),其中k趋向于无穷大。
4. 闵氏距离(Minkowski Distance)
闵可夫斯基距离:

闵可夫斯基距离(Minkowski distance)是衡量数值点之间距离的一种非常常见的方法,假设数值点 P 和 Q 坐标如下:
那么,闵可夫斯基距离定义为:
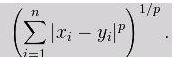
闵氏距离不是一种距离,而是一组距离的定义。
该距离最常用的 p 是 2 和 1, 前者是欧几里得距离(Euclidean distance),后者是曼哈顿距离(Manhattan distance)。假设在曼哈顿街区乘坐出租车从 P 点到 Q 点,白色表示高楼大厦,灰色表示街道:
绿色的斜线表示欧几里得距离,在现实中是不可能的。其他三条折线表示了曼哈顿距离,这三条折线的长度是相等的。
当 p 趋近于无穷大时,闵可夫斯基距离转化成切比雪夫距离(Chebyshev distance):
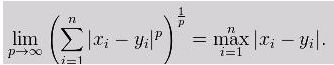
我们知道平面上到原点欧几里得距离(p = 2)为 1 的点所组成的形状是一个圆,当 p 取其他数值的时候呢?
注意,当 p < 1 时,闵可夫斯基距离不再符合三角形法则,举个例子:当 p < 1, (0,0) 到 (1,1) 的距离等于 (1 1)^{1/p} > 2, 而 (0,1) 到这两个点的距离都是 1。

闵可夫斯基距离比较直观,但是它与数据的分布无关,具有一定的局限性,如果 x 方向的幅值远远大于 y 方向的值,这个距离公式就会过度放大 x 维度的作用。所以,在计算距离之前,我们可能还需要对数据进行 z-transform 处理,即减去均值,除以标准差:

可以看到,上述处理开始体现数据的统计特性了。这种方法在假设数据各个维度不相关的情况下利用数据分布的特性计算出不同的距离。如果维度相互之间数据相关(例如:身高较高的信息很有可能会带来体重较重的信息,因为两者是有关联的),这时候就要用到马氏距离(Mahalanobis distance)了。
两个n维变量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)间的闵氏距离定义为:D(A,B)=[|x11-
x21|^p+|x12-x22|^p+…+|x1n-x2n|^p]^(1/p),其中p是一个可变参数。当p=1时为曼哈顿距离,当p=2时为欧氏距
离,当p→∞时为切比雪夫距离。
闵氏距离,包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点:(1)对各个分量的量纲(Scale)没有区别对待。(2)未考虑各个分量的分布(期望,方差等)可能是不同的。
5. 标准化欧氏距离(Standardized Euclidean Distance)
标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进,其基本思想是先将数据对象的各个分量都进行均值为μ、标准差为s的标准化,然后再计算欧式距离。
两个n维向量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)的标准化欧氏距离定义为:D(A,B)={[(x11-x21)/s1]^2+[(x12-x22)/s2]^2+…+[(x1n-x2n)/sn]^2}^0.5
6. 马氏距离(Mahalanobis Distance)
马氏距离由印度统计学家马哈拉诺斯(P.C.Mahalanobis)提出,表示数据的协方差距离,与欧式距离不同,它考虑了各指标之间相关性的干扰,而且不受各指标量纲的影响,但是它的缺点是夸大了变化微小的变量的作用。
设A、B是从均值向量为μ,协方差阵为∑的总体G中抽取的两个样本,A、B两点之间的马氏距离定义为:D(A,B)=[(A-B)T∑-1(A-B)]^0.5,A与总体G的马氏距离定义为D(A,G)=[(A-μ)T∑-1(A-μ)]^0.5。
当协方差矩阵∑是单位矩阵(各个样本向量之间独立同分布),则马氏公式就转化为欧氏距离;当协方差矩阵∑是对角阵时,则马氏距离就转化为标准化欧式距离;
7. 汉明距离(Hamming Distance)
在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。
例如:1011101 与 1001001 之间的汉明距离是 2;”toned”与”roses” 之间的汉明距离是3。
8. 皮尔逊相关系数(Pearson Correlation coefficient )
皮尔逊相关系数也称为简单相关系数,它是衡量随机变量X与Y相关程度的一种方法,相关系数的取值范围是[-1,1]。相关系数的绝对值越大,则表明X与Y相关度越高,负值表示负相关,正值表示正相关。
皮尔逊相关系数定义如下:r(X,Y)=Cov(X,Y)/[(D(X)^0.5)*(D(Y)^0.5)]=E((X-EX)*(Y-EY))/
[(D(X)^0.5)*(D(Y)^0.5)]=[(X1-X_bar)(Y1-Y_bar)+(X2-X_bar)(Y2-Y_bar)+…+
(Xn-X_bar)(Yn-Y_bar)]/{[(X1-X_bar)^2+(X2-X_bar)^2+…(Xn-X_bar)]*[(Y1-
Y_bar)^2+(Y2-Y_bar)^2+…(Yn-Y_bar)]}^0.5。
Pearson相关系数要求参与计算的变量为服从双变量正态分布的连续型数据,并且仅适用于线性相关的情况。另外,当极值对Pearson相关系数的影响非常大,因此在计算之前要首先进行极值处理。
9.斯皮尔曼秩相关系数(Spearman Rank Correlation)
与Pearson相关系数一样,它也可以反映两组变量联系的紧密程度,取值在-1到+1之间,计算方法上也完全相同,不同的是它建立在秩次的基础之上,对原始变量的分布和样本容量的大小不作要求,属于非参数统计方法,适用范围更广。
设R(R1,R2,…,Rn)表示X在(X1,X2,…,Xn)
中的秩,Q(Q1,Q2,…,Qn)表示Y在(Y1,Y2,…,Yn)中的秩,如果X和Y具有同步性,那么R和Q也会表现出同步性,反之依然,将其代入
Pearson相关系数,就得到秩之间的一致性,也就是Spearman相关系数。考虑到
R1+R2+…Rn=Q1+Q2+…+Qn=n(n+1)/2,R1^2+R2^2+…+Rn^2=Q1^2+Q2^2+…+Qn^2=n(n+1)
(2n+1)/6,Spearman相关系数可以定义为:r(X,Y)=1-6*[(R1-Q1)^2+(R2-Q2)^2+…(Rn-Qn)^2]
/[n(n^2-1)]
10.肯德尔秩相关系数(Kendall Rank Correlation )
Kendall在本质设想方面与Spearman是一样的,它从两个变量是否协同一致的角度出发检验两变量之间是否存在相关性。什么是协同?假设两
个变量X、Y有n对观察值(X1,Y1)(X2,Y2)…(Xn,Yn),如果(Xj-Xi)(Yj-Yi)>0(j>i),称
(Xi,Yi)与(Xj,Yj)满足协同性(concordant),或者说变化方向一致。否则,不满足协同性。
全部数据共有n(n-1)/2对,如果用Nc表示同向数对的数目,Nd表示反向数对的数目,则Nc+Nd=
n(n-1)/2,Kendall相关系数由两者的平均差定义:(Nc-Nd)/[n(n-1)/2]。Kendall相关系数的取值范围在-1到1之
间,当等于1时,表示两个随机变量拥有一致的等级相关性;当等于-1时,表示两个随机变量拥有完全相反的等级相关性;当等于0时,表示两个随机变量是相互
独立的。
11. 余弦相似度(Cosine Similarity)
几何中夹角余弦可用来衡量两个向量方向的差异,机器学习中用这一概念来衡量样本向量之间的差异。夹角余弦的取值范围为[-1,1]。夹角余弦越大表
示两个向量的夹角越小,夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1,当两个向量的方向完全相反夹角余弦取最小值-1。
两个n维样本向量A(x11,x12,…,x1n)和B(x21,x22,…,x2n)的夹角余弦定义为:cosθ=
(A·B)/(|A|*|B|)
=(x11*x21+x12*x22+…X1n*X2n)/[(x11^2+x12^2+…+x1n^2)^0.5*
(x21^2+x22^2+…+x2n^2)^0.5],夹角余弦经常应用于像文档这样的稀疏数据,它变量的长度无关,如向量(1,2)和(2,4)的夹
角余弦与向量(1,2)和(10,20)的相等。
欧氏距离是最常见的距离度量,而余弦相似度则是最常见的相似度度量,很多的距离度量和相似度度量都是基于这两者的变形和衍生,所以下面重点比较下两者在衡量个体差异时实现方式和应用环境上的区别。
借助三维坐标系来看下欧氏距离和余弦相似度的区别:
从图上可以看出距离度量衡量的是空间各点间的绝对距离,跟各个点所在的位置坐标(即个体特征维度的数值)直接相关;而余弦相似度衡量的是空间向量的夹角,更加的是体现在方向上的差异,而不是位置。如果保持A点的位置不变,B点朝原方向远离坐标轴原点,那么这个时候余弦相似度cosθ是保持不变的,因为夹角不变,而A、B两点的距离显然在发生改变,这就是欧氏距离和余弦相似度的不同之处。
根据欧氏距离和余弦相似度各自的计算方式和衡量特征,分别适用于不同的数据分析模型:欧氏距离能够体现个体数值特征的绝对差异,所以更多的用于需要从维度的数值大小中体现差异的分析,如使用用户行为指标分析用户价值的相似度或差异;而余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感,更多的用于使用用户对内容评分来区分用户兴趣的相似度和差异,同时修正了用户间可能存在的度量标准不统一的问题(因为余弦相似度对绝对数值不敏感)。
12.调整余弦相似度(Adjusted Cosine Similarity)
余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感。因此没法衡量每个维数值的差异,会导致这样一个情况:比如用户对内容评分,5分制,X
和Y两个用户对两个内容的评分分别为(1,2)和(4,5),使用余弦相似度得出的结果是0.98,两者极为相似,但从评分上看X似乎不喜欢这2个内容,
而Y比较喜欢,余弦相似度对数值的不敏感导致了结果的误差,需要修正这种不合理性。
调整余弦相似度,将所有维度上的数值都减去一个均值,比如X和Y的评分均值都是3,那么调整后为(-2,-1)和(1,2),再用余弦相似度计算,得到-0.8,相似度为负值并且差异不小,但显然更加符合现实。
13. 简单匹配系数(Simple Matching Coefficient,SMC)
设A、B是两个二元属性组成的对象,这两个对象的比较导致如下四个频率变量:f00:A取0并且B取0属性的个数;f01:A取0并且B取1属性的个数;f10:A取1并且B取0属性的个数;f11:A取1并且B取1属性的个数。
那么SMC就是两个对象A、B属性值匹配的属性个数与所有属性个数的比值,即SMC(A,B)=(f11+f00)/(f01+f10+f11+f00)
14. Jaccard系数(Jaccard Coefficient)
当数据对象的二元属性是非对称的时,例如用1表示商品被购买,用0表示商品未被购买。由于未被购买的商品数远远大于被购买的商品数,因此,如果用SMC计算数据对象的相似度,其结果必然是所有的数据对象都是相似的。
Jaccard系数可以处理仅包含非对称二元属性的对象,它是匹配属性的个数与不涉及0-0匹配的属性个数的比值,即J(A,B)=f11/(f01+f10+f11)。
15. 广义Jaccard系数(Extended Tanimoto Coefficient)
广义Jaccard系数又称为Tanimoto系数,常常用于文档数据,并在二元属性情况下规约为Jaccard系数。
该系数用EJ表示,定义如下:EJ(A,B)=(A·B)/(|A|*|A|+|B|*|B|-
A·B)=(x11*x21+x12*x22+…+x1n*x2n)/[(x11^2+x12^+…x1n^2)+(x21^2+x22^2+…+x2n^2)-(x11*x21+x12*x22+…+x1n*x2n)]

统计学常用概念:
1.频率:
在相同的条件下,进行了n次试验,在这n次试验中,事件A发生的次数m称为事件A发生的频数。
比值m/n称为事件A发生的频率,用文字表示定义为:每个对象出现的次数与总次数的比值是频率。
某个组的频数与样本容量的比值也叫做这个组的频率。有了频数(或频率)就可以知道数的分布情况。
2.众数:
众数(Mode)统计学名词,在统计分布上具有明显集中趋势点的数值,代表数据的一般水平(众数可以不存在或多于一个)。 修正定义:是一组数据中出现次数最多的数值,叫众数,有时众数在一组数中有好几个。用M表示。 理性理解:简单的说,就是一组数据中占比例最多的那个数。
3.位置度量:
平均数是统计中的一个重要概念。小学数学里所讲的平均数一般是指算术平均数,也就是一组数据的和除以这组数据的个数所得的商。在统计中算术平均数常用于表示统计对象的一般水平,它是描述数据集中位置的一个统计量。既可以用它来反映一组数据的一般情况、和平均水平,也可以用它进行不同组数据的比较,以看出组与组之间的差别。用平均数表示一组数据的情况,有直观、简明的特点,所以在日常生活中经常用到,如平均速度、平均身高、平均产量、平均成绩等等。
4.散布度量:
极差是指一组测量值内最大值与最小值之差,又称范围误差或全距,以R表示。它是标志值变动的最大范围,它是测定标志变动的最简单的指标。移动极差(Moving Range)是其中的一种。
极差没有充分利用数据的信息,但计算十分简单,仅适用样本容量较小(n<10)情况。
方差是衡量源数据和期望值相差的度量值。
数据预处理:
小知识复习:正太分布
(1)聚集
(2)抽样
(3)维归约
(4)特征子集选择
(5)特征创建
(6)离散化和二元化
转自: http://book.51cto.com/art/201011/235430.htm
有些数据挖掘算法,特别是某些分类算法,要求数据是分类属性形式。发现关联模式的算法要求数据是二元属性形式。这样,常常需要将连续属性变换成分类属性(离散化,discretization),并且连续和离散属性可能都需要变换成一个或多个二元属性(二元化,binarization)。此外,如果一个分类属性具有大量不同值(类别),或者某些值出现不频繁,则对于某些数据挖掘任务,通过合并某些值减少类别的数目可能是有益的。与特征选择一样,最佳的离散化和二元化方法是"对于用来分析数据的数据挖掘算法,产生最好结果"的方法。直接使用这种判别标准通常是不实际的。因此,离散化和二元化一般要满足这样一种判别标准,它与所考虑的数据挖掘任务的性能好坏直接相关。
- 二元化

这样的变换可能导致复杂化,如无意之中建立了转换后的属性之间的联系。例如,在表2-5中,属性x2和x3是相关的,因为good值使用这两个属性表示。此外,关联分析需要非对称的二元属性,其中只有属性的出现(值为1)才是重要的。因此,对于关联问题,需要为每一个分类值引入一个二元属性,如表2-6所示。如果结果属性的个数太多,则可以在二元化之前使用下面介绍的技术减少分类值的个数。转换见表

同样,对于关联问题,可能需要用两个非对称的二元属性替换单个二元属性。考虑记录人的性别(男、女)的二元属性,对于传统的关联规则算法,该信息需要转换成两个非对称的二元属性,其中一个仅当是男性时为1,而另一个仅当是女性时为1。(对于非对称的二元属性,由于其提供一个二进制位信息需要占用存储器的两个二进制位,因而在信息的表示上不太有效。)
- 连续属性离散化
通常,离散化应用于在分类或关联分析中使用到的属性上。一般来说,离散化的效果取决于所使用的算法,以及用到的其他属性。然而,属性离散化通常单独考虑。
连续属性变换成分类属性涉及两个子任务:决定需要多少个分类值,以及确定如何将连续属性值映射到这些分类值。在第一步中,将连续属性值排序后,通过指定n 1个分割点(split point)把它们分成n个区间。在颇为平凡的第二步中,将一个区间中的所有值映射到相同的分类值。因此,离散化问题就是决定选择多少个分割点和确定分割点位置的问题。结果可以用区间集合{(x0, x1], (x1, x2],..., (xn-1, xn)}表示,其中x0和xn可以分别为- 或+ ,或者用一系列不等式x0 < x≤x1,..., xn-1 < x < xn表示。
非监督离散化 用于分类的离散化方法之间的根本区别在于使用类信息(监督,supervised)还是不使用类信息(非监督,unsupervised)。如果不使用类信息,则常使用一些相对简单的方法。例如,等宽(equal width)方法将属性的值域划分成具有相同宽度的区间,而区间的个数由用户指定。这种方法可能受离群点的影响而性能不佳,因此等频率(equal frequncy)或等深(equal depth)方法通常更为可取。等频率方法试图将相同数量的对象放进每个区间。作为非监督离散化的另一个例子,可以使用诸如K均值(见第8章)等聚类方法。最后,目测检查数据有时也可能是一种有效的方法。
例2.12 离散化技术 本例解释如何对实际数据集使用这些技术。图2-13a显示了属于四个不同组的数据点,以及两个离群点--位于两边的大点。可以使用上述技术将这些数据点的x值离散化成四个分类值。(数据集中的点具有随机的y分量,可以更容易地看出每组有多少个点。)尽管目测检查该数据的方法效果很好,但不是自动的,因此我们主要讨论其他三种方法。使用等宽、等频率和K均值技术产生的分割点分别如图2-13b、图2-13c和图2-13d所示,图中分割点用虚线表示。如果我们用不同组的不同对象被指派到相同分类值的程度来度量离散化技术的性能,则K均值性能最好,其次是等频率,最后是等宽。

监督离散化 上面介绍的离散化方法通常比不离散化好,但是记住最终目的并使用附加的信息(类标号)常常能够产生更好的结果。这并不奇怪,因为未使用类标号知识所构造的区间常常包含混合的类标号。一种概念上的简单方法是以极大化区间纯度的方式确定分割点。然而,实践中这种方法可能需要人为确定区间的纯度和最小的区间大小。为了解决这一问题,一些基于统计学的方法用每个属性值来分隔区间,并通过合并类似于根据统计检验得出的相邻区间来创建较大的区间。基于熵的方法是最有前途的离散化方法之一,我们将给出一种简单的基于熵的方法。
首先,需要定义熵(entropy)。设k是不同的类标号数,mi是某划分的第i个区间中值的个数,而mij是区间i中类j的值的个数。第i个区间的熵ei由如下等式给出

其中pij=mij/mi, 是第i个区间中类j的概率(值的比例)。该划分的总熵e是每个区间的熵的加权平均,即
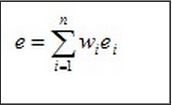
其中,m是值的个数,wi = mi/m是第i个区间的值的比例,而n 是区间个数。直观上,区间的熵是区间纯度的度量。如果一个区间只包含一个类的值(该区间非常纯),则其熵为0并且不影响总熵。如果一个区间中的值类出现的频率相等(该区间尽可能不纯),则其熵最大。
一种划分连续属性的简单方法是:开始,将初始值切分成两部分,让两个结果区间产生最小熵。该技术只需要把每个值看作可能的分割点即可,因为假定区间包含有序值的集合。然后,取一个区间,通常选取具有最大熵的区间,重复此分割过程,直到区间的个数达到用户指定的个数,或者满足终止条件。
例2.13 两个属性离散化 该方法用来独立地离散化图2-14所示的二维数据的属性x和y。在图2-14a所示的第一个离散化中,属性x和y被划分成三个区间。(虚线指示分割点。)在图2-14b所示的第二个离散化中,属性x和y被划分成五个区间。

这个简单的例子解释了离散化的两个特点。首先,在二维中,点类是很好分开的,但在一维中,情况并非如此。一般而言,分别离散化每个属性通常只保证次最优的结果。其次,五个区间比三个好,但是,至少从熵的角度看,六个区间对离散化的改善不大。(没有给出六个区间的熵值和结果。)因而需要有一个终止标准,自动地发现划分的正确个数。
- 具有过多值的分类属性
分类属性有时可能具有过多的值。如果分类属性是序数属性,则可以使用类似于处理连续属性的技术,以减少分类值的个数。然而,如果分类属性是标称的,就需要使用其他方法。考虑一所大学,它有许多系,因而系名属性可能具有数十个不同的值。在这种情况下,我们可以使用系之间联系的知识,将系合并成较大的组,如工程学、社会科学或生物科学。如果领域知识不能提供有用的指导,或者这样的方法会导致很差的分类性能,则需要使用更为经验性的方法,如仅当分组结果能提高分类准确率或达到某种其他数据挖掘目标时,才将值聚集到一起。
(7)变量变换
变量变换(属性交换)是指用于变量的所有值得变换。
书中介绍了两种重要的变量交换的方式:
- 简单函数
- 规范化和标准化
这里介绍下第二个:
转自: http://www.jianshu.com/p/7958cb102095
数据挖掘过程中,不同变量数据单位不一,比如,我们想知道一个人身体健康状况,其身高是180cm,体重是80kg,视力是2.5,心跳是70/min,这些指标都是描述一个人身体状况的数据,这些单一不一的指标会对建模的准确度有一定影响。因此,在数据挖掘之前,我们要对数据做标准化处理。
另外,建模之后,我们产生了有价值的目标变量数据,但是这些数据都是标准化数据形式,跟实际业务问题的需求有一定偏差。如此,需要对数据做一定的变换,比如使其接近正态分布,这样从数据形式上可以对业务问题有更好的解释。
- 数据标准化
2,中心化
3, 极差 (变异量数、范围误差)标准化
4,小数定标规范化
度量数据的相似性和相异性:
补充点数学知识:
- 常用平方公式:
a^2 -b^2 = (a+b)(a-b) (平方差)
a^2 +b^2 +2ab = (a+b)^2 (和的平方)
a^2 +b^2 -2ab = (a-b)^2 (差的平方)
a^3 +b^3 = (a+b)(a^2 -ab +b^2) (立方和)
a^3 -b^3 = (a-b)(a^2 +ab +b^2) (立方差)
(a+b)^3 = a^3 +3(a^2)b +3a(b^2) +b^3 (和的立方)
(a-b)^3 = a^3 -3(a^2)b +3a(b^2) -b^3 (差的立方)
(a+b+c)^2 = a^2 +b^2 +c^2 +2ab +2bc + 2ca (三项和的平方)
- 欧几里得度量
计算公式编辑
二维空间的公式
0ρ = sqrt( (x1-x2)^2+(y1-y2)^2 ) |x| = √( x2 + y2 )
三维空间的公式
0ρ = √( (x1-x2)^2+(y1-y2)^2+(z1-z2)^2 ) |x| = √( x2 + y2 + z2 )
n维空间的公式
n维欧氏空间是一个点集,它的每个点 X 或向量 x 可以表示为 (x[1],x[2],…,x[n]) ,其中 x (i = 1,2,…,n) 是实数,称为 X 的第i个坐标。
两个点 A = (a[1],a[2],…,a[n]) 和 B = (b[1],b[2],…,b[n]) 之间的距离 ρ(A,B) 定义为下面的公式:
ρ(A,B) =√ [ ∑( a - b )^2 ] (i = 1,2,…,n)
向量 x = (x[1],x[2],…,x[n]) 的自然长度 |x| 定义为下面的公式:
|x| = √( x[1]^2 + x[2]^2 + … + x[n]^2 )
概述:
在诸如聚类、离群点分析和最近邻分类等数据挖掘应用中,我们需要评估对象之间相互比较的相似或不相似程度。例如,商店希望搜索顾客对象簇,得出具有类似特征(例如,类似的收入、居住区域和年龄等)的顾客组。这些信息可以用于销售。簇是数据对象的集合,使得同一个簇中的对象互相相似,而与其他簇中的对象相异。离群点分析也使用基于聚类的技术,把可能的离群点看做与其他对象高度相异的对象。对象的相似性可以用于最近邻分类,对给定的对象(例如,患者)基于它与模型中其他对象的相似性赋予一个类标号(比如说,诊断结论)。本节给出相似性和相异性度量。相似性和相异性都称邻近性(proximity)。相似性和相异性是有关联的。典型地,如果两个对象i和j不相似,则它们的相似性度量将返回0。相似性值越高,对象之间的相似性越大(典型地,值1指示完全相似,即对象是等同的)。相异性度量正好相反。如果对象相同(因而远非不相似),则它返回值0。相异性值越高,两个对象越相异。
定义:
- 相似度:
两个对象之间的相似度的非正式定义是这两个对象相似程度的数值度量。因而,两个对象越相似,他们的相似度越高。通常,相似度是非负的。通常在0(不相似)和1(完全一样)之间取值。
- 相异度:
变换:
- 相似度 -> 相异度
- 把邻近度换到一个特定区间
数据对象之间的相异度 -> 距离(具有特定性质的相异度):
转自: http://www.niubua.com/?p=1319
1. 欧氏距离(Euclidean Distance)
欧式距离是高维空间中两点之间的距离,它计算简单、应用广泛,但是没有考虑变量之间的相关性,当体现单一特征的多个变量参与计算时会影响结果的准确性,同时它对向量中得每个分量的误差都同等对待,一定程度上放大了较大变量误差在距离测度中的作用。
两个n维向量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)间的欧氏距离定义为:D(A,B)=[(x11-x21)^2+(x12-x22)^2+…+(x1n-x2n)^2]^0.5
欧式距离的公式是
d=sqrt( ∑(xi1-xi2)^ ) 这里i=1,2..n
欧氏距离:(∑(Xi-Yi)2)1/2,即两项间的差是每个变量值差的平方和再平方根,目的是计算其间的整体距离即不相似性。
欧氏距离虽然很有用,但也有明显的缺点。它将样品的不同属性(即各指标或各变量)之间的差别等同看待,这一点有时不能满足实际要求。例如,在教育研究中, 经常遇到对人的分析和判别,个体的不同属性对于区分个体有着不同的重要性。因此,有时需要采用不同的距离函数。
欧氏距离看作信号的相似程度。 距离越近就越相似,就越容易相互干扰,误码率就越高。
2. 曼哈顿距离(Manhattan Distance)
曼哈顿距离也称为城市街区距离(City Block distance),想象在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。实际驾驶距离就是“曼哈顿距离”。
两个n维向量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)间的曼哈顿距离定义为:D(A,B)=|x11-x21|+|x12-x22|+…+|x1n-x2n|
两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼哈顿距离
以上两个距离都具有的数学性质是:
非负性:d(i,j)≥0 距离是一个非负的数值
同一性:d(i,i)= 0 对象到自身的距离为0
对称性:d(i,j)= d(j,i)距离是一个对称函数
三角不等式:d(i,j)≤d(i,k)+d(k,j)从对象i到对象j的直接距离不会大于途经的任何其他对象k的距离
3. 切比雪夫距离 (Chebyshev Distance )
数学上,切比雪夫距离(Chebyshev distance)或是L∞度量是向量空间中的一种度量,二个点之间的距离定义为其各座标数值差的最大值。以(x1,y1)和(x2,y2)二点为例,其切比雪夫距离为max(|x2-x1|,|y2-y1|)。切比雪夫距离得名自俄罗斯数学家切比雪夫。
切比雪夫距离也称为棋盘距离,国际象棋中,国王走一步能够移动到相邻的8个方格中的任意一个,那么国王从格子A(x1,y1)走到格子B(x2,y2)最少需要多少步?你会发现最少步数总是max{|x2-x1|,|y2-y1|}步。
两个n维向量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)间的切比雪夫距离定义为:D(A,B)=max{|x11-
x21|,|x12-x22|,…,|x1n-x2n|},该公式的另一种等价形式是:D(A,B)=[(x11-x21)^k+(x12-
x22)^k+…+(x1n-x2n)^k]^(1/k),其中k趋向于无穷大。
4. 闵氏距离(Minkowski Distance)
闵可夫斯基距离:
闵可夫斯基距离(Minkowski distance)是衡量数值点之间距离的一种非常常见的方法,假设数值点 P 和 Q 坐标如下:
那么,闵可夫斯基距离定义为:
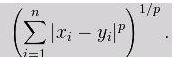
闵氏距离不是一种距离,而是一组距离的定义。
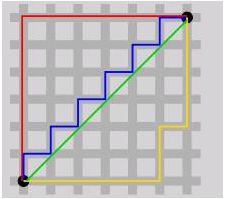
该距离最常用的 p 是 2 和 1, 前者是欧几里得距离(Euclidean distance),后者是曼哈顿距离(Manhattan distance)。假设在曼哈顿街区乘坐出租车从 P 点到 Q 点,白色表示高楼大厦,灰色表示街道:

绿色的斜线表示欧几里得距离,在现实中是不可能的。其他三条折线表示了曼哈顿距离,这三条折线的长度是相等的。
当 p 趋近于无穷大时,闵可夫斯基距离转化成切比雪夫距离(Chebyshev distance):
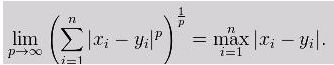
我们知道平面上到原点欧几里得距离(p = 2)为 1 的点所组成的形状是一个圆,当 p 取其他数值的时候呢?
注意,当 p < 1 时,闵可夫斯基距离不再符合三角形法则,举个例子:当 p < 1, (0,0) 到 (1,1) 的距离等于 (1 1)^{1/p} > 2, 而 (0,1) 到这两个点的距离都是 1。

闵可夫斯基距离比较直观,但是它与数据的分布无关,具有一定的局限性,如果 x 方向的幅值远远大于 y 方向的值,这个距离公式就会过度放大 x 维度的作用。所以,在计算距离之前,我们可能还需要对数据进行 z-transform 处理,即减去均值,除以标准差:

可以看到,上述处理开始体现数据的统计特性了。这种方法在假设数据各个维度不相关的情况下利用数据分布的特性计算出不同的距离。如果维度相互之间数据相关(例如:身高较高的信息很有可能会带来体重较重的信息,因为两者是有关联的),这时候就要用到马氏距离(Mahalanobis distance)了。
两个n维变量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)间的闵氏距离定义为:D(A,B)=[|x11-
x21|^p+|x12-x22|^p+…+|x1n-x2n|^p]^(1/p),其中p是一个可变参数。当p=1时为曼哈顿距离,当p=2时为欧氏距
离,当p→∞时为切比雪夫距离。
闵氏距离,包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点:(1)对各个分量的量纲(Scale)没有区别对待。(2)未考虑各个分量的分布(期望,方差等)可能是不同的。
5. 标准化欧氏距离(Standardized Euclidean Distance)
标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进,其基本思想是先将数据对象的各个分量都进行均值为μ、标准差为s的标准化,然后再计算欧式距离。
两个n维向量A(x11,x12,…,x1n)与B(x21,x22,…,x2n)的标准化欧氏距离定义为:D(A,B)={[(x11-x21)/s1]^2+[(x12-x22)/s2]^2+…+[(x1n-x2n)/sn]^2}^0.5
6. 马氏距离(Mahalanobis Distance)
马氏距离由印度统计学家马哈拉诺斯(P.C.Mahalanobis)提出,表示数据的协方差距离,与欧式距离不同,它考虑了各指标之间相关性的干扰,而且不受各指标量纲的影响,但是它的缺点是夸大了变化微小的变量的作用。
设A、B是从均值向量为μ,协方差阵为∑的总体G中抽取的两个样本,A、B两点之间的马氏距离定义为:D(A,B)=[(A-B)T∑-1(A-B)]^0.5,A与总体G的马氏距离定义为D(A,G)=[(A-μ)T∑-1(A-μ)]^0.5。
当协方差矩阵∑是单位矩阵(各个样本向量之间独立同分布),则马氏公式就转化为欧氏距离;当协方差矩阵∑是对角阵时,则马氏距离就转化为标准化欧式距离;
7. 汉明距离(Hamming Distance)
在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。
例如:1011101 与 1001001 之间的汉明距离是 2;”toned”与”roses” 之间的汉明距离是3。
8. 皮尔逊相关系数(Pearson Correlation coefficient )
皮尔逊相关系数也称为简单相关系数,它是衡量随机变量X与Y相关程度的一种方法,相关系数的取值范围是[-1,1]。相关系数的绝对值越大,则表明X与Y相关度越高,负值表示负相关,正值表示正相关。
皮尔逊相关系数定义如下:r(X,Y)=Cov(X,Y)/[(D(X)^0.5)*(D(Y)^0.5)]=E((X-EX)*(Y-EY))/
[(D(X)^0.5)*(D(Y)^0.5)]=[(X1-X_bar)(Y1-Y_bar)+(X2-X_bar)(Y2-Y_bar)+…+
(Xn-X_bar)(Yn-Y_bar)]/{[(X1-X_bar)^2+(X2-X_bar)^2+…(Xn-X_bar)]*[(Y1-
Y_bar)^2+(Y2-Y_bar)^2+…(Yn-Y_bar)]}^0.5。
Pearson相关系数要求参与计算的变量为服从双变量正态分布的连续型数据,并且仅适用于线性相关的情况。另外,当极值对Pearson相关系数的影响非常大,因此在计算之前要首先进行极值处理。
9.斯皮尔曼秩相关系数(Spearman Rank Correlation)
与Pearson相关系数一样,它也可以反映两组变量联系的紧密程度,取值在-1到+1之间,计算方法上也完全相同,不同的是它建立在秩次的基础之上,对原始变量的分布和样本容量的大小不作要求,属于非参数统计方法,适用范围更广。
设R(R1,R2,…,Rn)表示X在(X1,X2,…,Xn)
中的秩,Q(Q1,Q2,…,Qn)表示Y在(Y1,Y2,…,Yn)中的秩,如果X和Y具有同步性,那么R和Q也会表现出同步性,反之依然,将其代入
Pearson相关系数,就得到秩之间的一致性,也就是Spearman相关系数。考虑到
R1+R2+…Rn=Q1+Q2+…+Qn=n(n+1)/2,R1^2+R2^2+…+Rn^2=Q1^2+Q2^2+…+Qn^2=n(n+1)
(2n+1)/6,Spearman相关系数可以定义为:r(X,Y)=1-6*[(R1-Q1)^2+(R2-Q2)^2+…(Rn-Qn)^2]
/[n(n^2-1)]
10.肯德尔秩相关系数(Kendall Rank Correlation )
Kendall在本质设想方面与Spearman是一样的,它从两个变量是否协同一致的角度出发检验两变量之间是否存在相关性。什么是协同?假设两
个变量X、Y有n对观察值(X1,Y1)(X2,Y2)…(Xn,Yn),如果(Xj-Xi)(Yj-Yi)>0(j>i),称
(Xi,Yi)与(Xj,Yj)满足协同性(concordant),或者说变化方向一致。否则,不满足协同性。
全部数据共有n(n-1)/2对,如果用Nc表示同向数对的数目,Nd表示反向数对的数目,则Nc+Nd=
n(n-1)/2,Kendall相关系数由两者的平均差定义:(Nc-Nd)/[n(n-1)/2]。Kendall相关系数的取值范围在-1到1之
间,当等于1时,表示两个随机变量拥有一致的等级相关性;当等于-1时,表示两个随机变量拥有完全相反的等级相关性;当等于0时,表示两个随机变量是相互
独立的。
11. 余弦相似度(Cosine Similarity)
几何中夹角余弦可用来衡量两个向量方向的差异,机器学习中用这一概念来衡量样本向量之间的差异。夹角余弦的取值范围为[-1,1]。夹角余弦越大表
示两个向量的夹角越小,夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1,当两个向量的方向完全相反夹角余弦取最小值-1。
两个n维样本向量A(x11,x12,…,x1n)和B(x21,x22,…,x2n)的夹角余弦定义为:cosθ=
(A·B)/(|A|*|B|)
=(x11*x21+x12*x22+…X1n*X2n)/[(x11^2+x12^2+…+x1n^2)^0.5*
(x21^2+x22^2+…+x2n^2)^0.5],夹角余弦经常应用于像文档这样的稀疏数据,它变量的长度无关,如向量(1,2)和(2,4)的夹
角余弦与向量(1,2)和(10,20)的相等。
欧氏距离是最常见的距离度量,而余弦相似度则是最常见的相似度度量,很多的距离度量和相似度度量都是基于这两者的变形和衍生,所以下面重点比较下两者在衡量个体差异时实现方式和应用环境上的区别。
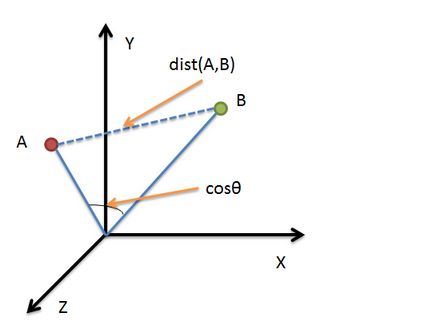
借助三维坐标系来看下欧氏距离和余弦相似度的区别:

从图上可以看出距离度量衡量的是空间各点间的绝对距离,跟各个点所在的位置坐标(即个体特征维度的数值)直接相关;而余弦相似度衡量的是空间向量的夹角,更加的是体现在方向上的差异,而不是位置。如果保持A点的位置不变,B点朝原方向远离坐标轴原点,那么这个时候余弦相似度cosθ是保持不变的,因为夹角不变,而A、B两点的距离显然在发生改变,这就是欧氏距离和余弦相似度的不同之处。
根据欧氏距离和余弦相似度各自的计算方式和衡量特征,分别适用于不同的数据分析模型:欧氏距离能够体现个体数值特征的绝对差异,所以更多的用于需要从维度的数值大小中体现差异的分析,如使用用户行为指标分析用户价值的相似度或差异;而余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感,更多的用于使用用户对内容评分来区分用户兴趣的相似度和差异,同时修正了用户间可能存在的度量标准不统一的问题(因为余弦相似度对绝对数值不敏感)。
12.调整余弦相似度(Adjusted Cosine Similarity)
余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感。因此没法衡量每个维数值的差异,会导致这样一个情况:比如用户对内容评分,5分制,X
和Y两个用户对两个内容的评分分别为(1,2)和(4,5),使用余弦相似度得出的结果是0.98,两者极为相似,但从评分上看X似乎不喜欢这2个内容,
而Y比较喜欢,余弦相似度对数值的不敏感导致了结果的误差,需要修正这种不合理性。
调整余弦相似度,将所有维度上的数值都减去一个均值,比如X和Y的评分均值都是3,那么调整后为(-2,-1)和(1,2),再用余弦相似度计算,得到-0.8,相似度为负值并且差异不小,但显然更加符合现实。
13. 简单匹配系数(Simple Matching Coefficient,SMC)
设A、B是两个二元属性组成的对象,这两个对象的比较导致如下四个频率变量:f00:A取0并且B取0属性的个数;f01:A取0并且B取1属性的个数;f10:A取1并且B取0属性的个数;f11:A取1并且B取1属性的个数。
那么SMC就是两个对象A、B属性值匹配的属性个数与所有属性个数的比值,即SMC(A,B)=(f11+f00)/(f01+f10+f11+f00)
14. Jaccard系数(Jaccard Coefficient)
当数据对象的二元属性是非对称的时,例如用1表示商品被购买,用0表示商品未被购买。由于未被购买的商品数远远大于被购买的商品数,因此,如果用SMC计算数据对象的相似度,其结果必然是所有的数据对象都是相似的。
Jaccard系数可以处理仅包含非对称二元属性的对象,它是匹配属性的个数与不涉及0-0匹配的属性个数的比值,即J(A,B)=f11/(f01+f10+f11)。
15. 广义Jaccard系数(Extended Tanimoto Coefficient)
广义Jaccard系数又称为Tanimoto系数,常常用于文档数据,并在二元属性情况下规约为Jaccard系数。
该系数用EJ表示,定义如下:EJ(A,B)=(A·B)/(|A|*|A|+|B|*|B|-
A·B)=(x11*x21+x12*x22+…+x1n*x2n)/[(x11^2+x12^+…x1n^2)+(x21^2+x22^2+…+x2n^2)-(x11*x21+x12*x22+…+x1n*x2n)]
统计学常用概念:
1.频率:
在相同的条件下,进行了n次试验,在这n次试验中,事件A发生的次数m称为事件A发生的频数。
比值m/n称为事件A发生的频率,用文字表示定义为:每个对象出现的次数与总次数的比值是频率。
某个组的频数与样本容量的比值也叫做这个组的频率。有了频数(或频率)就可以知道数的分布情况。
2.众数:
众数(Mode)统计学名词,在统计分布上具有明显集中趋势点的数值,代表数据的一般水平(众数可以不存在或多于一个)。 修正定义:是一组数据中出现次数最多的数值,叫众数,有时众数在一组数中有好几个。用M表示。 理性理解:简单的说,就是一组数据中占比例最多的那个数。
3.位置度量:
- 平均数:
平均数是统计中的一个重要概念。小学数学里所讲的平均数一般是指算术平均数,也就是一组数据的和除以这组数据的个数所得的商。在统计中算术平均数常用于表示统计对象的一般水平,它是描述数据集中位置的一个统计量。既可以用它来反映一组数据的一般情况、和平均水平,也可以用它进行不同组数据的比较,以看出组与组之间的差别。用平均数表示一组数据的情况,有直观、简明的特点,所以在日常生活中经常用到,如平均速度、平均身高、平均产量、平均成绩等等。
- 中位数:
4.散布度量:
- 极差:
极差是指一组测量值内最大值与最小值之差,又称范围误差或全距,以R表示。它是标志值变动的最大范围,它是测定标志变动的最简单的指标。移动极差(Moving Range)是其中的一种。
极差没有充分利用数据的信息,但计算十分简单,仅适用样本容量较小(n<10)情况。
- 方差:
方差是衡量源数据和期望值相差的度量值。