Honeycomb (Gym-102028F)
Problem Description
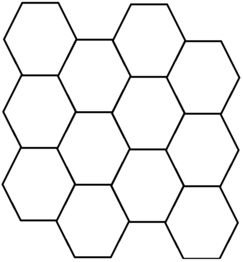
A honeycomb is a mass wax cells built by honey bees, which can be described as a regular tiling of the Euclidean plane, in which three hexagons meet at each internal vertex. The internal angle of a hexagon is 120 degrees, so three hexagons at a point make a full 360 degrees. The following figure shows a complete honeycomb with 33 rows and 4 columns.
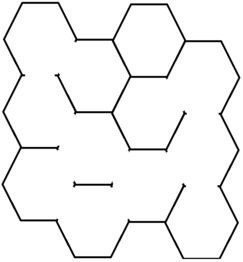
Here we guarantee that the first cell in the second column always locates in the bottom right side of the first cell in the first column, as shown above. A general honeycomb may, on the basis of a complete honeycomb, lose some walls between adjacent cells, but the honeycomb is still in a closed form. A possible case looks like the figure below.
Hamilton is a brave bee living in a general honeycomb. Now he wants to move from a starting point to a specified destination. The image below gives a feasible path in a 3×4 honeycomb from the 1-st cell in the 2-nd column to the 1-st cell in the 4-th column.
Please help him find the minimum number of cells that a feasible path has to pass through (including the starting point and the destination) from the specified starting point to the destination.
Input
The input contains several test cases, and the first line contains a positive integer T indicating the number of test cases which is up to 104.
For each test case, the first line contains two integers rr and cc indicating the number of rows and the number of columns of the honeycomb, where 2≤r,c≤103.
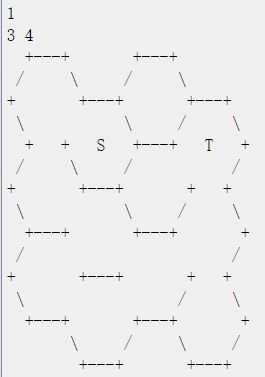
The following (4r+3) lines describe the whole given honeycomb, where each line contains at most (6c+3) characters. Odd lines contain grid vertices represented as plus signs ("+") and zero or more horizontal edges, while even lines contain two or more diagonal edges. Specifically, a cell is described as 66 vertices and at most 66 edges. Its upper boundary or lower boundary is represented as three consecutive minus signs ("-"). Each one of its diagonal edges, if exists, is a single forward slash ("/") or a single backslash ("\") character. All edge characters will be placed exactly between the corresponding vertices. At the center of the starting cell (resp. the destination), a capital "S" (resp. a capital "T") as a special character is used to indicate the special cell. All other characters will be space characters. Note that if any input line could contain trailing whitespace, that whitespace will be omitted.
We guarantee that all outermost wall exist so that the given honeycomb is closed, and exactly one "S" and one "T" appear in the given honeycomb. Besides, the sum of r⋅c in all test cases is up to 2×106.
Output
For each test case, output a line containing the minimum number of cells that Hamilton has to visit moving from the starting cell ("S") to the destination ("T"), including the starting cell and the destination. If no feasible path exists, output -1 instead.
Examples
Input
Output
7
题意:t 组样例,每组给出若干由字符构成的六边形单元格,总共 n 行 m 列,现在在某两个单元格中有一个 S 一个 T 分别代表起点和重点,问从 S 到 T 的最短路径
思路:
如果图不是由字符给出的,那么是一个 Dijkstra 裸题,题目的难点在于如何建图
从 1 开始,从左到右从上到下,依次分配单元格序号,共有 n*m 个单元格,然后将图读入后数格子找规律连边建图即可,具体看程序
Source Program
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include