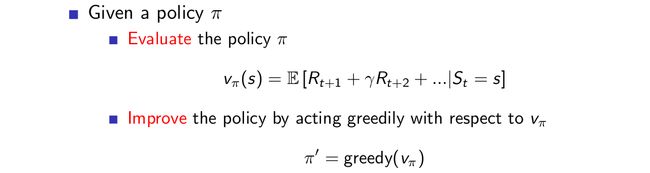David Silver强化学习课程笔记（三）

第三课：动态规划

        课程标题本来是“Planning by Dynamic Programming”，应该翻译为”利用动态规划方法进行规划“，但是感觉有点长，所以就使用”动态规划“作为标题，大家理解就好......

        先说下这节课讲的主要内容，主要有：策略估计、策略迭代、值迭代、动态规划扩展、收缩映射定理。其中策略估计主要介绍如何利用迭代方法对策略的值函数进行估计，也即我们在第一课中讨论的问题；策略迭代与值迭代则是在策略估计的基础上，引入策略改进，从而达到控制的目的，二者的主要区别是策略迭代基于贝尔曼期望方程和贪婪法，而值迭代则是基于贝尔曼最优方程；动态规划扩展介绍了几种改进方法；最后的收缩映射证明了策略迭代与值迭代都将收敛到最优策略。

       1.动态规划简介

        什么是动态规划（DP）？课程中给出了这样的释义：Dynamic means the sequential or temporal component to the problem; Programming means optimising a "program", i.e. a policy。就是说”动态“指的是该问题的时间序贯部分，”规划“指的是去优化一个计划，换句话说，优化一个策略。

        动态规划通常分为三步：a）将问题分解为子问题；b）求解子问题；c）合并子问题的解。

        是不是所有问题都能用动态规划求解呢？不是的，动态规划方法需要我们的问题包含以下两个性质：

        a）最优子结构：保证问题能够使用最优性准则，从而问题的最优解可以分解为子问题最优解；

        b）重叠子问题：子问题重复出现多次，因而我们可以缓存并重用子问题的解。

        恰巧，MDP满足上面两个性质，贝尔曼方程给出了问题的迭代分解，值函数保存和重用问题的解。因此，我们可以利用动态规划方法来求解MDP规划问题，此时假定MDP的模型是已知的，DP方法既可用于预测，也可用于控制：

      

       2.迭代策略估计

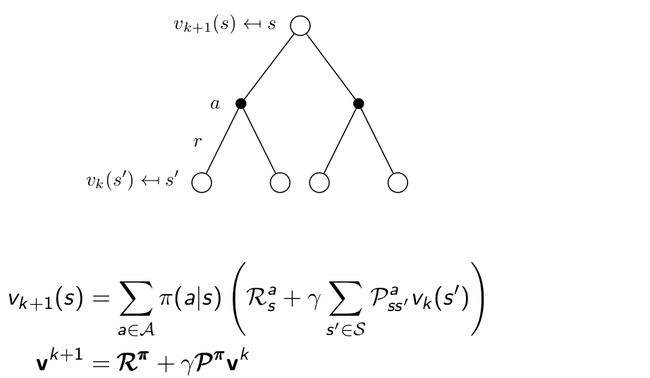
        策略估计指的是对于某一个给定的策略，估计其值函数。一般来说，我们通过迭代使用贝尔曼期望方程backup来进行求解（这里说到的backup也即第二章中提到的推演，从backup的字面意思可以较好地理解这一含义）。

        首先我们讨论同步backup，在后面”几种动态规划的改进方法“中讨论如何使用异步backup。同步backup步骤如下：

      

        其示意图如下：

      

        也即，我们利用上一个时间步的值函数来更新当前时间步的值函数，迭代应用这一更新公式，从而收敛至策略对应的真实值函数。

       3.策略迭代

        上一个小节中我们讨论了如何使用贝尔曼期望方程进行策略估计，并没有对策略进行改进，也就是说，策略还是那个策略，而如果我们要解决控制问题，而不是预测问题的话，对策略进行改进是必要的，我们总是希望去找到某个问题的最优策略。如何改进策略？可以通过对于old policy的值函数采用贪婪法即可得到改进的策略：

      

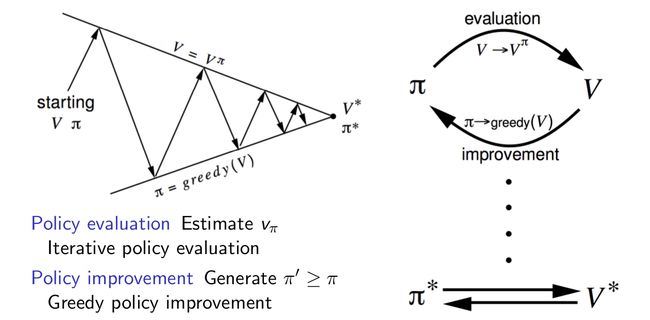
        对于较小的格子世界问题，上面这两步操作可以直接得到最优策略，但是通常来说，我们需要更多的估计/改进迭代（也即我们给出一个初始策略，估计其值函数至接近真实值，然后利用贪婪方法得到改进的策略，接着对改进后的策略进行估计......）。尽管如此，我们的策略迭代方法总能收敛到最优策略，下面用示意图来表示策略迭代的过程：

      

        我们可以对贪婪法总能对策略做出改进这一现象进行证明：

      

        如果整个策略迭代完成，则上述证明中的等号成立，此时贝尔曼最优方程得以满足，也即最终得到的策略是最优策略，其值函数是最优值函数。

        策略迭代在每一个迭代步总是先对策略进行值函数估计，直至收敛，那我们能否在策略估计还未收敛时就进行策略改进呢？比如说引入epsilon收敛 ，比如简单地在对策略估计迭代k次之后就进行策略改进，甚至，k=1就进行策略改进又会怎么样呢？下面我们将会讲到，k=1的情形就是值迭代方法。

        此外，我们可以将策略迭代方法拓展到一般化的策略迭代方法：首先估计策略的值函数，然后使用任意策略改进算法对策略进行改进，例如这里的greedy方法，迭代执行这两步，直至收敛即可。

       4.值迭代

        说到值迭代，先聊一聊最优性原理总是好的，毕竟本文开头就聊到了策略迭代是基于贝尔曼期望方程和贪婪法的，而值迭代则是基于贝尔曼最优方程的，所以我们先看一下最优性原理：

      

        通俗地说，最优性原理可以理解为：对于某一个最优决策序列而言，不论初始状态和初始决策如何，对于前面决策所造成的某一状态而言，其后各阶段的决策序列必须构成最优策略。对于值函数使用最优性原理：

      

        我们可以看一下值迭代的步骤：

      

        与策略迭代一样，值迭代最终也同样收敛到最优值函数，不过，与策略迭代不一样的是，值迭代没有显式的策略，它通过贝尔曼最优方程，隐式地实现了策略改进这一步。值得注意的是，中间过程中的值函数可能并不对应于任何策略。我们通过backup图来对值迭代进行理解：

        与贝尔曼期望方程相比，贝尔曼最优方程将期望操作变为最大操作，也即隐式地实现了策略改进这一步，不过是固定为greedy的，而不是其他策略改进方法，我们通过greedy得到的策略通常为确定性策略。

        5.策略估计、策略迭代、值迭代总结

      

        关于复杂度的计算说明一下，比如对于贝尔曼最优方程更新状态值函数，首先对于某一个状态s对应的值，我们需要将转移之后的状态s'乘以转移矩阵求和，计算复杂度为n，其次对于m个动作求最大，复杂度为m，最后，所有n个状态都要更新，因此总的计算复杂度为m*n^2；而对于动作值函数的更新，为(s',a')->(s,a)，也即m*n->m*n，所以总计算复杂度为(m^2)*(n^2)。

       6.动态规划扩展

        首先介绍异步动态规划，前面我们介绍的方法都是用的同步动态规划，也就是说，所有的状态一起进行backup，而异步动态规划则是将所有states独立进行backup，并且是以任意顺序。异步动态规划可以减少计算量，不过如果想要收敛，则需要满足一个条件：所有状态都需要能够持续被选择，或者说，在任一时刻，任何状态都有可能被选中。异步动态规划主要有三个简单的idea：

        1）In-place dynamic programming;

        2）Prioritised sweeping;

        3）Real-time dynamic programming.

        直接放图啦：

      

      

      

        对于DP而言，它的推演是整个树状散开的，我们称这种方法为Full-Width Backup方法。在这种方法中，对于每一次backup来说，所有的后继状态和动作都要被考虑在内，并且需要已知MDP的转移矩阵与奖励函数，因此DP将面临维数灾难问题。所以我们就有了Sample Backup，这种方法将在后面进行介绍，其主要思想是利用样本进行backup，优点有a）Model-free；b）避免了维数灾难问题；c）backup的代价与状态数n无关。如下图所示：

      

        最后介绍一种DP的扩展，叫做近似动态规划：

      

       7.收缩映射定理

        关于收缩映射定理的具体介绍见泛函分析的教材，这里就不赘述了，定理如下：

      

        该定理可以用于证明策略迭代、值迭代的收敛性，具体证明就不在这列出来咯～

       

        最后关于动态规划的扩展以及收缩映射定理证明迭代性说得比较笼统，有什么问题可以留言哈～