算法实验五：图论——桥，从零开始带你读懂各种找桥算法思路（基准法，并查集法，并查集+LCA环边法）
文章目录
- 零、实验内容
- 一、什么是桥？
- 二、基准法求桥的边数
- 2.1为什么用邻接表而不用邻接矩阵？
- 2.2基准法算法思路
- 2.3如何计算连通分量
- 2.4如何删除边
- 2.5伪代码
- 2.5.1 DFS伪代码：
- 2.5.2 求连通分量伪代码：
- 2.5.3 求桥的个数伪代码：
- 2.6 基准法优化
- 三、并查集求桥的个数
- 3.1 什么是并查集？
- 3.2 并查集找桥思路
- 3.3 并查集+高度优化
- 3.3.1 并查集+高度优化整体思想
- 3.3.2 并查集+高度优化 伪代码
- 3.4 并查集+路径压缩
- 3.4.1 并查集+路径压缩整体思想
- 3.4.2 并查集+路径压缩伪代码
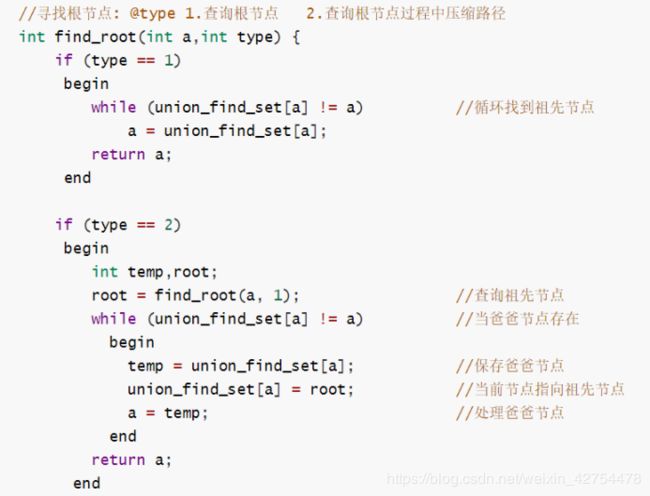
- 四、并查集+LCA环边求桥的个数
- 4.1并查集+LCA环边求桥整体流程
- 4.2 LCA找最小公共祖先和环边
- 4.2.1 非生成树边与并查集
- 4.2.2 边11-15的LCA具体步骤
- 4.2.3 以点代边数组记录遍历过的环边
- 4.3 代码实现
- 4.3.1 创建生成树代码实现
- 4.3.2 LCA代码实现 (拿左高度大于右高度的情况举例)
本文主要记录几种在无向图中找桥的算法，希望以简单易懂的方式加形象的图解带你读懂复杂的算法。
零、实验内容
本实验要求求出一个无向图中所有的桥。
1.使用基准算法找桥。
2.应用并查集设计一个比基准算法更高效的算法。不要使用Tarjan算法，如果使用Tarjan算法，仍然需要利用并查集设计一个比基准算法更高效的算法。
一、什么是桥？
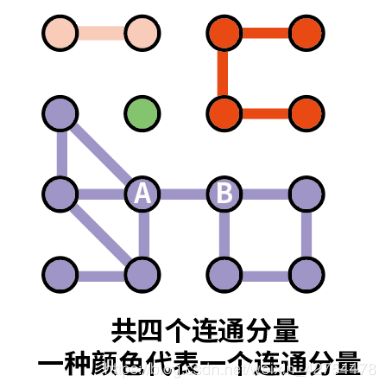
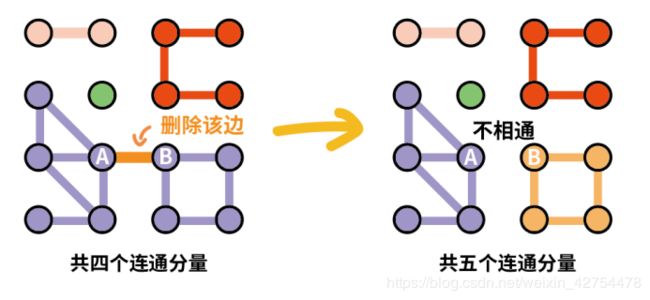
- 桥的定义：若删除当前边后无向图的连通分量增加，则当前边为桥。
- 桥的理解：
- 下图所示含有四个联通分量，同一个连通分量的任意两个节点都可通过其联通分量内的边到达：
- 如果我们将AB这一条边删除掉，会发现AB之间不再联通，图由四个连通分量变成五个联通分量。与桥的定义：“删除该边则连通分量增加”相符合，故AB这条边是桥。
二、基准法求桥的边数
2.1为什么用邻接表而不用邻接矩阵？
首先需要明确的是，由于实验数据或者说求桥的实际应用中的数据多为稀疏数据，若使用邻接矩阵创建图则会得到稀疏矩阵，在大数据的情况下是非常消耗空间的。所以我们这里牺牲了稀疏矩阵查询数据的O(1)时间复杂度来节省大量创建图的空间，选择创建邻接表。
2.2基准法算法思路
首先计算原邻接表里面连通分量的个数A，然后对于无向图的每一条边都进行以下操作：*
(1) 将该边从邻接表删除
(2) 计算删除边之后邻接表的连通分量个数B
(3) 将删除的边加回来
(4) 若A≠B，则表示当前边为桥，否则当前边不是桥
2.3如何计算连通分量
整体思路：首先创建长度大小等于节点个数的访问数组，并对每个元素初始化为0，然后对每个节点进行以下操作：
(1) 若当前节点对应的访问数组的值等于1，则遍历下一个节点
(2) 若当前节点没被访问，连通分量个数加1，同时对该节点进行DFS遍历，将遍历过程中的点对应访问元素的值设置成1
经过了上面的步骤之后即可求出联通分量的个数，下面进行图解：
(1) 刚开始联通分量为0，且每个节点均未被访问过
(2) 对A点进行DFS，点亮其联通分量的其他节点（访问值设置成1），同时连通分量加1
(3) 同理访问到B、C、D三点时点亮对应的节点，同时联通分量加1
(4) 最后得到四个联通分量
2.4如何删除边
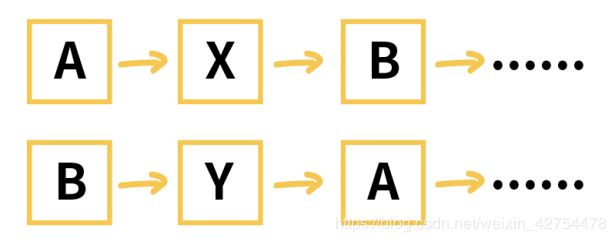
整体思路：由于我们用邻接表的形式存储边，所以对于无向图来说，AB这条边其实存在于无向图的两个位置：A->B,以及B->A。所以我们需要进行特殊处理，防止一条边被计算了两次。下图表示AB边在邻接表的表示，其中X，Y为邻接表的其他节点。
例子讲解：
对于下图来说：首先我们需要对所有边的flag初始化为0，并对访问数组进行一次初始化为0（每次删除边都需要初始化）：
(1) 由于我们是在邻接表里面遍历边然后进删除操作，例如我们遍历到了绿色圆圈对应的A->B边，表示这是A-B边，发现其flag等于0，说明没被删除过，此时将A->B以及B->A两条边的flag都设置成1，然后计算其联通分量。
(2) 注意！此时计算连通分量中用到的DFS遍历需要加多一个条件：若访问到当前边的flag等于1，则不再递归，因为这表示当前遍历到的边是被我们删除的边。
(3) 计算完联通分量之后将A->B,B->A两条边的flag设置成2。
(4) 访问其他边…
(5)当删除边的过程访问到了B->A的时候，此时发现B->A的flag等于2，说明之前已经被删除过了，所以跳过当前边。
2.5伪代码
2.5.1 DFS伪代码：
2.5.2 求连通分量伪代码：
2.5.3 求桥的个数伪代码：
2.6 基准法优化
我们发现使用上面的方法判断是否是桥，对于每条边的判断都需要计算一次删除边之后的连通分量，而连通分量的计算实际上又需要遍历每一个节点，可见耗时非常大。因此思考下面的改进思路：
- 首先删除边的方法与前面一样，都是根据标志位来判断是否需要进行DFS，改进点在于删除边之后进行DFS，我们只需要判断是否还有其他路径使得删除边对应的两个点能够连通：
1. 对删除边的其中一个点进行DFS，判断DFS之后另一个点是否被访问，如果被访问，则说明该边不是桥。
2. 同时在DFS过程中，如果发现已经遍历到了另一个点（判断肯定不是桥），则提前退出DFS。
该方法相比于之前的方法，只需要对一个点进行DFS则可以判断该边是否为桥，同时DFS过程中发现不是桥马上退出，不需要进行不必要的遍历，而之前的方法需要对所有的边进行DFS。
三、并查集求桥的个数
3.1 什么是并查集？
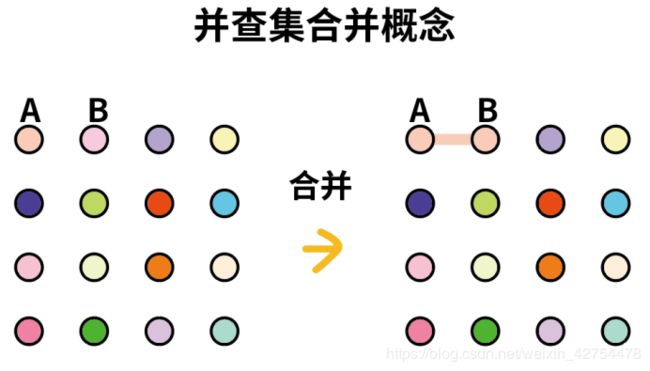
并查集是一种可以动态维护若干个不重叠的集合，并支持合并与查询两种操作的一种数据结构。
(1) 所谓合并，即将一个集合的元素合并到另一个集合里面去。
(2) 所谓查询，即查看当前元素属于哪一个集合。
下图所示为合并两个集合的例子：
3.2 并查集找桥思路
(1) 设计一个并查集数组，让每一个元素都能够指向它能表示的根节点点（不一定是直接指向根节点）。
(2) 首先在创建邻接表的过程中动态创建该并查集数组，并求得初始情况的连通分量个数。然后对每条边进行下面的操作：
删除该边之后生成新的并查集数组，求新的并查集数组的连通分量个数。判断两个数组的连通分量个数是否相同：
① 若相同，则该边不是桥
② 若不相同，则是桥
3.3 并查集+高度优化
由于并查集的创建和查询需要多次遍历并查集数组，而并查集数组实质上是一颗树，因此如果我们能够尽可能降低并查集的树高度，就能提高并查集的查询效率。
上面提到了我们需要创建并查集用于桥的判断，那么什么样的并查集在后续进行桥的判断会比较快呢？树高度优化法是一种方法。下面详细说一下
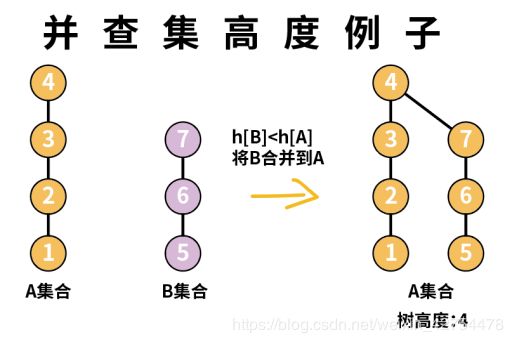
首先需要设立一个树高度的数组h，用来表示该元素对应的树的高度。比如我们进行下面的合并：
例如集合A的高度为4，集合B的高度为3，所以集合B的高度小于集合A，故将集合B合并到集合A。
3.3.1 并查集+高度优化整体思想
首先在创建邻接表的过程中把并查集建立起来，建立过程中若遇到两个不一样的集合A和集合B，则进行下面的判断：
(1) 计算出A，B两个集合的根节点的高度hA，hB。
(2) 若hA>hB,将集合B合并到集合A
(3) 若hA
3.3.2 并查集+高度优化 伪代码
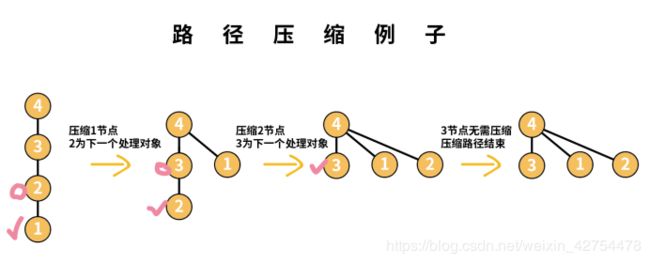
3.4 并查集+路径压缩
考虑到在合并过程中每次都需要寻找当前元素对应的祖先节点，而树的高度越大，祖先节点寻找得就越慢，除了上面的方法外，也可通过路径压缩的方式降低树的高度。
3.4.1 并查集+路径压缩整体思想
实际上路径压缩也有很多种方法，下面我介绍其中一种，主要希望说下思想是什么，至于具体的路径压缩算法怎么设计更高效还需要实际测试数据来确定。
在查询某元素的过程中，将过程中的所有元素均指向根节点。我们拿下图的例子举例：
(1) 当我们查询节点1的根节点时，首先记录其父亲节点2，并调用一次查询函数找到祖先节点4.然后将1指向4
(2) 接着处理父亲节点2，记录2的父亲节点3，并将2指向4
(3) 发现3的祖先节点为4，路径压缩结束
3.4.2 并查集+路径压缩伪代码
四、并查集+LCA环边求桥的个数
实际上上面介绍的算法在实验过程中面对大数据的时候非常无力，因为实在是太慢了啊。那么有没有更快一点的方法咧？有！下面我来介绍一下并查集+LCA环边找桥的算法思路。先不要被这么多复杂的名词吓到，下面我一个个解释。
4.1并查集+LCA环边求桥整体流程
首先给出我整理的该算法的一个思维导图，下面再进行详细解释：
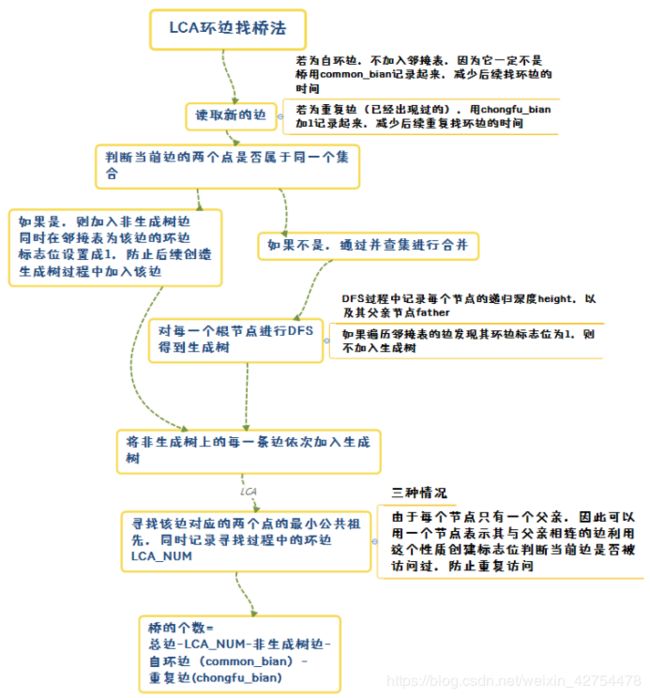
并查集+LCA环边求桥算法整体思路：
- 输入边的过程中创建并查集和邻接表。
- 若为自环边（自己指向自己）和重复边（已经出现过一次），用两个变量记录这两种类型边的数目，不纳入邻接表，减少后续找环边的时间。
- 若通过并查集判断当前输入边的两个节点在一个集合，则判定为非生成树边，将这条边的环边特殊标志位设定为1。
- 访问并查集对每个根节点进行DFS构建生成树
- 对每个节点记录其递归深度（在生成树上的高度）和其父亲节点（开始默认其父亲节点为自身）
- 若当前边的环边特殊标志位设定为1，则不进行下一层的DFS（因为它属于非生成树边，不能纳入生成树噢）
- 将每一条非生成树边加入生成树，通过LCA方法寻找该边的两个点的最小公共祖先，并将寻找过程中遇到的环边用LCA_NUM记录下来，同时设置该边的访问标志位为已访问，防止之后的边进行LCA遇到已经遍历过的边重复记录。
（ 注：由于生成树中，每个非根节点必定有且只有一个父亲节点，因此我们可以**用以点代边的方式，创建一个大小为节点数目的访问数组，每个节点表示其与父亲节点相连的边。**这样子当我们进行LCA的时候，对寻找最小公共祖先过程中遇到的环边，将访问数组中该环边中高度更高的节点（孩子节点） 设置成1，就能防止之后重复记录环边了。） - 最终桥的数量=总边-自环边-重复边-LCA记录的环边（LCA_NUM）-非生成树边（输入数据时候记录的）
4.2 LCA找最小公共祖先和环边
上面的整体思路介绍中多次提到了LCA，那么究竟什么是LCA呢？如何实现呢？怎么和并查集联系起来呢？下面就来详细讲讲它的原理。
4.2.1 非生成树边与并查集
同样，我们拿下图这个具体的例子进行介绍：
首先回顾一下上面1，2步的内容，在输入边的过程中我们需要找到非生成树边以及创建并查集。
比如下面这个例子中，我们找到了三条黄色的非生成树边（4，9），（9，13），（11，15）。（注意！如果输入边的顺序不同可能得到的是另外的边，这里只是举个例子）：
比如在输入边（4，9）的时候，我们发现4和9都在紫色集合里面（因为边4-8，边8-9这两条边把4和9合并到了同一个集合里面），因为如果此时把边4-9加进来，节点（4-8-9）就会形成一个环，因此我们把边（4，9）加入非生成树边（在邻接表中用一个标志位表示）。
下一步是创建生成树。我们需要搜索第一步创建的并查集，找到每个根节点，然后对每个根节点都进行DFS遍历，遍历过程中记录每个节点的父亲节点和其所在的树的高度。可得到下图右边的生成树（注意！这里的生成树其实是用并查集数组表示的，而不是真正意义上的数据结构的树结构）
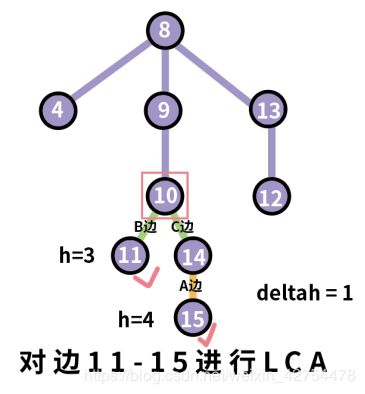
得到生成树之后，我们需要将每条非生成树边依次加入生成树。对于这条边的两个节点，寻找它们的最小公共祖先节点，并且将寻找过程中遇到的边记录下来。下面我们拿（11，15）这条边进行解释。
4.2.2 边11-15的LCA具体步骤
1.“降高度”：节点15的高度为4，节点11的高度为3，它们的高度差为1.所以首先需要对节点15沿着父亲节点遍历，直到其高度为3（与11的高度一样）。于是我们首先找到A边。
2.“共同前进”：此时节点11和节点14的高度都为3，然后让它们同时寻找父亲节点10，记录下来B边和C边。
3.“找到同一个祖先”：我们发现节点11和节点14的父亲节点一样，即节点10为节点11和15的最小公共祖先。
4.上面提到了一个细节，就是节点11和节点15的高度不一致，所以首先需要对高度大的节点进行降高度（找到其父亲节点，同时记录该点跟父亲节点相连的这条边），直到其高度跟另一个节点一样。再进行找祖先。
上面说的这个就是LCA的核心！！注意一点，上面找到的A，B，C都是环边，我们需要记录下来环边的数量。
实际上LCA有三种情况：我们设非生成树边的两个节点为A，B：
(1) A的高度>B的高度，需要先对A进行降高度
- 降高度并不是说把A节点的高度改变，而是通过找父亲节点的方式找到跟B节点同高度的节点操作使得其与B的高度一致，然后再同时寻找公共祖先
(2) B的高度>A的高度，与第一种情况一样，先对B进行降高度，再寻找最小公共祖先节点（找到的第一个相同的父亲节点）
(3) A的高度=B的高度，不需要进行降高度，直接寻找父亲节点
4.2.3 以点代边数组记录遍历过的环边
由于不同的非生成树边都会进行“找环边”的操作，因此同一条环边可能被遍历多次，但是我们需要防止一条边被记录多次，不然就算重复了，算多了。而实际上我们的生成树是以并查集数组的形式储存的，也就是说数组的每个元素代表着一个点，那么我们如何通过表示边呢？下面主要来讲讲这个。
- 以点代边数组：
- 对于生成树来说，除了根节点外，其余所有节点有且仅有一个父亲节点。因此生成树上的每一条边其实都可以用这条边的孩子节点来表示。这就是以点代边数组的整体思路。
我们拿下图举例子：比如访问边15-14，由于节点15只有一个父亲节点，所以我们可以用以点代边数组中下标为15元素表示边15-14（A边）.同理下标为11的元素表示边11-10（B边）,下标为14的元素表示边14-10（C边）.
当我们进行LCA的过程中，在对当前节点进行“找父亲”的操作时，只需要将当前节点在以点代边数组中对应的值设置成1，则表示被访问过，同时环边个数加上1（单独拿一个变量存环边的个数）即可。
当之后的找环边过程中如果再次访问到了A边，我们通过以点代边数组可发现其值为1，表示已经被访问过，这时总环边数目就无需增加。
4.3 代码实现
4.3.1 创建生成树代码实现
4.3.2 LCA代码实现 (拿左高度大于右高度的情况举例)
