字节跳动-文远知行杯 广东工业大学第十四届程序设计竞赛（7题）

A - hzy 和 zsl 的生存挑战

这道题很有意思啊，在不知道答案的情况下很多人在比赛的时候可能会很着急就难以考虑到方方面面，其实只需要一个人说自己听到的数字，另一个人说与自己听到数字相反的数字，就一定能活下来。

这题就没必要附上代码了。

G - 简单数学题

这道题数据量很大，显然是需要推公式的。
我们将公式拆分开后，就会得到这样一个式子：

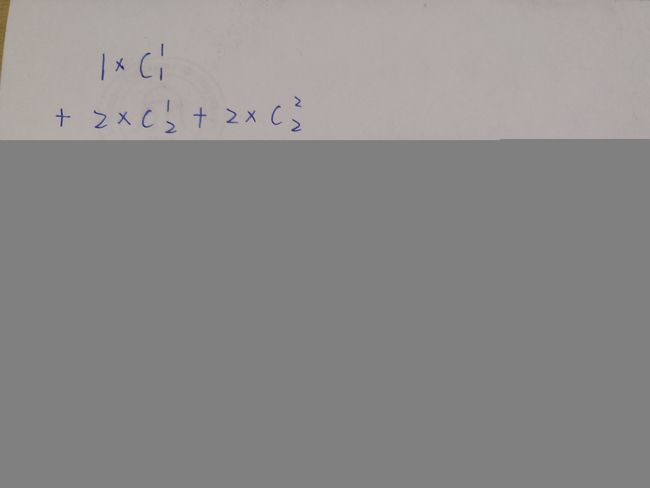
那么如何计算他们呢？这里就需要一些数学公式了

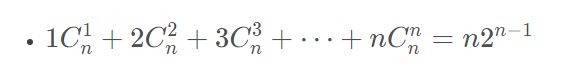
有了这个式子，上面就会变成
至于这个式子的运算，想必大家高中的时候就已经练得炉火纯青了吧
最后得到的公式是这样的：

（n - 1）*2^n + 1

#include
using namespace std;
#define maxn 300005
#define ll long long
#define lll __int128

const int mod=1e9+7;
ll n;
ll poww(ll a,ll b){
    ll ans=1,base=a%mod;
    while(b!=0){
        if(b&1!=0)ans=(ans*base)%mod;
        base=(base*base)%mod;
        b>>=1;
    }
    return ans%mod;
}
int main()
{
	while(~scanf("%lld",&n)){
		ll sum=(((n-1)%mod)*poww(2,n))%mod+1;
		printf("%lld\n",sum%mod);
	}
	return 0;
}

B - 人类史上最大最好的希望事件

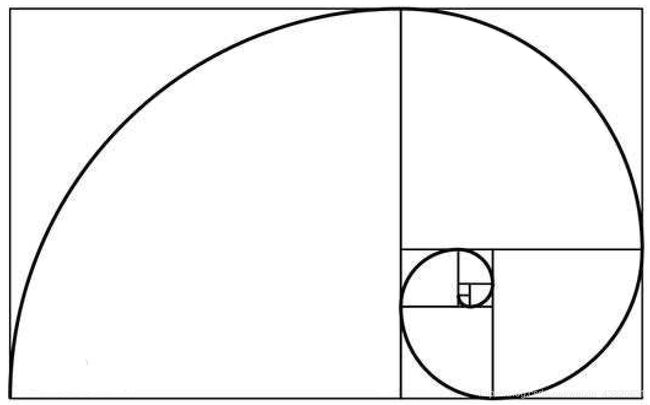
斐波那契螺旋线
就是经过的正方形的边长是按斐波那契数列排列的。这里我们开两个数组，一个存正方形的边长，一个存从0开始到a+b/4经过正方形的面积。预处理好这点应该就没什么问题了。

#include
using namespace std;
#define maxn 50005
#define ll long long
const ll mod=192600817;

int t,a1,b1,a2,b2;
ll f[maxn],sum[maxn];

void init(){
	f[0]=f[1]=1;
	sum[0]=0;sum[1]=2;
	for(int i=2;i<maxn;i++){
		f[i]=(f[i-1]+f[i-2])%mod;
		sum[i]=(sum[i-1]+f[i]*f[i]%mod)%mod;
	}
}
int main()
{
	init();
	while(~scanf("%d",&t)){
		while(t--){
			scanf("%d %d %d %d",&a1,&b1,&a2,&b2);
			int s1=4*a1+b1,s2=4*a2+b2;
			if(s1>s2)swap(s1,s2);
			if(s1!=0)printf("%lld\n",((sum[s2]-sum[s1]+mod)%mod+f[s1]*f[s1]%mod) % mod);
			else printf("%lld\n",(sum[s2]-sum[s1]+mod)%mod);
		}
	}
	return 0;
}

C - 超级无敌简单题

这题暴力打表，打到120W，就能差不多得到15W个鸽子数了

#include
using namespace std;
#define maxn 150005

int t,x,n,sum,cnt;
int a[150005];
int main()
{
    a[++cnt]=1;
    for(int i=2;i<=1200000;i++){
        n=i;
        while(n!=1&&n!=4){
            sum=0;
            while(n>0){
                sum+=(n%10)*(n%10);
                n/=10;
            }
            n=sum;
        }
        if(n==1)a[++cnt]=i;
        if(cnt==150000)break;
    }
    scanf("%d",&t);
    while(t--){
    	scanf("%d",&x);
    	printf("%d\n",a[x]);
	}
    return 0;
}

J - Count

这题队友写的，矩阵快速幂，（我不是很懂，逃 ）
直接上代码了：

#include 

using namespace std;

typedef long long LL;

#define MOD 123456789LL
#define endl '\n'
#define MAX_N 6

template<typename T, int N = 1>
struct Matrix {
    Matrix(int f = 0) : n(sizeof(data[0]) / sizeof(data[0][0])) {
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                data[i][j] = T(0);
        if (f)
            for (int i = 0; i < n; data[i][i] = T(1), ++i) {}
    }

    Matrix operator * (const Matrix& other) const {
        Matrix<T, N> ret;
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                for (int k = 0; k < n; k++)
                    ret.data[i][j] = (ret.data[i][j] + data[i][k] * other.data[k][j] % MOD) % MOD;
        return ret;
    }

    Matrix operator + (const Matrix& other) const {
        Matrix<T, N> ret;
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                ret.data[i][j] = (data[i][j] + other.data[i][j]) % MOD;
        return ret;
    }

    Matrix& operator % (const LL mod) {
        return *this;
    }

    T data[N][N];
    int n;
};

template<typename T>
T mul(T a, LL n, LL mod)
{
    T ret(1);
    for (; n; n >>= 1) {
        ret = ret * (n & 1 ? a : T(1)) % mod;
        a = a * a % mod;
    }
    return ret;
}

const LL modulu[MAX_N][MAX_N] = {
    {1, 2, 1, 3, 3, 1},
    {1, 0, 0, 0, 0, 0},
    {0, 0, 1, 3, 3, 1},
    {0, 0, 0, 1, 2, 1},
    {0, 0, 0, 0, 1, 1},
    {0, 0, 0, 0, 0, 1}
};

int main()
{
    int T;
    cin >> T;
    for (LL n; T--; ) {
        cin >> n;
        n --;
        if (n <= 1) {
            cout << n +1<< endl;
            continue;
        }
        Matrix<LL, MAX_N> a;
        memcpy(a.data, modulu, sizeof(modulu));
        a = mul(a, n - 1, MOD);
        cout << (a.data[0][0] * 2 + a.data[0][1] * 1 + a.data[0][2] * 8 +
                a.data[0][3] * 4 + a.data[0][4] * 2 + a.data[0][5]) % MOD << endl;
    }
    return 0;
}

F - 清一色

队友写的超大型模拟题，我。。。不会写
上代码：

#include
using namespace std;
const int mod = 192600817;
#define ll long long
const int maxn = 10005;
int shun,ke , pai[10],paire[10];
int ff=0;
void init(){
	for(int i=1;i<=9;i++){
		pai[i]=paire[i];
	}
	ke=0,shun=0;ff=0;
}
void kezi(int num);
void shunzi(int num);
void judge();
bool dui(){
	int ans=0;
	for(int i=1;i<=9;i++){
		if(pai[i]==2)ans++;
	}
	if(ans==7)return 1;
	else return 0;
}
bool work(){
		init();
		if(dui())return 1;
		init();
		shunzi(0);
		kezi(0);
		if(ff)
		return 1;
		else return 0;
}
int main(){
	int n, pppp = 0;
    for(int i = 1 ; i <= 150 ; ++ i) pppp ++;
	int num,flag;
	while(~scanf("%d",&n))
	{
		for(int i=1;i<=9;i++)
		{
			paire[i]=0;
		}
		if(n==0)break;
		else paire[n]++;
		int x;
		flag=0;
			for(int i=1;i<=13;i++){
				scanf("%d",&x);
				paire[x]++;
			}
		if(work()){
			printf("tsumo\n");
			continue;
		}
		for(int i=1;i<=9;i++)
		{
			num=0;
			for(int j=1;j<=9;j++){
				if(paire[i]>=1&&paire[j]<4&&i!=j)
				{
					paire[i]--,paire[j]++;
					if(work()){
						flag++;
						if(flag==1)printf("tenpai");
						if(num==0)
						{
							printf("\n%d:",i);
							num++;
						}
						printf(" %d",j);
					}
					paire[j]--,paire[i]++;
				}
			}
		}
			if(flag==0)
			printf("noten\n");
			else printf("\n");
	}
	return 0;
}
void shunzi(int num){
	if(num==4)
	{
		judge();
	}
	for(int i =1 ;i <= 9;i++){
			if(pai[i]>=3)
			{
			pai[i]-=3;
			shunzi(num+1);
			kezi(num+1);
			pai[i]+=3;
			}
	}
}

void kezi(int num){
	if(num==4)
	{
		judge();
	}
	for(int i =1 ;i <= 7;i++){
			if(pai[i]&&pai[i+1]&&pai[i+2]){
				pai[i]--;
				pai[i+1]--;
				pai[i+2]--;
					shunzi(num+1);
					kezi(num+1);
				pai[i]++;
				pai[i+1]++;
				pai[i+2]++;
			}
		}
	}
void judge(){
	for(int i=1;i<=9;i++)
	{
		if(pai[i]==2)ff = 1;
	}
}

H - zyb的面试

这题需要用字符串排序，按理说string可以直接排序，但我不知道怎么回事就是跑不出来，最后换了char，排序时要用strcmp()函数判断两个字符串的大小。
这题我们可以直接预处理1——>1e6，按新字典序排个序，最后碰到>n的直接跳过，
碰到<=n的k–，k == 0的时候跳出循环，输出那个数即可。

#include
using namespace std;
#define ll long long
#define maxn 1000001

int T,n,k;
struct zfc{
    int num;
    char s[7];
}a[maxn];
bool cmp(zfc x,zfc y){
    return strcmp(x.s,y.s)<0;
}
void init(){
	for(int i=1;i<maxn;i++){
        a[i].num=i;
        int t=i,e=0,m;
        while(t>0){
            a[i].s[e++]=t%10+'0';
            t/=10;
        }
        for(int j=0;j<e/2;j++){
            char ch=a[i].s[j];
            a[i].s[j]=a[i].s[e-j-1];
            a[i].s[e-j-1]=ch;
        }
    }
    sort(a+1,a+maxn,cmp);
}
int main()
{
	init();
    scanf("%d",&T);
    while(T--){
        scanf("%d %d",&n,&k);
        int i;
        for(i=1;i<maxn;i++){
            if(a[i].num>n)continue;
            else k--;
            if(k==0)break;
        }
        printf("%d\n",a[i].num);
    }
    return 0;
}