2020杭电多校 Fibonacci Sum 数论
链接
http://acm.hdu.edu.cn/showproblem.php?pid=6755
题意
题解
根据公式
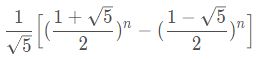
首先要知道通项公式且能将其转化为mod意义下整数(解二次同余方程)。
得出:
A = 691504013((1+根号5)/2), B = 308495997((1-根号5)/2);
sqrt5 = 383008016(根号5), invsqrt5 = 276601605(根号5分之一)
将每一项展开,观察到纵向为一个n+1项的等比数列,等比数列求和可以有优化掉些快速幂,
#include<stdio.h>
#include<algorithm>
#include<math.h>
using namespace std;
#define ll long long
const ll mod = 1e9+9;
const int maxn = 1e5+5;
// 逆元
ll A = 691504013, B = 308495997;
ll sqrt5 = 383008016, invsqrt5 = 276601605;
ll fac[maxn], f[maxn], inv[maxn];
//快速幂模板
ll qpow(ll a, ll n)
{
ll res = a%mod, sum = 1;
while(n)
{
if(n&1) sum = (sum*res)%mod;
res = (res*res)%mod;
n >>= 1;
}
return sum;
}
//数据预处理
void init()
{
fac[1] = 1;
f[1] = 1;
inv[1] = 1;
for(ll i = 2; i <= 100000; i++)
{
fac[i] = fac[i-1]*i%mod;//计算阶乘
f[i] = (mod - mod/i)*f[mod%i]%mod;
inv[i] = inv[i-1]*f[i]%mod;//计算阶乘逆元
}
}
//计算组合数 C(m,n)=m!/n!(m-n)!
ll C(ll m, ll n)
{
if(m < n) return 0;
if(n == 0 || m == n) return 1;
return fac[m]*inv[n]%mod*inv[m-n]%mod;
}
ll sac[maxn], sbc[maxn];
int main()
{
init();
int t;
scanf("%d", &t);
while(t--)
{
ll n, c, k;
scanf("%lld%lld%lld", &n,&c,&k);
// n = 1e18, c = 1e18, k = 1e5;
ll res = qpow(invsqrt5, k);
ll ans = 0, flag = -1;
ll x, y;
ll ac = qpow(A, c), bc = qpow(B, c);
sac[0] = 1, sbc[0] = 1;
sac[1] = ac, sbc[1] = bc;
for(int i=1; i<=k; i++)
{
sac[i] = sac[i-1]*ac%mod;
sbc[i] = sbc[i-1]*bc%mod;
}
ll acn = qpow(qpow(A, c), n);
ll bcn = qpow(qpow(B, c), n);
ll invacn = qpow(acn, mod-2);
ll invbcn = qpow(bcn, mod-2);
ll now_acn = qpow(acn, k), now_bcn = 1;
for(ll i = 0; i <= k; i++)
{
flag *= -1;
ll q = sac[k-i] * sbc[i] % mod;
if(q == 1)
{
q = (n%mod)*C(k, i) % mod;
ans = (ans + flag*q%mod + mod) % mod;
}
else
{
x = (C(k, i)*sac[k-i]%mod) * sbc[i] % mod;
x = (1-(now_acn * now_bcn % mod) + mod) % mod * x % mod;
y = (1 - (sac[k-i] * sbc[i])%mod ) % mod;
y = qpow(y, mod-2);
ans = (ans + flag*x*y%mod + mod)%mod;
}
now_acn = (now_acn * invacn) % mod;
now_bcn = (now_bcn * bcn) % mod;
}
printf("%lld\n",ans*res%mod);
}
return 0;
}