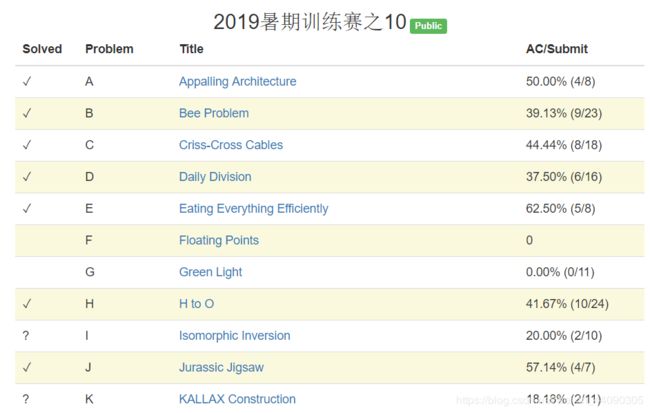
HNU 2019暑期训练赛之10
J. Jurassic Jigsaw
Problem Description
The famous Jurassic park biologist Dean O’Saur has dis- covered new samples of what he expects to be the DNA of a dinosaur. With the help of his assistant Petra Dactil, he managed to sequence the samples, and now they are ready for analysis. Dean thinks this dinosaur was affected with a particular disease mutating the DNA of some cells.
To verify his theory, he needs to compute the most likely evolutionary tree from the samples, where the nodes are the samples of DNA. Because there is no temporal data of the DNA samples, he is not concerned where the root of the tree is.
Dean considers the most likely evolutionary tree, the tree with smallest unlikeliness: the unlikeliness of a tree is defined as the sum of the weights of all edges, where the weight of an edge is the number of positions at which the two DNA strings are different.
As a world expert in data trees, he asks you to reconstruct the most likely evolutionary tree.
In the first sample, the optimal tree is AA - AT - TT - TC . The unlikeliness of the edge between AA and AT edge is 1, because the strings AA and AT differ in exactly 1 position. The weights of the other two edges are also 1, so that the unlikeliness of the entire tree is 3. Since there is no tree of unlikeliness less than 3, the minimal unlikeliness of an evolutionary tree for this case is 3.
Input
• The first line consists of two integers 1 ≤ n ≤ 1000 and 1 ≤ k ≤ 10, the number of samples and the length of each sample respectively.
• Each of the next n lines contains a string of length k consisting of the characters in
ACTG.
Output
• On the first line, print the minimal unlikeliness of the evolutionary tree.
• Then, print n − 1 lines, each consisting of two integers 0 ≤ u, v < n, indicating that in the most likely evolutionary tree, there is an edge between DNA string u and v. If there are multiple answers possible, any of them will be accepted.
Sample Input
4 2
AA
AT
TT
TC
Sample Output
3
0 1
1 2
2 3
Sample Input2
4 1
A
A
G
T
Sample Output2
2
0 1
0 2
0 3
Sample Input3
5 6
GAACAG
AAAAAA
AACATA
GAAAAG
ATAAAT
Sample Output3
7
0 3
1 2
1 3
1 4
Solution
最小生成树
AC Code
#includeE. Eating Everything Efficiently
Problem Description
Margriet A. is in pizza heaven! She has bought a one- day access pass to Pizza World. Pizza World is a food festival, where all stands have their own special type of pizza. Margriet would really like to try many different types of pizza, but she thinks that she can only eat two pizzas in total. Therefore, she has come up with a cunning plan: at each stall she visits she decides whether she wants to buy this pizza or not. At the first stall where she decides to make a purchase, she will buy and eat exactly one pizza. At the second one, she will buy and eat half a pizza, and at the third she will eat one quarter of a pizza, etc… Therefore, at the kth stall where she
decides to buy some pizza, she will eat 1/(2^{k-1})th1/(2
k−1
)th part of a pizza. This way she makes sure that she will never get full!
In order to ensure that the flow of people in the park is adequate, the pizza stalls are connected by one-way paths, and to make sure that everyone will leave the festival, it is made impossible to visit a pizza stall more than once. However, every stall can be reached from the stall at the entrance, which is the stall with number 0.
Of course, Margriet has her own taste: she will like some pizzas more than others. Eating pizza from a stall will give her a certain amount of satisfaction which is equal to Margriet’s personal stall satisfaction number multiplied by the fraction of a whole pizza she eats there. Her total satisfaction is the sum of satisfactions of every stall she visits. Can you help Margriet plot a route between the pizza stalls that satisfies her the most?
Input
• Two integers 1 ≤ n ≤ 5 · 10^51≤n≤5⋅10
5
and 0 ≤ m ≤ 5 · 10^50≤m≤5⋅10
5
, the number of pizza stalls and the number of one way connections.
• The second line has n integers cc0, . . . , ccn−1, 0 ≤ c_i ≤ 10^90≤c
i
≤10
9
, the amount of enjoyment Margriet gets from eating one pizza at stall i.
• The next m lines each contain 2 integers 0 ≤ s < n and 0 ≤ t < n, indicating a one way path from stall s to stall t. No connection will appear twice in the input.
Output
• Print the maximal amount of enjoyment Margriet can reach at the pizza fair. Your answer will be considered correct if it differs from the actual answer by at most 10^{−6}10
−6
absolutely or relatively.
Sample Input
5 5
1 4 6 2 100
0 1
1 2
0 3
2 4
3 4
Sample Output
100
Sample Input2
3 2
1 0 1
0 1
1 2
Sample Output2
1.5
Sample Input3
3 2
3 2 1
0 1
1 2
Sample Output3
4.25
Solution
dp
AC Code
#include D. Daily Division
Problem Description
Oostende Beach is a very long beach located in the north of Belgium. On this beach, there are n huts located along a straight line. People can rent a room in one of those huts to spend their beach vacations together with the other tenants.
Every day at lunch time, a food truck rides by to serve fries to the guests. The truck will park in front of one of the huts and people will form two queues. The people staying in huts to the left of the food truck will queue on the left, and the people to the right of the food truck will queue together on the right. The people staying in the hut in front of the food truck will split their group in half, one half going to the left queue and the other half going to the right queue. If this is an odd number of people, the remaining person will go to the queue with fewer people, or choose one randomly if the queues have the same length. The food truck will always position itself so that the difference between the number of people in the left queue and the number of people in the right queue is as small as possible.
Each night the number of guests in exactly one of the huts changes. Can you help the food truck find the best position for each day?
Input
• The first line of the input consists of two integers 1 ≤ n ≤ 10^51≤n≤10
5
, the number of huts, and 1 ≤ q ≤ 10^51≤q≤10
5
, the number of days.
• The second line has n integers aa0, . . . , aan−1 satisfying 1 ≤ a_i ≤ 10^61≤a
i
≤10
6
for 0 ≤ i < n, where a_ia
i
is the current number of people in hut i.
• Then follow q lines with two integers 0 ≤ i < n0≤i
. The jth of these lines indicates that at day j the number of people in hut i changes to x.
Output
• Print q lines: the optimal position of the foodtruck after each of the q nights. If there are multiple optimal positions, print the smallest one.
Sample Input
5 4
3 1 3 4 2
0 5
0 9
4 5
2 1
Sample Output
2
1
2
1
Sample Input2
4 8
1 1 1 1
2 2
1 2
2 1
1 1
3 2
2 2
1 2
2 1
Sample Output2
1
1
1
1
1
2
2
2
Solution
用树状数组维护区间
每一次访问 二分查找人数一半的位置即可
坑点就是 。。 解不唯一时优先选小的。。
连WA了我好几发。。。
AC Code
#includeAppalling Architecture
Problem Description
You have recently been hired as an architect for the BAPC (Bureau of Architecture and Promising Constructions), re- sponsible for top-quality buildings such as the Tower of Pisa. However, in the past couple of weeks, some of the constructions that the BAPC has made have collapsed! It is up to you to figure out whether any other constructions are in danger.
After some research it seems like the x-coordinate of the center of gravity of some of the constructions is off: if this is too much to the left or to the right, the construction will fall over. Hence, you decide to check all the blueprints and see whether the constructions are stable or not.
Given is an up to 100 by 100 grid of characters in .#/_|-. The . characters denote empty space, while each other character represents a completely filled 1 × 1 box (any difference in symbols used is due to the artistic freedom of the other architects), whose center of mass is at the center of the box.
Every construction forms a single connected component that touches the ground, i.e. the bottom layer of the grid.
The construction falls to the left if the x-coordinate of the center of gravity is less than the x-coordinate of the leftmost point of the construction that touches the ground, and it falls to the right if the x-coordinate of the center of gravity is larger than the x-coordinate of the rightmost point of the construction that touches the ground. It is guaranteed that the center of gravity is never exactly above the leftmost or rightmost point where the building touches the ground.
Given a blueprint, is the construction balanced, does it fall to the left, or does it fall to the right?
Input
• The first line has 1 ≤ h ≤ 100 and 1 ≤ w ≤ 100, the height and width of the grid.
• Then follow h lines with l characters each. Each character is either ., indicating empty space, or one of #/_|-, indicating a filled 1 × 1 box .
Output
• Print a single line containing left, balanced, or right.
Sample Input
3 3
/-
|.|
#.#
Sample Output
balanced
Sample Input2
3 3
…
…|
Sample Output2
left
Sample Input3
3 3
./
./
.|.
Sample Output3
balanced
Sample Input4
20 19
…
…-—…
…/////-.
…–//##/…
…////////.
…-/#######/-.
…/////##/…
…/##/////…
…/######/…
…/////////-…
…/########/-…
…////##/…
…/#/#///…
…/#######/-…
…/////////-…
…/####/-…
…///\#/-…
…//////////-…
…////##////-…
.-##_…
Sample Output4
balanced
Solution
这题题目有趣 虽然一开始没读懂
读懂了还是蛮简单的 直接计算重心 然后按题意比较就行
AC Code
#include<bits/stdc++.h>
using namespace std;
int const maxn = 105;
char graph[maxn][maxn];
int h, w;
int leftMost = 0x3f3f3f3f, rightMost = -1;
#define eps 1e-7
bool isBlock(char &c) {
bool flg = (c == '#' || c == '/' || c == '_' || c == '|' || c == '-' || c=='\\');
// c = '#';
return flg;
}
double gravity() {
double last = w / 2.0;
double mid = w / 2.0;
double res = last;
double sum = 0;
int weight = 0;
for (int i = 0; i < h; ++i) {
for (int j = 0; j < w; ++j) {
if (isBlock(graph[i][j])) {
sum += j + 0.5;
++weight;
}
}
}
if (weight != 0)
sum /= weight;
else sum = mid;
return sum;
}
int cmp(double d, int i) {
}
int main() {
scanf("%d%d", &h, &w);
getchar();
for (int i = 0; i < h; ++i) {
scanf("%s", graph[i]);
}
for (int j = 0; graph[h - 1][j]; ++j) {
if (isBlock(graph[h - 1][j])) {
leftMost = min(leftMost, j);
rightMost = max(rightMost, j);
}
}
double gra = gravity();
// cout << gra << endl;
// cout << leftMost << " " << rightMost << endl;
if (gra < leftMost - eps) {
puts("left");
} else if (gra > rightMost + 1 + eps) {
puts("right");
} else puts("balanced");
return 0;
}
Isomorphic Inversion
Problem Description
Let s be a given string of up to 106 digits. Find the maximal k for which it is possible to partition s into k consecutive contiguous substrings, such that the k parts form a palindrome. More precisely, we say that strings s0, s1, . . . , sk−1 form a palindrome if si = sk−1−i for all 0 ≤ i < k.
In the first sample case, we can split the string 652526 into 4 parts as 6|52|52|6, and these parts together form a palindrome. It turns out that it is impossible to split this input into more than 4 parts while still making sure the parts form a palindrome.
Input
• A nonempty string of up to 10^610
6
digits.
Output
• Print the maximal value of k on a single line.
Sample Input
652526
Sample Output
4
Sample Input2
12121131221
Sample Output2
7
Sample Input3
123456789
Sample Output3
1
Sample Input4
132594414896459441321
Sample Output4
9
Solution
从字符串两端开始枚举,利用hash即可
上午才做了一道hash 结果下午训练还把hash写错。。。 最后没做出来 赛后才检查出bug。。。
队友写的一边枚举一边计算hash时间上比我快了一倍 下面这代码是先与计算hash的
AC Code
#include