偶然间看到一篇《基于加权马尔可夫模型在彩票预测中的应用》的论文,本着学习的精神对其中提到的算法进行了实现,并将该算法应用到双色球蓝球的预测中,此文仅记录学习过程。
一、什么是马尔可夫链模型
简单的说马尔可夫链描述的是一类随机过程,在该过程中将来发生事件的概率仅与当前状态相关,而与过去状态无关,称为“无后效应”。举例来说,考虑池塘里面的青蛙在不同的荷叶上面跳动,假设青蛙无记忆力,则青蛙下一跳跳往每个荷叶的概率只与当前荷叶相关,而与之前所在荷叶无关。在此假设下,彩票的出奖规律亦可看成是一个马尔可夫模型,即下一期出奖结果只与当前期结果相关。
二、马尔可夫链模型的基本概念
1.状态空间。类似于池塘中的荷叶,每个荷叶上面是否有青蛙构成了状态空间,假设有共有5个荷叶,那么[0,1,0,0,0]来表示青蛙当前处于2号荷叶上的状态,总共5个状态便可描述出该池塘中青蛙所处的任意状态。
2.状态转移概率矩阵。青蛙从i荷叶跳往j荷叶的概率,(i,j属于1-5)
3.C-K公式。该公式证明,满足马尔可夫链模型的随机过程可以根据一步状态转移矩阵P,其n步状态转移矩阵为P的n次幂,即初始状态经过n次状态转移后的预测结果可以由初始状态乘P的n次幂。
3.自相关系数,时滞权重。由于仅根据当前状态预测下一状态,利用的信息有限,根据C-K公式,可以增加往期数据来同时预测下一期结果。具体到彩票中来将就是,本期状态乘1次状态转移概率矩阵P得到一个预测结果,利用上1期结果乘P的2次方预测一次结果,依次使用上10期结果分别预测10次结果。但这些结果对下一期结果占的比重不同,此时就需要计算自相关系数,通过自相关系数计算出时滞权重,即为前k期结果对下一期结果的影响权重。
三、算法计算结果
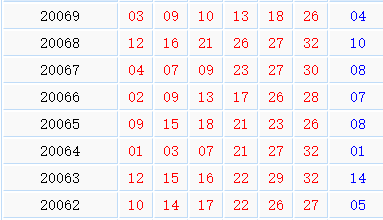
本次以双色球20069期往前100期数据为基础,以蓝球16个号为状态空间
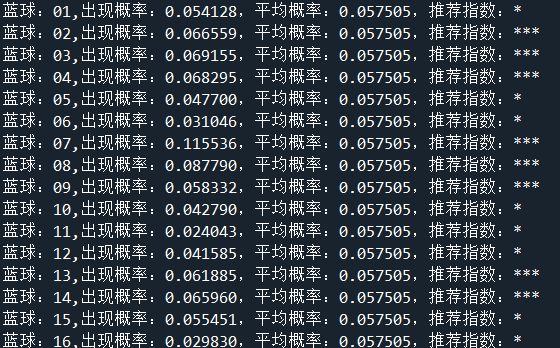
经过计算出,预测20070期蓝球的预测结果如下:
由图可见,2,3,4,7,8,9,12,13的概率较大,其中7号最大。
嗯,整个实现下来对马尔可夫链的模型有了比较深入的理解,但是目前还不敢保证预测的准确性。
下一步打算,在马尔可夫计算的之后,使用BP神经网络来学习各步对预测结果的影响权重,应该可以提高一点准确性。
补充:将数据范围扩大到从18001-20069后,得出结果为:
蓝球:01,出现概率:0.077902,平均概率:0.061213,推荐指数:***
蓝球:02,出现概率:0.056231,平均概率:0.061213,推荐指数:*
蓝球:03,出现概率:0.073559,平均概率:0.061213,推荐指数:***
蓝球:04,出现概率:0.063074,平均概率:0.061213,推荐指数:***
蓝球:05,出现概率:0.050208,平均概率:0.061213,推荐指数:*
蓝球:06,出现概率:0.053989,平均概率:0.061213,推荐指数:*
蓝球:07,出现概率:0.081131,平均概率:0.061213,推荐指数:***
蓝球:08,出现概率:0.048796,平均概率:0.061213,推荐指数:*
蓝球:09,出现概率:0.057353,平均概率:0.061213,推荐指数:*
蓝球:10,出现概率:0.053677,平均概率:0.061213,推荐指数:*
蓝球:11,出现概率:0.067261,平均概率:0.061213,推荐指数:***
蓝球:12,出现概率:0.061003,平均概率:0.061213,推荐指数:*
蓝球:13,出现概率:0.052646,平均概率:0.061213,推荐指数:*
蓝球:14,出现概率:0.064334,平均概率:0.061213,推荐指数:***
蓝球:15,出现概率:0.054940,平均概率:0.061213,推荐指数:*
蓝球:16,出现概率:0.063298,平均概率:0.061213,推荐指数:***
有兴趣的同学加微信:zyw1123888,共同研究进步