R语言与Markov Chain Monte Carlo(MCMC)方法学习笔记(2)

   前面已经大致的叙述了MCMC方法。今天来分享一下R中的一个实现MCMC算法的包mcmc。

   mcmc包的一个核心函数就是metrop，其调用格式为：

metrop(obj, initial, nbatch, blen = 1, nspac = 1, scale = 1, outfun,
    debug = FALSE, ...)

   参数介绍：

obj:这里可以是一个metropo生成的对象，也可以是后验分布的对数似然函数

initial:初始值

nbatch:需要进行迭代的次数

blen：需要每批模拟的长度

   这里metropo函数采用的模拟办法是正态随机游走，如果你要用其他办法去做，至少mcmc包没法帮你实现。

   我们来看一个生成正态分布的例子：

h<-function(x){log(dnorm(x))}
out <- metrop(h, 0, 5000)

   我们得到的模拟结果在out对象的batch中，除此之外，out还还包含了如下对象：

> names(out)
 [1] "accept"       "batch"        "initial"      "final"       
 [5] "initial.seed" "final.seed"   "time"         "lud"         
 [9] "nbatch"       "blen"         "nspac"        "scale"       
[13] "debug" 

   其中accept表示转移接受的概率，我们在之前的讨论就说过，一般accept要控制在40%左右为最佳，太大或太小对数据自相关性影响都比较大，过大或过小可以通过调整metropo中的scale参数得到改善。lud显示我们设置的对数似然。batch储存模拟结果。

  在本例中，我们可以看到：

> out$accept
[1] 0.699

  是一个大致可以接受的结果。

  运行acf(out$batch)我们可以来看看数据的自相关：

  我们可以每隔15个点进行一次采样，将得到的数据进行ks检验，我们可以看到：

> a<-out$batch[seq(1000,5000,by=15),]
> ks.test(a,pnorm)
        One-sample Kolmogorov-Smirnov test
data:  a
D = 0.0525, p-value = 0.4524
alternative hypothesis: two-sided

  可以认为模拟是成功的。

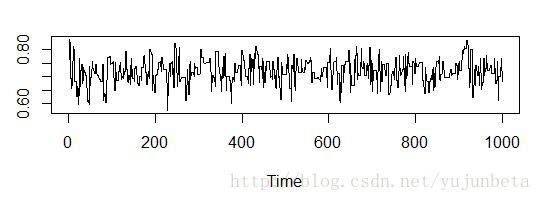
  我们可以得到诊断常用的径迹图：

plot(ts(out$batch))

  这里我们不在披露运行结果，从图中我们可以看到运行结果良好，混合充分。

  我们这里再介绍一个mcmc的例子，来说明函数的使用。

  例子：（混合分布的估计）假设Y服从混合正态分布Y~x*norm(y,7,0.5) + (1-x)*norm(y,10,0.5)。我们要对参数x进行估计。

  我们运行下列代码可以得到Y的模拟数据：

y.sim<-NULL
for(i in 1:100){
	x1<-rnorm(1,7,0.5)
	x2<-rnorm(1,10,0.5)
    d<-rbinom(1,1,0.7)
    y.sim[i]<-x1*d+x2*(1-d)
}

    我们将y.sim赋值给数据集y。（之前没有说明这一点，感谢网友@ blbailei 指正）

    接下来，我们使用mcmc办法得到x的估计：

f<-function(x,y){if(all(x>=0&&x<=1)) 
return(log(prod(x*dnorm(y,7,0.5) + (1-x)*dnorm(y,10,0.5))))
else return(-Inf)}
out <- metrop(f, 0.5, 1000,y=y)

  我们看accept的时候会发现，accept为0.062（可能由于随机种子的不同，答案有差异）。于是修改scale参数：

out <- metrop(out,y=y, scale = 0.1)

  可以看到accept变为0.453。认为这次模拟大致是可行的。我们先来看诊断图（运行plot(ts(out$batch))）：

   可以看出效果良好，我们对x的估计就是x的均值，本例中：

> mean(out$batch)
[1] 0.7197006

  与真值0.7十分接近，进一步，我们可以计算估计量的方差。

  回顾一下metrop() 中的参数nbatch，与它对应的还有一个参数是blen；nbatch 是要模拟的批数，blen 是要模拟的每批的长度，blen 默认为1。假如nbatch=100，blen=100，那么马氏链共转移100*100=10000 次.

  

  从自相关来看，blen选5就不错了，撑死了选10.我们选10为例，运行下列代码：

out <- metrop(out, nbatch = 100, blen = 10, outfun = function(z, ...) c(z,
z^2),y = y)

  接受概率约为 0.456，是不错的。outfun 函数的作用是方便构建一些统计量。对于这个问题，我们关心的是后验均值和方差。均值的计算相对简单，只需要对涉及的变量进行平均。但是方差的计算有点棘手。我们需要利用等式

var(X) = E(X^2)-E(X)^2

将方差表示为可以通过简单的平均进行估计的两部分的方程。因此，我们只需要得到样本的一阶矩和二阶矩。此处，函数outfun 可针对参数(状态向量)z 返回c(z, z^2)。function() c(z, z^2)的含义是，每次马氏链转移取样时，得到的一个状态x, 把这个状态带入函数中，得到状态本身值，以及它的平方值。这样我们可以求解样本一阶距及二阶矩。

  运行下列代码：

foo <- apply(out$batch, 2, mean)
foo
sigmasq<- foo[2] - foo[1]^2

  估计值为：x的估计值：0.7153474，估计量的方差：0.001771402，蒙特卡洛误差：0.002627232。

  从数据上来看这是一个不错的估计，不是么？

  从上面来看，我们的mcmc包还是很好用的，如果需要一个多元的估计，mcmc包的demo文档提供了一个很好的例子（Charles J. Geyer的MCMC Package Example (Version 0.9-2)），有兴趣的同学可以自己去找来看看。它的案例是logistic回归的系数估计。

  最后，以Charles J. Geyer的An MCMC Package for R中的一段话作为本文的结尾：This package is a simple rst attempt at a sensible general MCMC package.It doesn't do much yet. Itonly does normal random-walk" Metropolis for continuous distributions.No non-normal proposals.No Metropolis-Hastings or Metropolis-Hastings-Green.No discrete state.No dimension jumping. No simulated tempering.No perfect sampling. 换句话说，there still a lot to cover，也希望读者能够推荐更好用的MCMC的package给我。

本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。