算法入门刷题笔记 2020北京理工大学ACM冬训课堂笔记：第九讲 - DFS&BFS&图 && A - Fixing Banners - J - Cyclic Component

写在前面

好久没更新公众号和博客了，因为最近在研究新的方向，所以很少发文。
笔者接触编程只有一年，这一年间主要研究启发式算法在运筹学中的应用。但是由于编程基础薄弱，在进一步研究复杂运筹学问题时发现基础算法不过关导致写出的代码运行速度很慢，因此很苦恼。所以决定这个暑假补习一下基础算法，主要是刷一些简单的ACM入门题。偶尔会发一些刷题笔记（偶尔！）。和作者有类似目标的同学可以一起交流共勉！

目前在看的教程：
北京理工大学ACM冬季培训课程

算法竞赛入门经典/刘汝佳编著．－2版可以在这里下载->github

课程刷题点
Virtual Judge

刷题代码都会放在github上，欢迎一起学习进步！

昨天不是没刷，是懒得写博客了，今天一并记上。这期笔记可能比较杂，作者是看了紫书第六章后再跳到着讲看的，大家可以先看下我博客里关于紫书第六讲的内容。

P9 - DFS&BFS&图

next_permutation()函数可以生成下一个全排列，并判断是否已经生成n!个全排列。（需要定义＜）

DFS求全排序时间复杂度O(n!)

集合的枚举：选或不选。

复杂度O(2^n)

位运算处理集合速度非常快

数独与剪枝：

V1.0：所有位置填满1~9的数字，类似全排列。

V2.0：可行性剪枝：每填入一个数字check一次。所有空位置上填合法数字，填满即为答案。

V3.0：搜索顺序剪枝：在所有位置中，总是选择合法数字最少的位置来填。（对搜索可行解的题目）

剪枝没有改变复杂度。

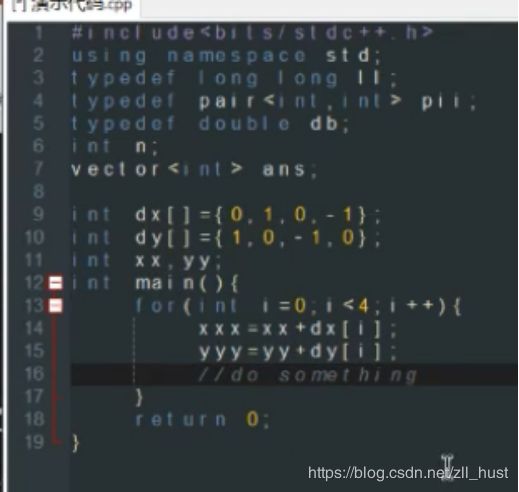
枚举一个点周围四个点：利用数组高效实现

八连块问题，用dfs做比较简单，紫书U6中有过。

迷宫问题：

图：

输出的一些操作：

pair+vector实现邻接表存储带权图

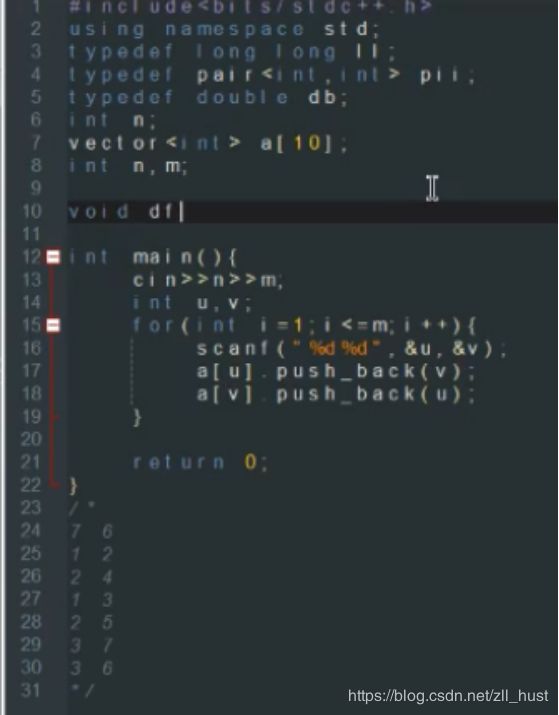
存图：

DFS遍历：

BFS遍历，顺便找到某起点最短路距离（dis数组）：

刷题点;

bfs和dfs难度不大~

L题和之后难度很大，不用强求。

下面是习题部分。

A - Fixing Banners

有6串字符串，问能否从每串中截取一个字符，构成harbin。

咋看是遍历字符串的问题，但是每个字符串长度有$2\ast 10^6$之多，直接遍历就是$12\ast 10^6$，达到了$10^7$次级，可能会TLE。结合这讲的主题DFS，可能是考虑用DFS做。

每次dfs搜索第k个字符串，找到harbin中某个未搜索到的字母，则进入下一个字符串，若找不到，返回false。

以前不知道，做过这个专题才发现dfs、bfs有好多妙用，适用范围很广。不过bfshedfsnandubuda也是真的（doge）。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
#define LOCAL

string banners[10];
char ki[6] = {'h', 'a', 'r', 'b', 'i', 'n'};
int vis[6];

bool dfs(int ban)
{
    // 边界判断
    bool flag = true;
    for(auto exist: vis)
        if(!exist)
        {
            flag = false;
            break;
        }
    if(flag) 
        return true;

    for(int i = 0; i < banners[ban].size(); i++)
    {
        for(int j = 0; j < 6; j++)
            if (banners[ban][i] == ki[j])
            {
                vis[j] = 1;
                if(dfs(ban + 1))
                    return true;
                else
                {
                    vis[j] = 0;
                    break;
                }
            }
    }
    return false;
}



int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    int n;
    cin >> n;
    while(n--){
        for(int i = 0; i < 6; i++)
            cin >> banners[i];
        memset(vis, 0, sizeof(vis));
        if(dfs(0))
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }
    return 0;
}

B - Rescue

走迷宫，迷宫中路径的权值可以是1或2。

这题气死我了。昨天半夜做，做出来的答案我搞错删了，还瞎改了好久。气。就拿了一份别人的来，反正写的和我差不多。

走迷宫一般用BFS。因为路径权值不一样，要搞一个优先队列，就能保证第一个到达目的地的路径最短。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
// #define LOCAL

int n, m;
char graph[205][205];
int sx, sy, ex, ey;
int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
struct node
{
    int x, y, step;
    friend bool operator<(node a, node b)
    {
        return a.step > b.step;
    }
} a, temp;
int bfs()
{
    a.x = sx;
    a.y = sy;
    a.step = 0; //初始化从'r'开始走的位置
    priority_queue<node> q;
    q.push(a); //入栈
    while (!q.empty())
    {
        a = q.top(); //取栈顶赋予a
        q.pop();
        if (a.x == ex && a.y == ey)
            return a.step; //判断是否遇到了'a'
        for (int i = 0; i < 4; i++) //进行探索上下左右
        {
            temp.x = a.x + dir[i][0];
            temp.y = a.y + dir[i][1];
            if (temp.x < n && temp.x >= 0 && temp.y < m && temp.y >= 0 && graph[temp.x][temp.y] != '#') //判断是否能走
            {
                if (graph[temp.x][temp.y] == '.' || graph[temp.x][temp.y] == 'a')
                    temp.step = a.step + 1;
                else
                    temp.step = a.step + 2;
                graph[temp.x][temp.y] = '#';
                q.push(temp);
            }
        }
    }
    return 0;
}
int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    int ans;
    while (scanf("%d%d", &n, &m) != EOF)
    {
        for (int i = 0; i < n; i++)
            scanf("%s", graph[i]);
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {
                if (graph[i][j] == 'r')
                {
                    sx = i;
                    sy = j;
                }
                if (graph[i][j] == 'a')
                {
                    ex = i;
                    ey = j;
                }
            }
        }
        ans = bfs();
        if (ans)
            printf("%d\n", ans);
        else
            printf("Poor ANGEL has to stay in the prison all his life.\n");
    }
    return 0;
}

C - Prime Ring Problem

特地查了一下AK是啥意思，不得不说信息竞赛大佬们骚话真的多，相比之下物竞数竞真的太淳朴了。

DFS。order[]数组存放顺序，m == 1 || isPrime(order[m - 1] + order[m])则dfs(m+1)。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
// #define LOCAL

int n;
int vis[25];
int order[25];

bool isPrime(int n)
{
    for (int i = 2; i <= sqrt(n); i++)
    {
        if ((n % i) == 0)
            return false;
    }
    return true;
}

void dfs(int m)
{
    // for (int i = 1; i <= m - 1; i++)
    //     printf("%d ", order[i]);
    // cout << endl;
    if ((n + 1) == m && isPrime(order[1] + order[n]))
    {
        for (int i = 1; i <= n; i++)
            printf("%d ", order[i]);
        cout << endl;
        return;
    }

    for (int i = 1; i <= n; i++)
    {
        if (!vis[i])
        {
            vis[i] = 1;
            order[m] = i;
            if (m == 1 || isPrime(order[m - 1] + order[m]))
                dfs(m + 1);
            vis[i] = 0;
        }
    }
}

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    int kase = 0;
    while (cin >> n)
    {
        if(kase)
            cout << endl;
        printf("Case %d:\n", ++kase);
        memset(vis, 0, sizeof(vis));
        memset(order, 0, sizeof(order));
        order[1] = 1;
        vis[1] = 1;
        dfs(2);
    }
    return 0;
}

D - Lake Counting

前两天紫书刚做过。改一下字符即可AC。DFS。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
// #define LOCAL

void swap(int &x, int &y)
{
    int temp = x;
    x = y;
    y = temp;
}

const int maxn = 100 + 5;
char pic[maxn][maxn];
int m, n;
int idx[maxn][maxn]; //idx标记是否访问过

void dfs(int r, int c, int id)
{
    if (r < 0 || r >= m || c < 0 || c >= n)
        return; //"出界"的格子
    if (idx[r][c] > 0 || pic[r][c] != 'W')
        return;     //不是"@"或者已经访问过的格子
    idx[r][c] = id; //连通分量编号 (其实标记为1就够了)
    for (int dr = -1; dr <= 1; dr++)
        for (int dc = -1; dc <= 1; dc++)
            if (dr != 0 || dc != 0)
                dfs(r + dr, c + dc, id);
}

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    while (scanf("%d%d", &m, &n) == 2 && m && n)
    {
        for (int i = 0; i < m; i++)
            scanf("%s", pic[i]);
        memset(idx, 0, sizeof(idx));
        int cnt = 0;
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                if (idx[i][j] == 0 && pic[i][j] == 'W')
                    dfs(i, j, ++cnt);
        printf("%d\n", cnt);
    }
    return 0;
}

F - Smallest Difference

第一步全排列，第二步从中间切割。这题应该是考第一张图里的next_permutation函数应用。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
// #include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
// #define LOCAL

void swap(int &x, int &y)
{
    int temp = x;
    x = y;
    y = temp;
}

int num[1005];
int n, len;
int ans;

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    int n;
    cin >> n;
    cin.get();
    while (n--)
    {
        len = 0;
        string str;
        getline(cin, str);
        stringstream ss(str);
        while(ss >> num[len]) 
            len++;

        if (len == 2) //就两个数
        {
            cout << abs(num[0] - num[1]) << endl;
            continue;
        }

        int n1, n2;
        ans = INT_MAX;
        int mid = len / 2;
        do
        {
            n1 = num[0], n2 = num[mid];
            if (n1 == 0 || n2 == 0)
                continue;
            for (int i = 1; i < mid; i++)
                n1 = n1 * 10 + num[i];
            for (int i = mid + 1; i < len; i++)
                n2 = n2 * 10 + num[i];
            ans = min(ans, abs(n1 - n2));
        } while (next_permutation(num, num + len)); //全排列
        cout << ans << endl;
    }

    return 0;
}

G - Divide by three, multiply by two

严重怀疑泰泰学长是真人被黑。

专题有注释，这题用来练习一般图里的DFS。所以我还是用的DFS，但是没用到图。现在明白了，大概是要用数字表示点，邻接表表示图， 因为只有两条边。不过后面有一题用的邻接表DFS，算是补回来了。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
// #define LOCAL

int n;
int vis[25];
int order[105];
ll num[105];

bool dfs(int cur, int m)
{
	if (n == m)
	{
		for (int i = 0; i < n; i++)
			printf("%d ", num[order[i]]);
		cout << endl;
		return true;
	}

	ll x1 = num[cur] * 2, x2 = 0;
	if (num[cur] % 3 == 0)
		x2 = num[cur] / 3;

	for (int i = 0; i < n; i++)
	{
		if (!vis[i])
		{
			if (num[i] == x1 || (x2 && num[i] == x2))
			{
				vis[i] = 1;
				order[m] = i;
				if (dfs(i, m + 1))
					return true;
				vis[i] = 0;
			}
		}
	}
	// cout << "sorry, not find!" << endl;
	return false;
}

int main()
{
#ifdef LOCAL
	freopen("data.in", "r", stdin);
	// freopen("data.out", "w", stdout);
#endif
	cin >> n;
	for (int i = 0; i < n; i++)
		cin >> num[i];
	memset(vis, 0, sizeof(vis));
	memset(order, 0, sizeof(order));
	for (int i = 0; i < n; i++)
	{
		vis[i] = 1;
		order[0] = i;
		dfs(i, 1);
		vis[i] = 0;
	}
	return 0;
}

I - Nearest Opposite Parity

给一个数组$a[i]$，对每一个位于i的点，有一条边连向$i-a[i](if1\le i-a[i])或i+a[i](ifi+a[i]\le n)$的边。那么用BFS找最短路就ok了。

这里要用邻接表表示图，不然容量很可能超，因为有$2\ast 10^5$个数字。（我不会告诉你们虽然我用了邻接表容量也超了的）

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
// #define LOCAL

int n;
vector<int> arc[200005];
int a[200005];

int bfs(int m)
{
	queue<pii> q;
	q.push({ m, 0 });
	while (!q.empty())
	{
		pii now = q.front();
		q.pop();
		if (now.first != m && (a[now.first] % 2 != a[m] % 2))
			return now.second;
		for (auto to : arc[now.first])
		{
			q.push({ to, now.second + 1 });
		}
	}

	return -1;
}
int main()
{
#ifdef LOCAL
	freopen("data.in", "r", stdin);
	// freopen("data.out", "w", stdout);
#endif
	int ans;
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
		arc[i].clear();
		if ((i - a[i]) > 0 && (i - a[i]) <= n)
			arc[i].push_back(i - a[i]);
		if ((i + a[i]) > 0 && (i + a[i]) <= n)
			arc[i].push_back(i + a[i]);
	}

	for (int i = 1; i <= n; i++)
	{
		ans = bfs(i);
		printf("%d ", ans);
	}

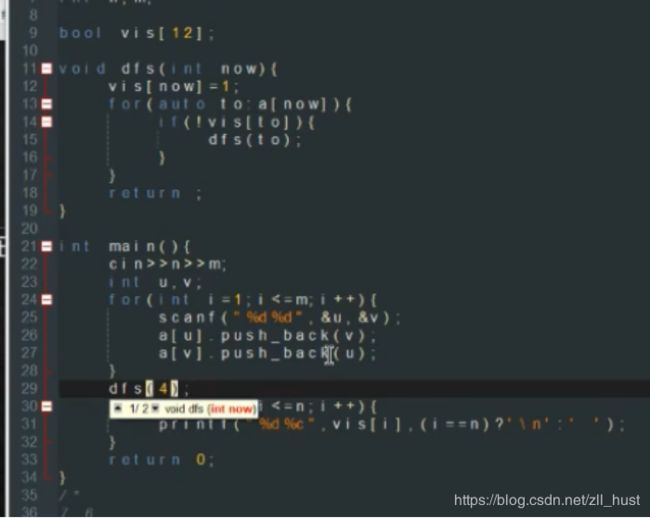
	return 0;
}

J - Cyclic Components

注意这里的环和connected component连接通量不一样，这里说的是换，且环中除了环内的边外没有其他边。所以每个点的边只有两条。

明显用DFS。一个重要的判断条件是边是否有两条。为了方便终止条件判定，我在dfs传参时加入了pre，最后一个点找不是pre的边（记住只有两条边），判断是否已访问，若访问则为环。这里不能简单用vis数组标记，这样会直接跳过，无法判断终止。

两条边，用邻接表。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
#define LOCAL

int n, m;
int ct;
vector<int> arc[105];
int vis[100];

bool dfs(int now, int pre)
{
	vis[now] = 1;
	if (arc[now].size() != 2)
		return false;
	int fg = 0;
	for (auto to : arc[now])
	{
		if(to == pre)
			continue;
		if (!vis[to])
		{
			if (dfs(to, now))
				return true;
			else
				return false;
		}
		else if (vis[to] && arc[to].size() == 2)
			return true;
	}
	return false;
}

int main()
{
#ifdef LOCAL
	freopen("data.in", "r", stdin);
	// freopen("data.out", "w", stdout);
#endif
	int ct = 0;
	scanf("%d %d", &n, &m);
	memset(vis, 0, sizeof(vis));
	for (int i = 0; i < m; i++)
	{
		int u, v;
		scanf("%d%d", &u, &v);
		arc[u].push_back(v);
		arc[v].push_back(u);
	}

	ct = 0;
	for (int i = 1; i <= n; i++)
	{
		if (!vis[i])
		{
			if (dfs(i, -1))
				ct++;
		}
	}
	printf("%d\n", ct);

	return 0;
}

刷到这里可能会有同学注意到我跳了H和E，因为看Overview就知道很麻烦…看了下H，确实不太会，AC的答案又都没share，就很难受…所以这个专题我就刷到这里了。