算法入门刷题笔记 2020北京理工大学ACM冬训课堂笔记：第十讲 - 拓扑排序&最短路 & Day5 贪心 A - FatMouse‘ Trade - F - Parallelogram is Bac

写在前面

好久没更新公众号和博客了，因为最近在研究新的方向，所以很少发文。
笔者接触编程只有一年，这一年间主要研究启发式算法在运筹学中的应用。但是由于编程基础薄弱，在进一步研究复杂运筹学问题时发现基础算法不过关导致写出的代码运行速度很慢，因此很苦恼。所以决定这个暑假补习一下基础算法，主要是刷一些简单的ACM入门题。偶尔会发一些刷题笔记（偶尔！）。和作者有类似目标的同学可以一起交流共勉！

目前在看的教程：
北京理工大学ACM冬季培训课程

算法竞赛入门经典/刘汝佳编著．－2版可以在这里下载->github

课程刷题点
Virtual Judge

刷题代码都会放在github上，欢迎一起学习进步！

今天看了第九讲和第四、五讲。四和五讲的不太好，没做笔记。然后题目先做的贪心，因为想换换口味。

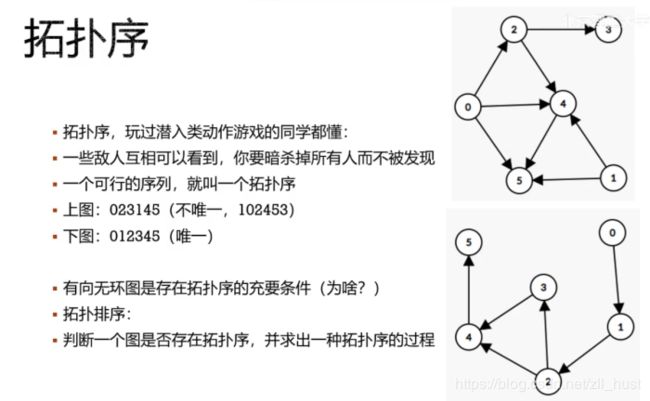
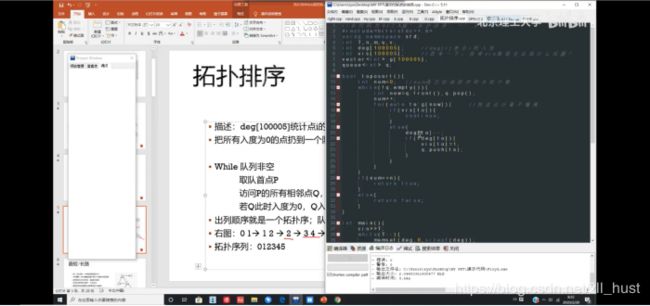
拓扑排序

有向无环图：DAG。（有一条双向边也相当于有环）

概念

基本步骤

具体操作

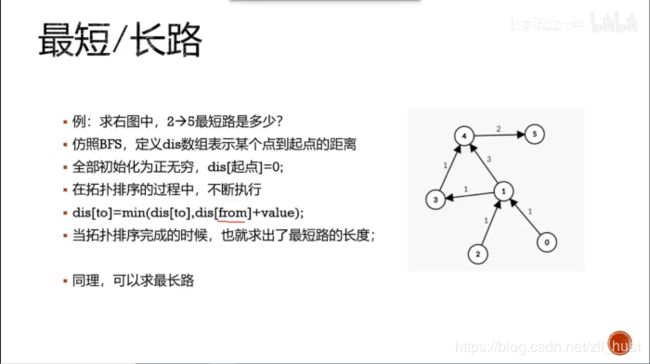
最短路/最长路

动态规划实际上是在一张有向无环图上进行拓扑排序的过程。

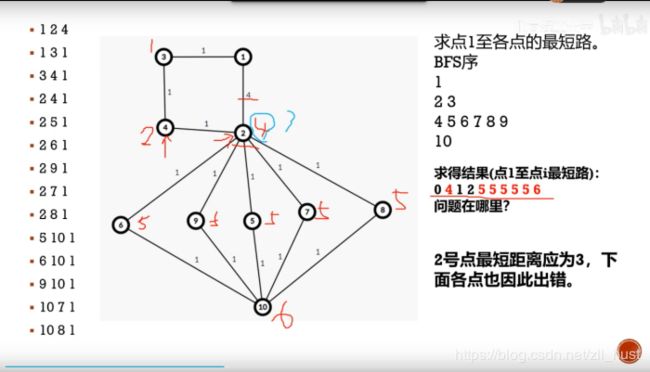
最短路

BFS

一般BFS求最短路要求边的权重相同。

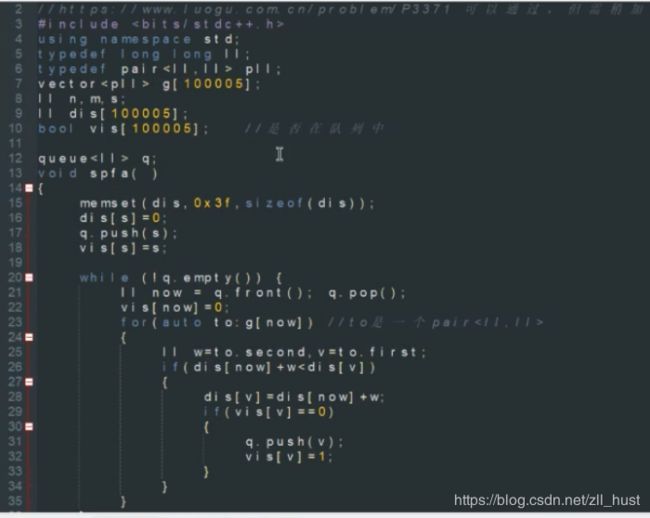
SPFA

著名笑话：

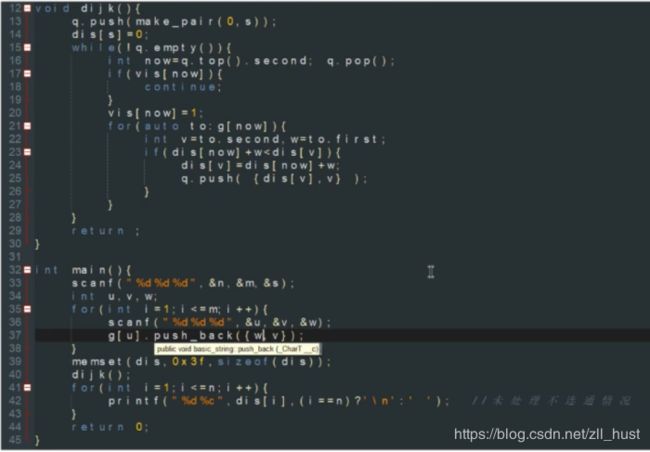
Dijkstra

用了pair自定义的排序，所以第一位为距离。

准确的说这是堆优化下的dijkstra，普通的遍历找最短距离最近的点。

Bellman-ford

SPFA是队列优化的Bellman，一般不会用到bellman。

（话说图里的式子是不是搞反了）

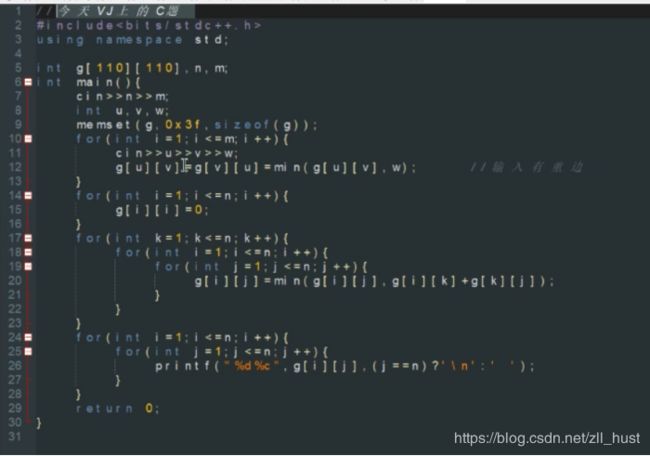
Floyd

总结

tip

题目

下面开始贪心部分习题。

刷题点：https://vjudge.net/contest/356986

密码：greedy

A - FatMouse’ Trade

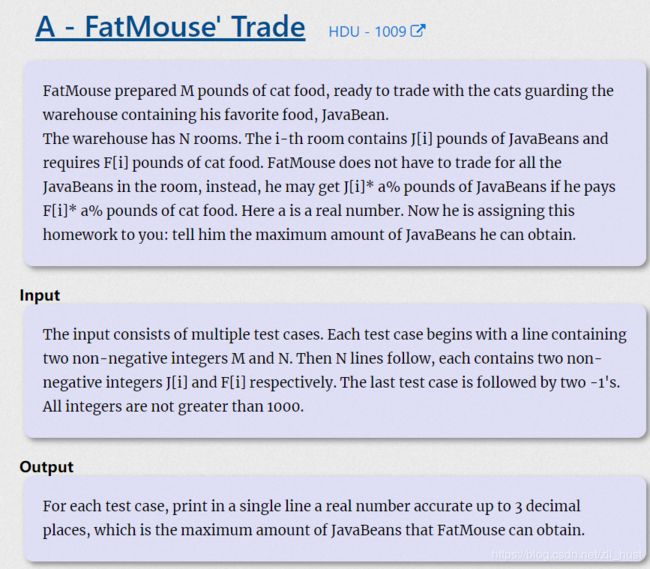
给n个物品，物品价值有高有低，问怎么购买能用有限的前买到价值最高的物品。

纯贪心。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, int> pdi;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
#define LOCAL

const int maxn = 1000 + 5;
int J[maxn];
int F[maxn];
pdi deg[maxn];

int main()
{
#ifdef LOCAL
	freopen("data.in", "r", stdin);
	// freopen("data.out", "w", stdout);
#endif
	int m, n;
	while (cin >> m >> n && m != -1)
	{
		for(int i = 0; i < n; i++)
		{
			cin >> J[i] >> F[i];
			deg[i] = {(double)J[i] / (double)F[i], i};
		}
		sort(deg, deg + n);
		reverse(deg, deg + n);
		int cnt = 0;
		double sum = 0;
		while(m)
		{
			if(m >= F[deg[cnt].second])
			{
				sum += J[deg[cnt].second];
				m -= F[deg[cnt].second];
				cnt++;
			}
			else
			{
				sum += deg[cnt].first * m;
				break;
			}
		}
		printf("%.3lf\n", sum);
	}
	return 0;
}

B - Moving Tables

移桌子，有n对桌子要移动，n对桌子的摆放方式如图所示，一次可以移动多对桌子，时间花费固定为10，走廊同时不允许两张并排走。问移动完需要多少时间。

贪心，桌子移动抽象为一个区间，尽可能放置多个区间在同一时间段。直接按开始时间排序，在不冲突的情况下贪心插入即可，因为在可行情况下插入任何一段时间都是一样的。

写博客的时候我好像知道自己为什么AC了，大概是因为忘了考虑房间的结构，相邻奇偶数也不能同时搬运…（如1-3和4-5，3和4碰了）。

错误代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, int> pdi;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
// #define LOCAL

void swap(int &x, int &y)
{
    int temp = x;
    x = y;
    y = temp;
}

const int maxn = 300 + 5;

int main()
{
#ifdef LOCAL
	freopen("data.in", "r", stdin);
	// freopen("data.out", "w", stdout);
#endif
	int kase;
	int n;
	cin >> kase;
	while (kase--)
	{
		cin >> n;
		vector<pii > mov;
		for(int i = 0; i < n; i++)
		{
			int a, b;
			cin >> a >> b;
			if (b > a)
				swap(a, b);
			mov.push_back({a, b});
		}
		sort(mov.begin(), mov.end());
		int cnt = 0;
		while(!mov.empty())
		{
			int temp = mov[0].second;
			mov.erase(mov.begin());
			for(vector<pii>::iterator it = mov.begin(); it != mov.end(); it++)
			{
				if((*it).first > temp)
				{
					temp = (*it).second;
					mov.erase(it);
					it--;
				}
			}
			cnt += 10;
		}
		printf("%.d\n", cnt);
	}
	return 0;
}

C - 今年暑假不AC

第一反应是图。合法的开始结束时间连上一条边，边的权为1，0和24为超级源点，求最短路。不过一想贪心应该不会这么麻烦。仔细一想果然，直接按结束时间排序，再贪心插入就好了。（不好解释，自己仔细想想确实没问题）

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, int> pdi;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
// #define LOCAL

void swap(int &x, int &y)
{
	int temp = x;
	x = y;
	y = temp;
}

const int maxn = 100 + 5;
pii cus[maxn];

int main()
{
#ifdef LOCAL
	freopen("data.in", "r", stdin);
	// freopen("data.out", "w", stdout);
#endif
	int n;
	while (scanf("%d", &n) && n)
	{
		for (int i = 0; i < n; i++)
		{
			int a, b;
			cin >> a >> b;
			cus[i].first = b;
			cus[i].second = a;
		}
		sort(cus, cus + n);
		int temp = cus[0].first, sum = 1;
		for (int i = 1; i < n; i++)
		{
			if (cus[i].second >= temp)
			{
				sum++;
				temp = cus[i].first;
			}
		}
		printf("%d\n", sum);
	}
	return 0;
}

D - 卡片游戏

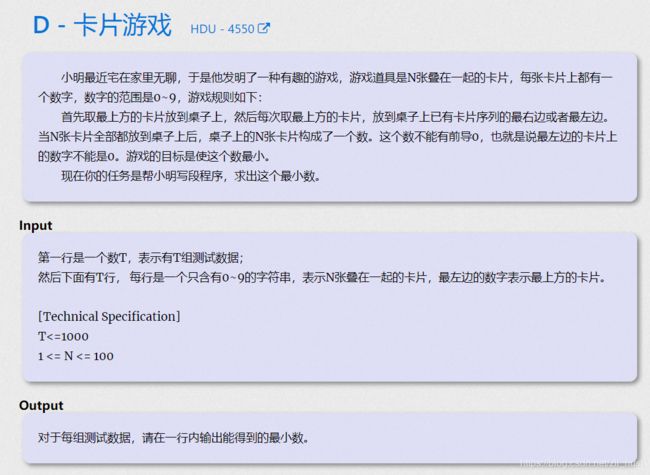
与最左端对比，小则放到左边，大或0则放到右边，相等则和从左数起第二位比较，循环。注意判断下第一个是否为0。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, int> pdi;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
#define LOCAL

void swap(int &x, int &y)
{
	int temp = x;
	x = y;
	y = temp;
}

const int maxn = 100 + 5;

int main()
{
#ifdef LOCAL
	freopen("data.in", "r", stdin);
	// freopen("data.out", "w", stdout);
#endif
	int n;
	cin >> n;
	while (n--)
	{
		string str;
		cin >> str;
		vector<int> num;
		num.push_back(int(str[0]) - '0');
		for (int i = 1; i < str.size(); i++)
		{
			int temp = str[i] - '0';
			for (int j = 0; j < str.size(); j++)
			{
				if(j < (str.size() - 1) && temp == num[j])
					continue;
				else if (!num[j] || (temp < num[j] && temp))
					num.insert(num.begin(), temp);
				else
					num.push_back(temp);
				break;
			}
		}
		int ans = 0;
		for (vector<int>::iterator it = num.begin(); it != num.end(); it++)
			ans = ans * 10 + *it;
		printf("%d\n", ans);
	}
	return 0;
}

E - Bachgold Problem

问一个数最多分解为多少个质数。

奇数则减去一个3，偶数则全为2。想起来我写的时候还用了循环，根本没必要，直接除以2就得了，复杂度O(1)。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, int> pdi;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
// #define LOCAL

void swap(int &x, int &y)
{
	int temp = x;
	x = y;
	y = temp;
}

const int maxn = 100 + 5;

int main()
{
#ifdef LOCAL
	freopen("data.in", "r", stdin);
	// freopen("data.out", "w", stdout);
#endif
	int n;
	cin >> n;
	int n2 = 0, n3 = 0;
	while (n)
	{
		if(n % 2)
		{
			n3++;
			n -= 3;
		}
		else
		{
			n2++;
			n -= 2;
		}
	}
	printf("%d\n", n2 + n3);
	for(int i = 0; i < n2; i++)
		printf("%d ", 2);
	for(int i = 0; i < n3; i++)
		printf("%d ", 3);
	return 0;
}

F - Parallelogram is Back

给三个点，问构成平行四边形的第四个点。

不要太简单…

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, int> pdi;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
// #define LOCAL

void swap(int &x, int &y)
{
	int temp = x;
	x = y;
	y = temp;
}

const int maxn = 100 + 5;

int main()
{
#ifdef LOCAL
	freopen("data.in", "r", stdin);
	// freopen("data.out", "w", stdout);
#endif
	pii node[4];
	for(int i = 0; i < 3; i++)
		cin >> node[i].first >> node[i].second;
	cout << 3 << endl;
	printf("%d %d \n",node[0].first + node[1].first - node[2].first, node[0].second + node[1].second - node[2].second);
	printf("%d %d \n",node[1].first + node[2].first - node[0].first, node[1].second + node[2].second - node[0].second);
	printf("%d %d \n",node[2].first + node[0].first - node[1].first, node[2].second + node[0].second - node[1].second);
	return 0;
}