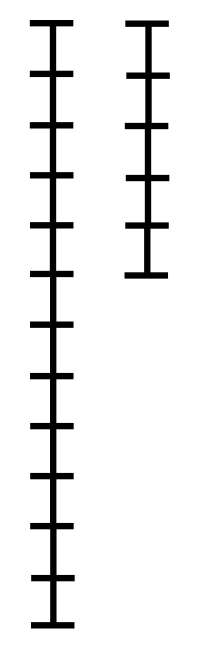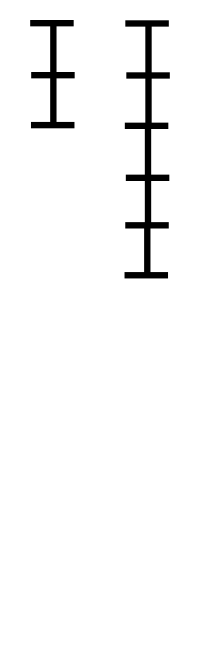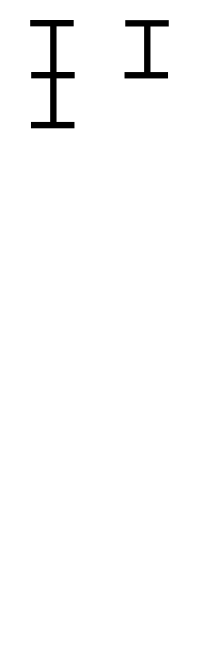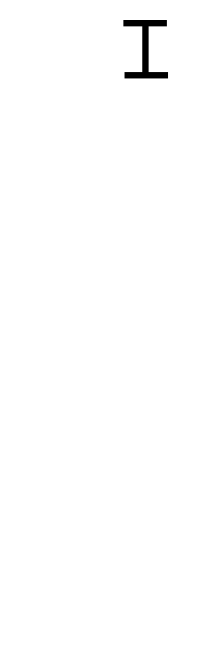简述
给你两个数a和b,要求求出a和b的最大公约数。为了解决这个问题,我们可以想到很多方法,穷举法,辗转相除法,更相减损法等。这里我们详解介绍穷举法和辗转相除法。
问题描述
我们把问题用数学语言进行描述:已知整数a和b,求一数k满足a%k==0&&b%k==0,且k要尽可能大。
穷举法
因为k小于等于a和b,所以我们可以从a和b选一个数开始进行穷举,这里我们选择较小的那个数,因为k一定小于等于较小那个数。
int gcd(int a,int b){ int num=min(a,b); for(int i=num;i>=1;i--){ if(a%i==0&&b%i==0) return i; } }
这个算法的时间复杂度为O(min(a,b)),因为最多会执行min(a,b)次,当a和b特别大的时候,这个程序是很慢的。
辗转相除法
辗转相除法又称欧几里得算法,这是我们小学就学过的算法,古希腊数学家欧几里德在其著作《The Elements》中最早描述了这种算法,所以被命名为欧几里德算法,又在九章算术里描述为辗转相除法。
我们现在将求a和b两个数的最大公约数定义为函数gcd(a,b)。
辗转相除法的算法思想是,gcd(a,b)=gcd(b,a%b),当b为0时gcd(a,b)为a。不断重复gcd(a,b)=gcd(b,a%b)则b终会等于0,最后求出等式的结果。
例如我们现在要求gcd(9,12),则可以写出以下的过程:
gcd(9,12)=gcd(12,9%12)=gcd(12,9)=gcd(9,12%9)=gcd(9,3)=gcd(3,9%3)=gcd(3,0)=3
int gcd(int a,int b){ if(b==0) return a; return gcd(b,a%b); }
辗转相除法的时间复杂度为O(logn),证明省略。
辗转相除法的证明
为什么gcd(a,b)=gcd(b,a%b)呢?
我们设gcd(a,b)=k,r=a%b。
可得a=sk,b=tk,s和t互质,a=bq+r,q为正整数。
左带入右得sk=tkq+r,整理得r=k(s,tq),所以k也是r的因子。
我们可以将求gcd(a,b)的过程理解为求a和b两个因数集合里最大的相同数,将gcd(a,b)=gcd(b,a%b)过程可以理解为使用一个r代替b,使得b变小但r的因数集里包含最大公约数k,一直减小到0时,当时的a就是我们求的k了。
我们开看一张gif图,两条线段的长度分别代表a和b,里面的一小段代表最大公约数,现在演示如何用辗转相除法求最大公约数。