2020牛客暑期多校05 B - Graph 异或最小生成树

20200726005921

2020牛客暑期多校05 B - Graph 异或最小生成树

一、题意

给一棵有 $n$ 个节点的树，第 $i$ 条边有边权 $W_i$。

我们可以无限次地对其增添或删除边，但要求全程始终保证：

1. 图连通；
2. 任意一个环（如果有）上的边的边权的异或和为零；

最后得到一棵新树（也可保持原树不做变动），使得边权之和最少。求边权之和的最小值。

$2\le N\le 10^5;0\le W_i<2^{30};$

二、重要性质：任意两节点之间若连边，则此边的边权确定且不会变化

具体来说，

• 若原树 $u,v$ 之间连边（假设为第 $i$ 条），则边权一定为 $W_i$；
• 若原树 $u,v$ 之间不连边，且它们之间的路径上有边 $\{e_1,...,e_k\}$，则连边时边权为 $(W_{e_1}\oplus ...\oplus W_{e_k})$。

证明：

既然增删过程中，图要连通，那么

• 当前为树时不可继续删边，只可增边；
• 任何一条边删去前一定在某一些（且至少一个）环上，注意这些环上的边的边权的异或和分别为零。

那么，即使某条边（假设为 $e_1$，连在 $u_1,u_2$ 之间，不要求为原树上的边）被删除时，其权值 $W_{e_1}^{\prime }$（作为环上其它边的边权的异或和）仍然被保留了下来。（写作 $W^{\prime }$ 是为了与输入数据变量名作区分）

这条边原来在几个简单环上，删边之后 $u_1,u_2$ 之间就会有几条简单路径（应该没错？？）。每一条路径各自的边的边权异或和都分别为 $W_{e_1}$。

如果这些路径（中的某些）上的某些边又被删去，那么就进一步 “绕远路” ，绕远路涉及的环也还要满足异或和的要求。总之，$u_1,u_2$ 之间任意一条路径上的边的边权异或和都是 $W_{e_1}^{\prime }$。而且，由于 $u_1,u_2$ 之间没有直接连边，为了使全图连通，则 $u_1,u_2$ 之间随时都至少有一条路径。

当这条边想被增加回来时，其权值只能是上述路径的边的边权异或和，因此不变。

因此，任意两点之间若连边，则边权由两点间任意一条当前已有路径的边的边权异或和决定，且任意两点之间任意时刻必然至少有一条路径、这些路径的边权异或和无法改变。

此性质赛上已想出。

三、本题可转化为【异或最小生成树】问题

异或最小生成树问题，是在只给定各点点权值、且各边边权为两端点点权的异或值的完全图上，求最小生成树。

本题可转化为异或最小生成树，或者说，本题可将各边的确定、不变的边权转化为各点点权，是因为

• 可任意指定某一点、赋予任意点权值，然后根据已知边权推得其它点的点权，于是原树上的边满足【边权为两端点点权的异或值】；
• 对于原树上不直接连边的节点 $u_1,u_2$，设原树上路径为 $\{u_1,x_1,...,x_k,u_2\}$，其连边的边权应为 $((u_1\oplus x_1)\oplus (x_1\oplus ...)\oplus ...\oplus (...\oplus x_k)\oplus (x_k\oplus u_2))=(u_1\oplus u_2)$，于是这些边也满足【边权为两端点点权的异或值】。

四、异或最小生成树解法、复杂度证明

（前置知识：字典树）

异或得到所有边权，然后按一般最小生成树问题来做？$O(n^2)$ 条边，不可。

已知权值（点权、边权）小于 $2^{len}$ （本题 $len=30$），则将点权值表示为 $len$ 位二进制数，构造 $len$ 层的字典树。

于是，字典树上的 $n$ 个叶子就表示原图的 $n$ 个节点，我们要在叶子上连 $(n-1)$ 条边使它们互相 “连通”，且生成树边权之和最小。当然，可能存在多个点的点权相同，它们在字典树同一个叶子上、连边时权值为零，当然就要连边，且连了边也不对最小生成树答案的增加做贡献（边权为零），所以直接对点权去重即可。

两叶子 $u_1,u_2$ 连边的边权是它们点权的异或和。在字典树上，假设它们的 LCA （最近公共祖先节点）是 $lca$，则 $u_1,u_2$ 的点权在【从字典树根到 $lca$】表示的所有 bit​ 上都相同，那么在这些 bit 上的异或值当然分别为 $0$。如下图，两点权值 0110000 、 0110101 的异或值为 0000101，则异或值只有第 $[0,3)$ bit 可能为一，高位必都为零。

这些异或和为零的 bit 都在高位上，而我们现在在求最小生成树，自然希望这些高位越低越好，于是就希望 $lca$ 越低越好，于是就希望连边的两点尽量在【层数更小的】子树内。然而，对于同时拥有左右（零/一）儿子的节点（以下简称分叉节点），其左子树中的叶子必然要和右子树中的叶子以它自己为 LCA 相连至少一次，因此我们对于任何一个分叉节点，只以其为LCA连恰好一条边（把左右子树的叶子连通）。

【这一段别看了】至于怎么选边，我们只需分别枚举左右子树上的节点尝试连边，选出其中边权最小者即可。因此，我们对字典树做dfs，在回溯（从低到高）时，对于每个分叉节点按上述方法枚举得到最小边权，连边即可。（这是 https://blog.csdn.net/Galaxy_yr/article/details/102323777 对另一道异或最小生成树题目的做法，似乎还是 $O(n^2)$ 的？）

另一种做法是（ https://blog.csdn.net/tianyizhicheng/article/details/90696847 ），对于字典树每个分叉点，择其两个子树中叶子较少的那个，依次取叶子（点权值）分别在另一子树中直接链状地匹配。例如，分叉点的左子树中叶子较少（只有 $y_L$ 个），我们取其中每个叶子（点权）$x_i$ 时，在右子树中也从分叉点开始向下搜索，对于每个 bit 如果 $x_i$ 上此 bit 的值在右子树此层有对应的节点则进入此节点（于是右子树上选来与 $x_i$ 匹配的叶子，在此 bit 上的异或值为零），否则只好进入另一个节点。如下图，当我们对叶子较少的子树中的某叶子 $x_i=$ ...0110 在另一子树中匹配时，我们尽量在各 bit 匹配同一数字使此 bit 异或值为零，然而在第 $2$ bit 处无法匹配相同值，就只好在此 bit 匹配另一个数字，最终匹配到 ...1100。

这样，对叶子较少的子树中的各叶子分别去另一子树内匹配，能取到各自的最小异或值，最后汇总即可取得此 LCA 处连边时需要的总的最小异或值。

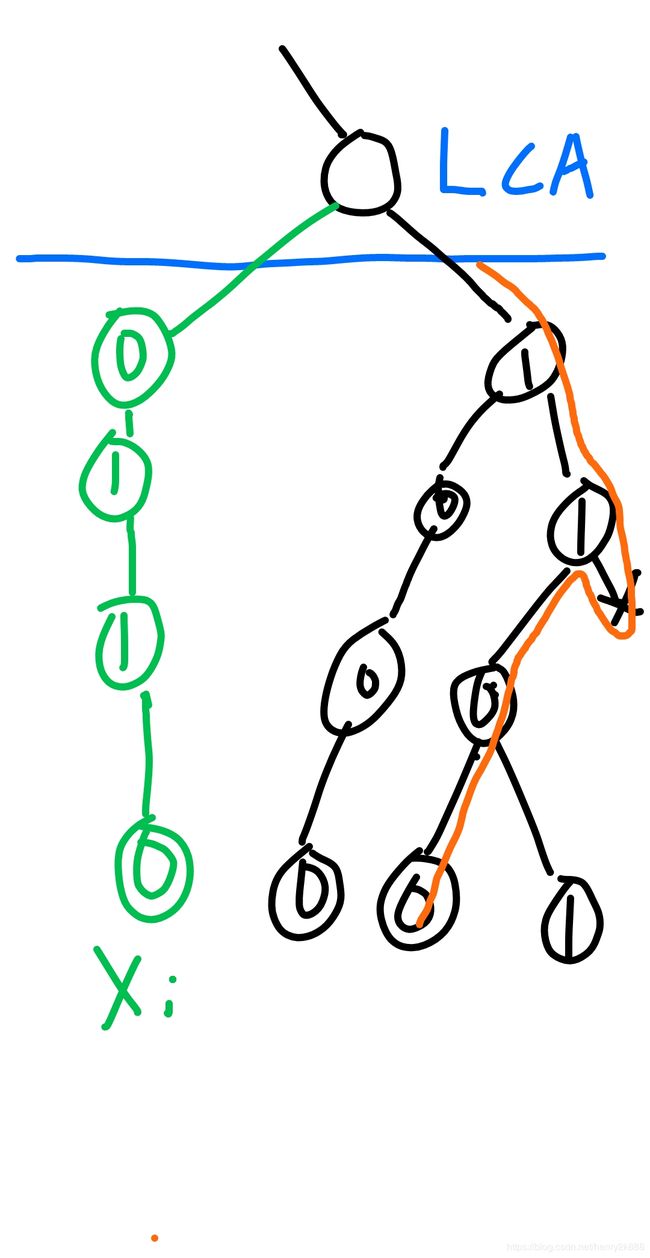
这种做法避免了任意两节点之间异或值的一一比较，优化了时间复杂度。具体来说，设某 LCA 左子树中有 $L$ 个叶子、右子树中有 $R$ 个叶子，则只需比较 $\min (L,R)\le \frac{L+R}{2}$ 次即可从这 $L\cdot R$ 对叶子中选出最小异或值作为此 LCA 担负的连边任务。然后，对每个 LCA，我们根据其与最高 LCA（深度最小的 LCA）之间所隔 LCA 的数量分层，最高 LCA 为 “第零层 LCA”，依此类推。如下图，红色节点为 LCA，我们对其分层。

假设点权去重后剩余 $n^{\prime }$ 个值，则有 $n^{\prime }$ 个叶子。对于第 $i(i\ge 0)$ 层 LCA，设其中第 $j$ 个 LCA 的左子树中有 $L_j$ 个叶子、右子树中有 $R_j$ 个叶子，则此层所有 LCA 造成的叶子比较次数为 ${\sum }_j\min (L_j,R_j)\le {\sum }_j\frac{L_j+R_j}{2}\le \frac{n^{\prime }}{2}$ （第一个小于等于见上一段解释，第二个小于等于可参考上图的第三层 LCA 来理解）。总共最多有 $len$ 层 LCA（一般来说远远达不到），因此总的比较次数为 $O(\frac{len}{2}\cdot n^{\prime })$，其中 $\frac{len}{2}$ 是非常小的常数！如果再算上每次比较过程中沿着树链向下走最多 $len$ 步，则【异或最小生成树】问题复杂度为 $O(\frac{le{n}^2}{2}\cdot n^{\prime })$，其中 $\frac{le{n}^2}{2}$ 也不太大。

实现上还有些技巧：我们可以用最多 $N$ 个 vector（C++）来记录子树中的值，并对字典树维护一个数组 $id[]$ 表示第 $i$ 个（字典树）节点的子树中的叶子所代表的权值们被存储在了第 $id[i]$ 个 vector 中。建字典树（插入单词）时我们只需把（去重后的）每个权值记录在各自叶子所对应的某个 vector 中；在dfs回溯时再向上合并，例如对于字典树节点 $u$，已知当前其左子节点 $L_u$ 和右子节点 $R_u$ 的子树中的叶子分别被存在了第 $id[L_u],id[R_u]$ 个 vector 中，则把其中一个元素较少的 vector 的元素移到另一个 vector 中（完成合并），然后把 $id[u]$ 赋值为 $id[L_u]$ 或 $id[R_u]$ 即可。这样，对于每个 LCA，我们在从较小子树中取值去与另一子树匹配时，取值的步骤就是 $O(1)$ 的了，更重要的是降低了代码编写难度。既然 dfs 过程不仅担负选边任务，还要担负子树叶子集的合并任务，因此各项工作当然是在回溯时进行。

五、AC代码

#include
#include
#include
#include
#define ll long long


// graph

const int fu=0, fv=1, fw=2, fnext=3;
int edge[200005][4];
int edges=0;
int last[100005];

void add_edge(int u , int v , int w){
    edge[edges][fu]=u;
    edge[edges][fv]=v;
    edge[edges][fw]=w;
    edge[edges][fnext] = last[u];
    last[u]=edges;
    ++edges;
}

std::queue<int> que;
int a[100005];


// trie

int trie[3100005][2];
int nodes=1;  // trie root initially exists.
int id[3100005];
std::vector<int> values[100005];

void add_word(int value , int word_id){
    int now=1;
    for(int i=29 ; i>=0 ; --i){
        int bit = ((value>>i)&1);
        if(trie[now][bit]==0) trie[now][bit]=(++nodes);
        now = trie[now][bit];
    }
    id[now] = word_id;
    values[word_id].push_back(value);
}

int matching(int value1 , int now , int depth){
    int xor1 = (1<<(depth-1));  // not value2
    for(int i=depth-2 ; i>=0 ; --i){
        int bit = ((value1>>i)&1);
        if(trie[now][bit]>0){
            now = trie[now][bit];
        }else{
            now = trie[now][1-bit];
            xor1 |= (1<<i);
        }
    }
    return xor1;
}

ll ans;
void dfs(int now , int depth){  // here, depth of leaves are zero!
    if(trie[now][0]>0) dfs(trie[now][0] , depth-1);
    if(trie[now][1]>0) dfs(trie[now][1] , depth-1);
    //printf("\nnow=%d , depth=%d , trie[now][0]=%d , trie[now][1]=%d\n" , now , depth , trie[now][0] , trie[now][1]);
    if(trie[now][0]>0 && trie[now][1]>0){  // now is a LCA
        int min_xor = (1<<30);
        if( values[id[ trie[now][0] ]].size() < values[id[ trie[now][1] ]].size() ){
            for(int i=0 ; i<values[id[ trie[now][0] ]].size() ; ++i){
                int value1 = values[id[ trie[now][0] ]][i];
                int xor1 = matching(value1 , trie[now][1] , depth);
                if(xor1<min_xor) min_xor = xor1;
                //printf("\tvalue1=%d , xor1=%d , min_xor=%d\n" , value1 , xor1 , min_xor);

                values[id[ trie[now][1] ]].push_back(value1);
            }
            id[now] = id[trie[now][1]];
        }else{
            for(int i=0 ; i<values[id[ trie[now][1] ]].size() ; ++i){
                int value1 = values[id[ trie[now][1] ]][i];
                int xor1 = matching(value1 , trie[now][0] , depth);
                if(xor1<min_xor) min_xor = xor1;
                //printf("\tvalue1=%d , xor1=%d , min_xor=%d\n" , value1 , xor1 , min_xor);

                values[id[ trie[now][0] ]].push_back(value1);
            }
            id[now] = id[trie[now][0]];
        }
        ans += min_xor;  // (ll)min_xor ?  // not xor
    }else{
        if(trie[now][0]>0 || trie[now][1]>0) id[now] = id[ trie[now][0] + trie[now][1] ];
    }
}


// main

int main(){
    int N;
    scanf("%d" , &N);

    memset(last , -1 , sizeof last);
    for(int i=1 ; i<N ; ++i){
        int u,v,w;
        scanf("%d%d%d" , &u , &v , &w);
        add_edge(u,v,w);
        add_edge(v,u,w);
    }

    // assign node weight
    memset(a , -1 , sizeof a);
    a[0]=0;
    que.push(0);
    while(! que.empty()){
        int u = que.front(); que.pop();
        for(int e=last[u] ; e>=0 ; e=edge[e][fnext]){
            int v=edge[e][fv];
            if(a[v]>=0) continue;  // not a>=0
            a[v] = (a[u] ^ edge[e][fw]);
            que.push(v);
        }
    }
    std::sort(a , a+N);

    // build trie
    memset(trie , 0 , sizeof trie);
    for(int u=0 ; u<N ; ++u){
        if(u>=1 && a[u]==a[u-1]) continue;  // to ignore duplicates node weight
        add_word(a[u] , u);
        //printf("add word %d : %d\n" , u ,a[u]);
    }
    //for(int u=1 ; u<=nodes ; ++u) printf("u=%d : 0->%d , 1->%d\n" , u , trie[u][0] , trie[u][1]);

    // XOR minimum spanning tree dfs
    ans = 0;
    dfs(1 , 30);
    printf("%lld\n" , ans);

    return 0;
}

六、参考资料

G. Xor-MST 异或边的最小生成树 分治

https://blog.csdn.net/qq_41955236/article/details/90715120

Codeforces Contest 888 G Xor-MST —— 求异或最小生成树

https://blog.csdn.net/tianyizhicheng/article/details/90696847

【重要】

[题解]决斗 异或最小生成树

https://blog.csdn.net/Galaxy_yr/article/details/102323777