玉蟾宫(悬线法)

玉蟾宫(题面)

考虑运用悬线法求最大01子矩阵

• 方法对于每个点 \(i\) 求其,向左 \(l[i][j]\) , 向右 \(r[i][j]\) 能达到的最大位置和向上 \(up[i][j]\) 能达到的最大距离
• 首先预处理这些值

        int n,m;char ch;scanf("%d%d",&n,&m);
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++) {
			cin>>ch;	if(ch=='F')	a[i][j]=true;
			l[i][j]=j;r[i][j]=j;up[i][j]=1;}
	for (int i=1; i<=n; i++)
		for (int j=2; j<=m; j++)
			if (a[i][j]&&a[i][j-1])	l[i][j]=l[i][j-1];
	for (int i=1; i<=n; i++)
		for (int j=m-1; j>=1; j--)
			if (a[i][j]&&a[i][j+1])	r[i][j]=r[i][j+1];

• 如下图这是 \(up[i][j]\) 该有的亚子
  
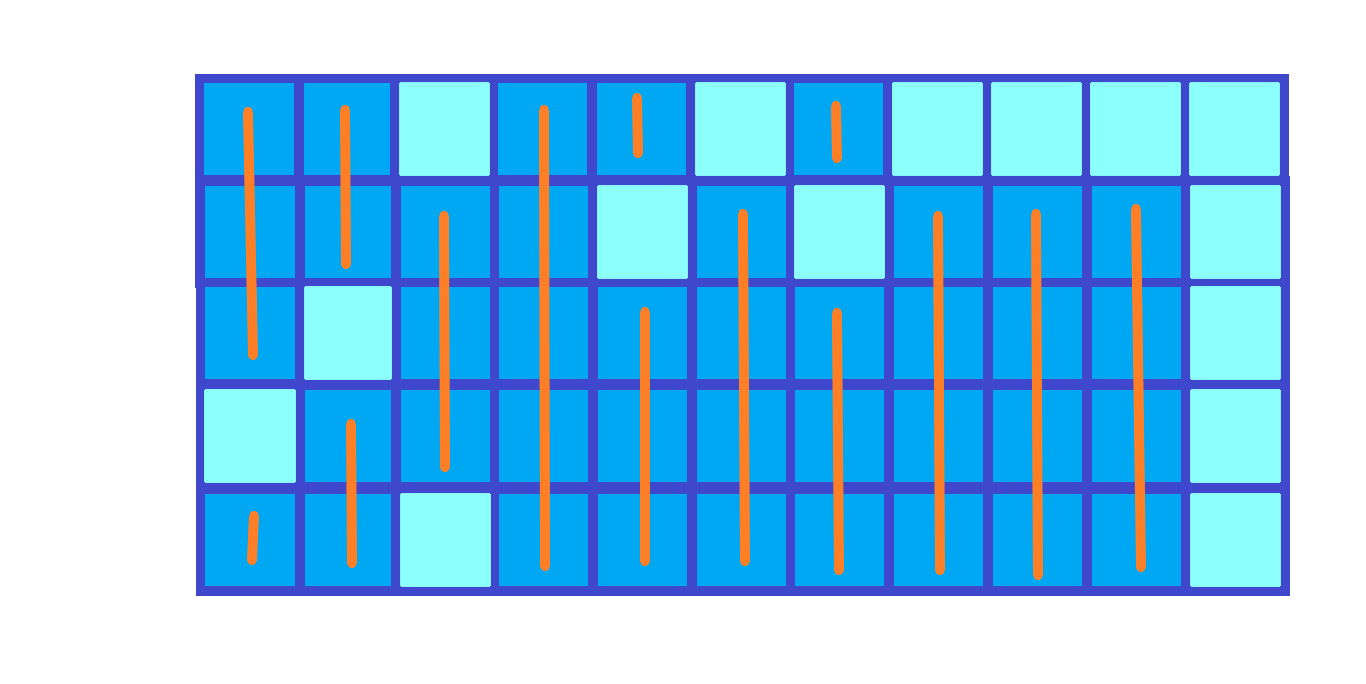
• 接下来对每个点求其能形成的矩阵 (以该点所在的水平为最低边)

        int ans=0;
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++) {
			if(a[i][j]&&a[i-1][j])
				r[i][j]=min(r[i-1][j],r[i][j]),
				l[i][j]=max(l[i-1][j],l[i][j]),//l[i][j]和r[i][j]都是坐标
				up[i][j]=up[i-1][j]+1;
			ans=max(ans,(r[i][j]-l[i][j]+1)*up[i][j]);
		}

• 下图为形成的矩阵
  
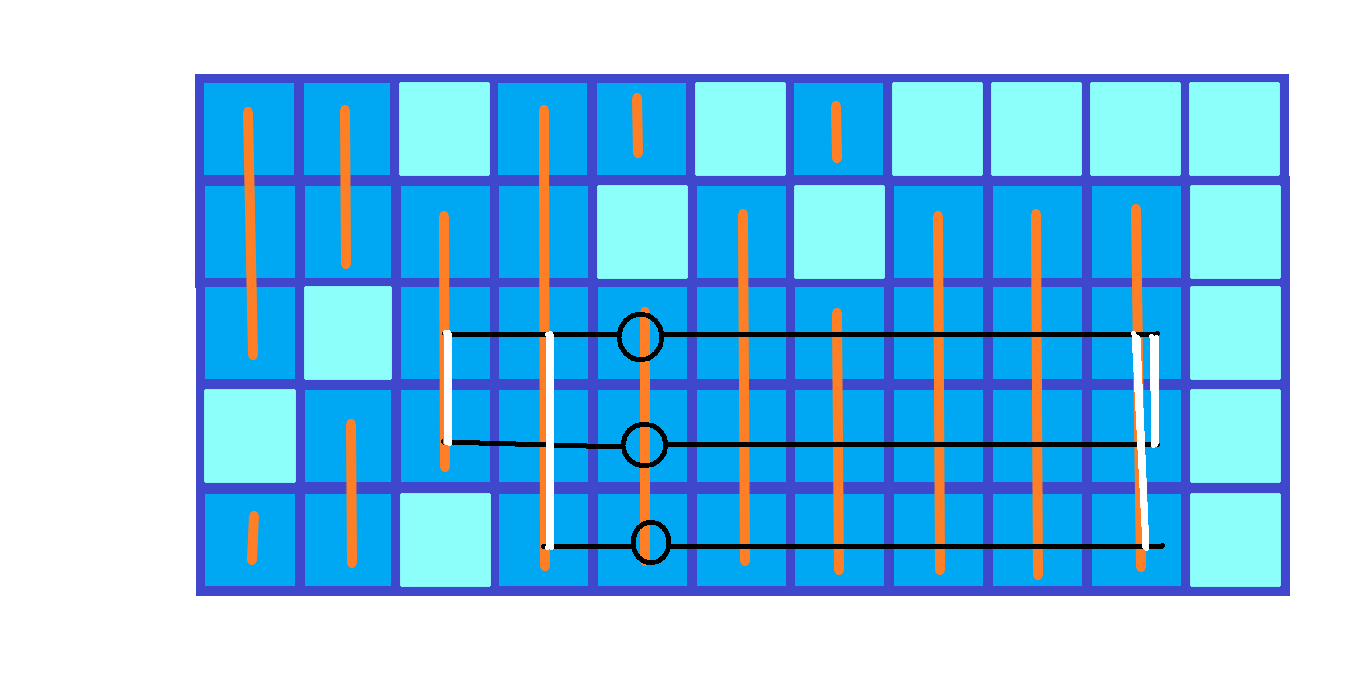
• 从上向下扫
  

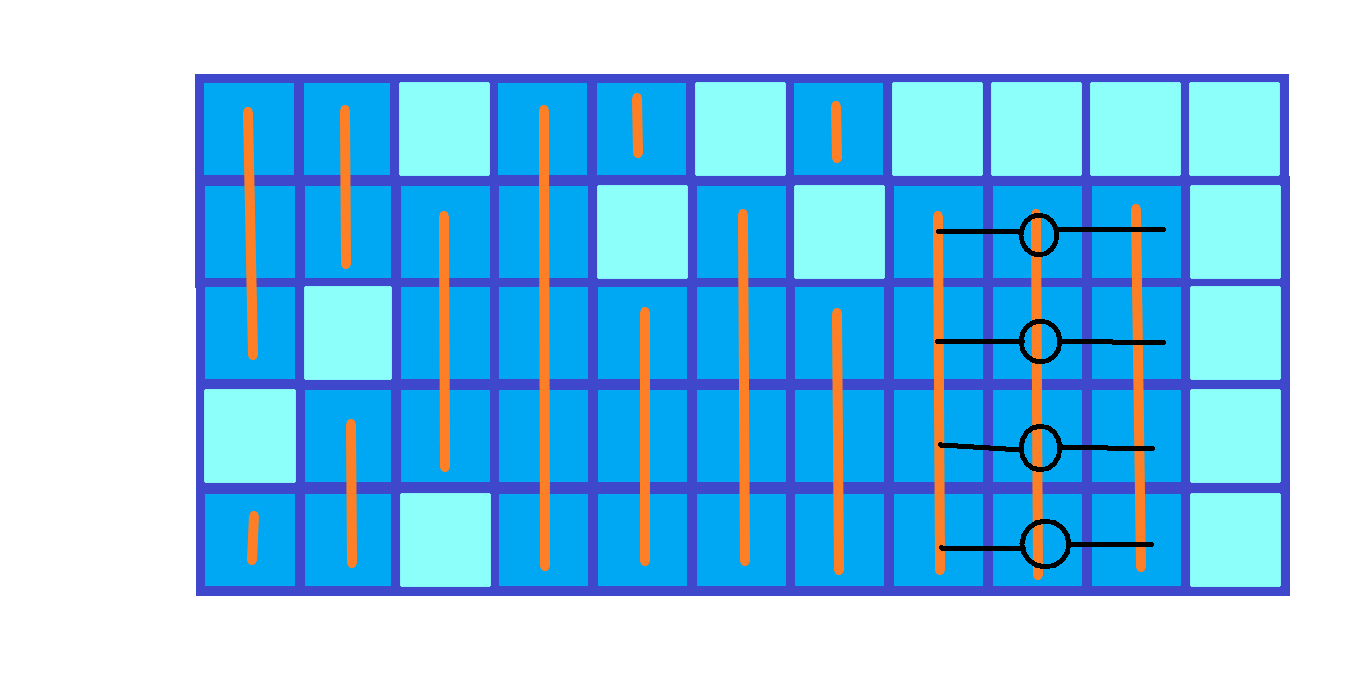
\(AC code\)

#include 
using namespace std;

const int M=2010;
int a[M][M],l[M][M],r[M][M],up[M][M],ans;

int main(){
	int n,m;char ch;scanf("%d%d",&n,&m);
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++) {
			cin>>ch;	if(ch=='F')	a[i][j]=true;
			l[i][j]=j;r[i][j]=j;up[i][j]=1;}
	for (int i=1; i<=n; i++)
		for (int j=2; j<=m; j++)
			if (a[i][j]&&a[i][j-1])	l[i][j]=l[i][j-1];
	for (int i=1; i<=n; i++)
		for (int j=m-1; j>=1; j--)
			if (a[i][j]&&a[i][j+1])	r[i][j]=r[i][j+1];
	int ans=0;
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++) {
			if(a[i][j]&&a[i-1][j])
				r[i][j]=min(r[i-1][j],r[i][j]),
				l[i][j]=max(l[i-1][j],l[i][j]),
				up[i][j]=up[i-1][j]+1;
			ans=max(ans,(r[i][j]-l[i][j]+1)*up[i][j]);
		}
	printf("%d\n",ans*3);
	return 0;
}