模式匹配——从BF算法到KMP算法

参考：https://blog.csdn.net/ns_code/article/details/19286279
https://blog.csdn.net/FightLei/article/details/52712461

一、模式匹配

子串的定位操作通常称为串的模式匹配。模式匹配的应用很常见，比如在文字处理软件中经常用到的查找功能。我们用如下函数来表示对字串位置的定位：

int index(const string &Tag,const string &Ptn,int pos)

其中，Tag为主串，Ptn为子串（模式串），如果在主串Tag的第pos个位置后存在与子串Ptn相同的子串，返回它在主串Tag中第pos个字符后第一次出现的位置，否则返回-1。

二、BF算法

我们先来看BF算法(Brute-Force，最基本的字符串匹配算法)，BF算法的实现思想很简单：我们可以定义两个索引值i和j，分别指示主串Tag和子串Ptn当前正待比较的字符位置，从主串Tag的第pos个字符起和子串Ptn的第一个字符比较，若相等，则继续逐个比较后续字符，否则从主串Tag的下一个字符起再重新和子串Ptn的字符进行比较，重复执行，直到子串Ptn中的每个字符依次和主串Tag中的一个连续字符串相等，则匹配成功，函数返回该连续字符串的第一个字符在主串Tag中的位置，否则匹配不成功，函数返回-1。

用C++代码实现如下：

/*
返回子串Ptn在主串Tag的第pos个字符后(含第pos个位置)第一次出现的位置，若不存在，则返回-1
采用BF算法，这里的位置全部以从0开始计算为准，其中T非空，0<=pos<=Tlen
*/
int index(const string &Tag,const string &Ptn,int pos)
{
	int i = pos;  //主串当前正待比较的位置，初始为pos
	int j = 0;   //子串当前正待比较的位置，初始为0
	int Tlen = Tag.size();  //主串长度
	int Plen = Ptn.size();  //子串长度
	
	while(i= Plen)
		return i - Plen;
	else
		return -1;
}

调用上面的函数，采用如下代码测试：

int main()
{
	char ch;
	do{
		string Tag,Ptn;  
		int pos;
		cout<<"输入主串：";
		cin>>Tag;
		cout<<"输入子串：";
		cin>>Ptn;
		cout<<"输入主串中开始进行匹配的位置（首字符位置为0）：";
		cin>>pos;
	
		int result = kmp_index(Tag,Ptn,pos);
		if(result != -1)
			cout<<"主串与子串在主串的第"<>ch;
	}while(ch == 'y' || ch == 'Y');
	return 0;
}

测试结果如下：

以上算法完全可以实现要求的功能 ，而且在字符重复概率不大的情况下，时间复杂度也不是很大，一般为O（Plen+Tlen）。但是一旦出现如下情况，时间复杂度便会很高，如：子串为“111111110”，而主串为 “111111111111111111111111110” ，由于子串的前8个字符全部为‘1’，而主串的的前面一大堆字符也都为1，这样每轮比较都在子串的最后一个字符处出现不等，因此每轮比较都是在子串的最后一个字符进行匹配前回溯，这种情况便是此算法比较时出现的最坏情况。
因此该算法在最坏情况下的时间复杂度为O（Plen*Tlen），另外该算法的空间复杂度为O（1）。

三、KMP算法

（1）主要思想

此算法是由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现的，因此该算法被称为克努斯-莫里斯-普拉特操作，简称为KMP算法。

KMP算法，是不需要对目标串S进行回溯的模式匹配算法。读者可以回顾上面的例子，整个过程中完全没有对目标串S进行回溯，而只是对模式串T进行了回溯。通过前面的分析，我们发现这种匹配算法的关键在于当出现失配情况时，应能够决定将模式串T中的哪一个字符与目标串S的失配字符进行比较。所以呢，那三位前辈就通过研究发现，使用模式串T中的哪一个字符进行比较，仅仅依赖于模式串T本身，与目标串S无关。

（2）求解next数组

根据next数组的特性，匹配过程中一旦出现S[i] != T[j]，则用T[next[j]]与S[i]继续进行比较，这就相当于将模式串T向右滑行j - next[j]个位置，示意图如下：

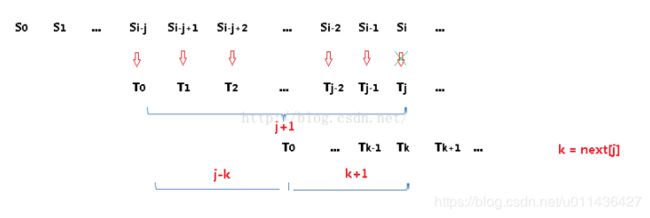
理解上面这幅图是理解next数组的关键，为了绘图简单，使用k 来表示next[j]。图中，j+1表示模式串T的字符个数，当出现失配情况时，使用T[next[j]]与S[i]进行比较，即图中T[k]与S[i]进行比较。因此右边括起来的是T[0]~T[k]共k+1个字符，因此左边括起来的是j + 1 - (k + 1) = j - k个字符，即向右滑行了j-next[j]个位置。

当上图中出现失配后可以得到如下信息：

S[i-j] = T[0]，S[i-j+1] = T[1]，…，S[i-k] = T[j-k]，S[i-k+1] = T[j-k+1]，…，S[i-2] = T[j-2]，S[i-1] = T[j-1]

模式串T进行右滑后，如图中所示必须保证：

S[i-k] = T[0]，S[i-k+1] = T[1]，S[i-k+2] = T[2]，…，S[i-2] = T[k-2]，S[i-1] = T[k-1]

通过上面两个式子可得：

T[0] = T[j-k]，T[1] = T[j-k+1]，T[2] = T[j-k+2]，…，T[k-2] = T[j-2]，T[k-1] = T[j-1]

它的含义表示对于模式串T中的一个子串T[0]_{T[j-1]，K的取值需要满足前K个字符构成的子序列（即T[0]}T[k-1]，称为前缀子序列）与后K个字符构成的子序列（即T[j-1]~T[j-k]，称为后缀子序列）相等。满足这个条件的K值有多个，取最大的那个值。

由此求解next数组问题，便被转化成了求解最大前缀后缀子序列问题。

再通过一个例子来说明最大前缀后缀子序列分别是什么？

对于子串“aaabcdbaaa”，满足条件的K值有1,2,3，取最大K值即3做为next[j]的函数值。此时的最大前缀子序列为“aaa”，最大后缀子序列为“aaa”。

再比如子串“abcabca”，其相等的最大前缀后缀子序列即为“abca”

	public static int[] getNext(String t) {
		int[] next = new int[t.length()];
		next[0] = -1;
		int suffix = 0;  // 后缀
		int prefix = -1;  // 前缀
		while (suffix < t.length() - 1) {
			//若前缀索引为-1或相等，则前缀后缀索引均+1
			if (prefix == -1 || t.charAt(prefix) == t.charAt(suffix)) {
				++prefix;
				++suffix;
				next[suffix] = prefix;  //1  
			} else {
				prefix = next[prefix];  //2
			}
		}
		return next;
	}

代码其实并不复杂，整体思路是分别以T[0]~T[suffix]为子串，依次求这些子串的相等的最大前缀后缀子序列，即next[suffix]的值。
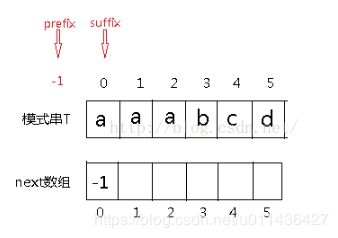
比较难理解的应该是有两处，我分别用1和2标示了出来。我们依次来看。初始化的过程如下图所示，prefix指向-1，suffix指向0，next[0] = -1。

if条件中prefix = -1成立，所以进入if语句，prefix = prefix+1，suffix = suffix+1，此时直接将next[suffix]赋值为prefix。即next[1] = 0。prefix+1到底代表的是什么？next[suffix]又代表的是什么？

next[suffix]表示的是不包括suffix即T[0]~T[suffix-1]这个子串的相等最长前缀后缀子序列的长度。意思是这个子串前面有next[suffix]个字符，与后面的next[suffix]个字符相等。

代码中suffix+1以后值为1，prefix+1以后值为0，next[1]表示的是对于子串“a”，它的相等最长前缀后缀子序列的长度，即为prefix，0。prefix一直表示的就是对于子串T[0]~T[suffix-1]前面有prefix个字符与后面prefix个字符相等，就是next[suffix]

继续往下走，满足if条件T[0] = T[1]，则suffix+1值为2，prefix+1以后值为1，next[2] = 1，表示子串“aa”，有长度为1的相等最长前缀后缀子序列“a”。

继续往下走，满足if条件T[1] = T[2]，则suffix+1值为3，prefix+1以后值为2，next[3] = 2，表示子串“aaa”，有长度为2的相等最长前缀后缀子序列“aa”。

至此，应该就可以明白next数组的所有设计了，下面的可以完全不用看

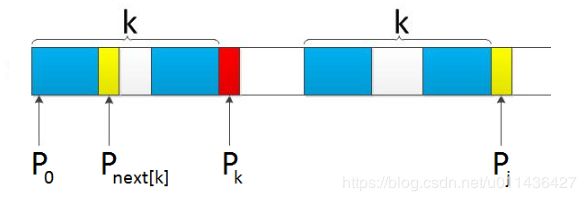
当再继续往下走时会发现T[2] != T[3]，不满足条件，则进入了else语句，prefix进行了回溯，prefix = next[prefix]，这就遇到了第二个难点，为什么要如此进行回溯呢？

借用网上的一张图来回答这个问题

这张图网上很多，但是详细描述这张图的具体含义的却很少。图中的j就对应代码中的suffix，k就对应代码中的prefix，模式串T图中用的P表示。

现在它们也遇到了这个问题，Pj] != P[k]，然后k进行了回溯，变为next[k]。既然prefix能走到k，suffix能走到j，则至少能保证对于子串P[0] ~ P[j-1]，前面有k个字符与后面k个字符相等。即图中前后方的蓝色区域。要是满足条件P[k] = P[j]则说明对于子串P[0] ~ P[j]，前面有k+1个字符与后面k+1个字符相等。但是现在不满足，则说明对于子串P[0] ~ P[j]不存在长度为k+1的相等最长前缀后缀子序列，可能存在比k+1小的最长前缀后缀子序列，可能是k，可能是k-1，k -2 , k -3 …或者根本就没有是0。那么我们的正常思路应该是回溯到k再进行判断，不存在k个则再回溯到k-1个，以此类推，那么算法中为什么是直接回溯到next[k]呢？

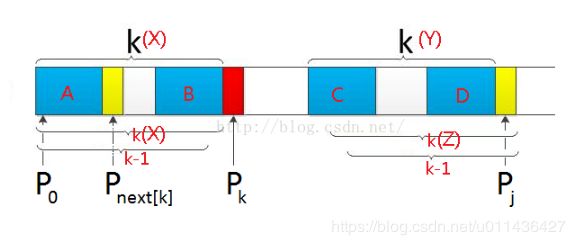
为了便于描述，我将图中的不同区域使用大写字母进行标注。前面说过正常思路是不存在k+1个，就回溯到k个进行判断，现在我们来看为什么不回溯到k？当回溯到k时，需要满足的条件是X区域的字符与Z区域的字符相等，而我们已知的是X区域的字符与Y区域的字符相等，若要满足条件，则需要Y区域字符与Z区域字符相等，从图中可以看到，Y区域与Z区域的字符仅相差一位，实际上比较的是Y区域的第一个字符与第二个字符，第二个字符与第三个字符等等，所以除非是Y区域的字符全部相等，是同一个字符，否则是不可能满足条件的。然而当Y区域的字符全部相等时，则X区域的字符也全部相等，那么next[k]就等于k，所以不如直接就回溯到next[k]。

那为什么直接回溯到next[k]就一定会满足条件呢？

已知的是X区域等于Y区域，所以B区域一定等于D区域，因为B区域表示X区域的后next[k]个字符，D区域表示Y区域的后next[k]个字符。

而next[k]的含义就是对于子串P[0] ~ P[k-1]，前面有next[k]个字符与后面next[k]个字符相等，即A区域等于B区域，所以可以得到A区域一定等于D区域，因此当下次比较满足条件P[next[k]] = P[j]时，就一定有长度为next[k] + 1的相等最长前缀后缀子序列。

next数组的求解搞清楚了，接下来我们就可以给出KMP算法的完整实现了

	public static int KMP(String s, String t) {
		int i = 0;
		int j = 0;
		//得到next数组
		int[] next = getNext(t);
		while (i < s.length() && j < t.length()) {
			if (j == -1 || s.charAt(i) == t.charAt(j)) {
				i++;
				j++;
			} else {
				//根据next数组的指示j进行回溯，而i永远不会回溯
				j = next[j];
			}
		}
		if (j == t.length()) {
			return i - j;
		} else {
			return -1;
		}
	}