D*(Dynamic A*) 算法详细解析
目录
- 记号
- 算法描述
- 参考
最初是Anthony Stentz发表在ICRA上,《Optimal and Efficient Path Planning for Partially-Known Environments》
记号
1) G G G:终点
2) X X X:表示当前节点,用 b ( X ) = Y b(X)=Y b(X)=Y表示 Y Y Y是 X X X的下一个节点,称为后向指针(backpointer),通过后向指针,很容易获得一条从起点到终点的路径。
3) c ( X , Y ) c(X,Y) c(X,Y):从 X X X到 Y Y Y的cost,对于不存在边的两个节点, c ( X , Y ) c(X,Y) c(X,Y)可定义为无穷大。
4)同 A ∗ A^* A∗ 一样, D ∗ D^* D∗ 也用 O P E N OPEN OPEN表和 C L O S E D CLOSED CLOSED表来保存待访问和已经访问的节点。对每个节点 X X X,用 t ( X ) t(X) t(X)来表示 X X X的状态, N E W NEW NEW表示未添加到 O P E N OPEN OPEN, O P E N OPEN OPEN表示当前处于 O P E N OPEN OPEN list, C L O S E D CLOSED CLOSED表示已从 O P E N OPEN OPEN list剔除。
5)同 A ∗ A^* A∗ 一样, D ∗ D^* D∗ 也有一个对目标的估计函数, h ( G , X ) h(G,X) h(G,X),不同的是, D ∗ D^* D∗ 还多了一个key函数,对于在 O P E N OPEN OPEN list中的每个节点, k ( G , X ) k(G,X) k(G,X)的定义原文中为“be equal to the minimum of h ( G , X ) h(G,X) h(G,X) before modification and all valuses assumed by h ( G , X ) h(G,X) h(G,X) since X X X was placed on the O P E N OPEN OPEN list”。也就是说,h函数会随着拓扑结构的变化而变化,key始终是h中最小的那一个。key函数将 O P E N OPEN OPEN中的节点 X X X分为两类,一类记为 R A I S E RAISE RAISE,如果 k ( G , X ) < h ( G , X ) k(G,X)<h(G,X) k(G,X)<h(G,X),另一类记为 L O W E R LOWER LOWER,如果 k ( G , X ) = h ( G , X ) k(G,X)=h(G,X) k(G,X)=h(G,X)。也就是说, k ( G , X ) ≤ h ( G , X ) k(G,X) \leq h(G,X) k(G,X)≤h(G,X),小于的情况如前方出现障碍物导致某些边的cost增加,等于的情况如前方cost不变或由于障碍物移动导致某些边cost减小。
6) k m i n k_{min} kmin和 k o l d k_{old} kold,前者表示当前 O P E N OPEN OPEN中key的最小值,后者表示上一次的最小值。
7)如果一系列节点 X 1 , X 2 , . . . , X N {X_1,X_2,...,X_N} X1,X2,...,XN满足 b ( X i + 1 ) = X i b(X_{i+1})=X_{i} b(Xi+1)=Xi,则称为一个序列(sequence)。一个序列表示了一条从 X N X_N XN到 X 1 X_1 X1的路径。在静态路径规划中,我们通常找的是一条从起点到终点的路径中,但是在动态路径规划中,起点是不断变化的,严格来讲应该是找寻一条从当前节点到终点的路径。显然这种情况下,考虑从终点到当前节点更为方便,故这里 X 1 X_1 X1反而是最靠近终点的节点。称一个序列为单调(monotonic)的如果满足 t ( X i ) = C L O S E D a n d h ( G , X i ) < h ( G , X i + 1 ) t(X_i)=CLOSED\ and\ h(G,X_i)<h(G,X_{i+1}) t(Xi)=CLOSED and h(G,Xi)<h(G,Xi+1)或者 t ( X i ) = O P E N a n d k ( G , X i ) < h ( G , X i + 1 ) t(X_i)=OPEN\ and\ k(G,X_i)<h(G,X_{i+1}) t(Xi)=OPEN and k(G,Xi)<h(G,Xi+1)。杂乱无序的序列是没有意义的,单调的序列其实就是我们要找的一条合理的路径。
8)对 X i , X j X_i,X_j Xi,Xj,如果 i < j i<j i<j则称 X i X_i Xi是 X j X_j Xj的祖先(ancestor),反之则称为后代(descendant)。
9)如果记号涉及两个节点且其中一个为终点,略去终点,如 f ( X ) = f ( G , X ) f(X)=f(G,X) f(X)=f(G,X)
算法描述
D ∗ D^* D∗主要包括两个部分, P R O C E S S − S T A T E PROCESS-STATE PROCESS−STATE和 M O D I F Y − C O S T MODIFY-COST MODIFY−COST,前者用来计算终点到当前节点的最优cost,后者用来修正cost。主要流程如下:
1)将所有节点的 t a g tag tag设置为 N E W NEW NEW, h ( G ) h(G) h(G)设为0,将G放置在 O P E N OPEN OPEN中。
2)重复调用 P R O C E S S − S T A T E PROCESS-STATE PROCESS−STATE直到当前节点 X X X从 O P E N OPEN OPEN中移除,即 t ( X ) = C L O S E D t(X)=CLOSED t(X)=CLOSED,说明此时已经找到一条从X出发到达终点的路径。
3)根据2)中获得的路径,从节点 X X X往后移动,直到达到终点或者检测到cost发送变化。
4)当cost发生变化时,调用第二个函数 M O D I F Y − C O S T MODIFY-COST MODIFY−COST,并将因为障碍物而cost受到影响的节点重新放入 O P E N OPEN OPEN中。假设 Y Y Y是发现状态时机器人所处的节点。通过调用 P R O C E S S − S T A T E PROCESS-STATE PROCESS−STATE直到 k m i n ≥ h ( Y ) k_{min} \geq h(Y) kmin≥h(Y),此时cost的变化已经传播到 Y Y Y,因此可以找到一条新的从 Y Y Y到终点的最优路径。
论文中的伪代码如下:
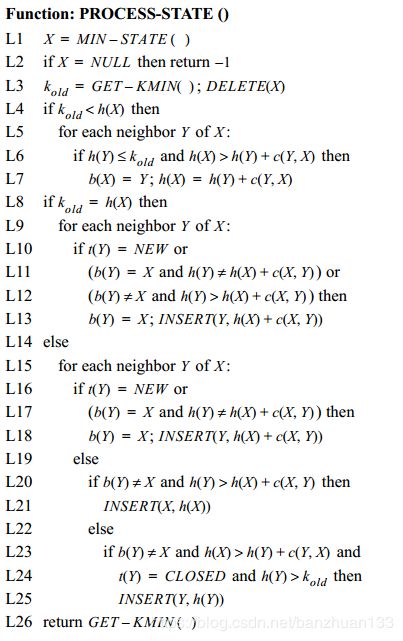
这里 M I N − S T A T E MIN-STATE MIN−STATE和 G E T − M I N GET-MIN GET−MIN的区别是前者返回的是具有最小 k k k值的节点,后者返回的是 k m i n k_{min} kmin。而 I N S E R T ( X , h n e w ) INSERT(X,h_{new}) INSERT(X,hnew)则是按照 t ( X ) t(X) t(X)的状态分为三种情况:
a) t ( X ) = N E W , k ( X ) = h n e w t(X)=NEW,k(X)=h_{new} t(X)=NEW,k(X)=hnew
b) t ( X ) = O P E N , k ( X ) = m i n ( k ( X ) , h n e w ) t(X)=OPEN,k(X)=min(k(X),h_{new}) t(X)=OPEN,k(X)=min(k(X),hnew)
c) t ( X ) = C L O S E D , k ( X ) = m i n ( h ( X ) , h n e w ) , h ( X ) = h n e w a n d t ( X ) = O P E N t(X)=CLOSED,k(X)=min(h(X),h_{new}),h(X)=h_{new} \ and\ t(X)=OPEN t(X)=CLOSED,k(X)=min(h(X),hnew),h(X)=hnew and t(X)=OPEN
最后一个条件就是针对已规划路径cost发生变化的状态。
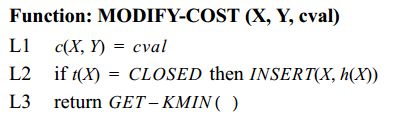
梳理一下上述流程
1)在静态条件下,利用Dijkstra或A*算法找到一条最优路径,同时利用后向指针确定每个节点的下一节点。
2)机器人从起点出发,沿路径移动,考虑最简单的情况,假设机器人的传感器范围为1,也就是说,只要下一个节点没有障碍物,就移动到下一个节点。
3)假设下一节点出现障碍物,怎么进行 M O D I F Y − C O S T MODIFY-COST MODIFY−COST呢?参考伪代码,当某个节点出现障碍物了,可以认为 h n e w = ∞ h_{new}=\infty hnew=∞,也就是说,这时 k k k仍是无障碍时的值,而 h h h已经变成无穷了,并且, X X X被重新放入 O P E N OPEN OPEN中。
4)放入 O P E N OPEN OPEN当然是要重新规划,这里就涉及到一个关键问题了
已经有 h h h函数了,为什么还要定义 k e y key key函数?
其实这里的 h h h函数应该和 A ∗ A^* A∗中的 f f f函数是等价的,虽然只有到终点的开销,但是因为 D ∗ D^* D∗是终点开始的,起点就是当前节点 X X X,所以可以认为 h ( X ) = 0 , f ( X ) = g ( X ) + h ( X ) = g ( X ) h(X)=0,f(X)=g(X)+h(X)=g(X) h(X)=0,f(X)=g(X)+h(X)=g(X)。在静态情况下,直接用 h ( X ) h(X) h(X)作为排序,是可以找到一条全局最优路径的(实际就是Dijkstra)。在动态情况下,假设现在下一节点 Y Y Y变成了不可达,那么相应的 h ( X ) = ∞ h(X)=\infty h(X)=∞,将 X X X状态添加进 O P E N OPEN OPEN list,那么 X X X节点就是排在 O P E N OPEN OPEN list的最后。也就是说,此时会从 O P E N OPEN OPEN list 剩余处于 O P E N OPEN OPEN状态的节点开始,一直到扩张全图都没有不可达节点之后,才会访问 X X X,这显然是不合理的。我们的目的就是要减少搜索空间,提高效率。用最小 h h h作为 k e y key key来排序,表示这里曾经有一条捷径,那么我优先在这附近搜索,进一步的,当障碍物消失,也能第一时间恢复到最短路径。
那么接下来就是最关键的步骤,怎么通过局部调整避开障碍物找到一条合理的路径(实际是贪心的最优)。
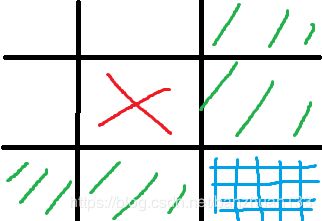
5)此时 P R O C E S S − S T A T E PROCESS-STATE PROCESS−STATE进入的是 L 4 − L 7 L4-L7 L4−L7,注意,这里我们最简单的想法应该是找到除了Y之外最短的路径,也就是循环迭代 H ( X ) > H ( Y ) + C ( Y , X ) H(X)>H(Y)+C(Y,X) H(X)>H(Y)+C(Y,X),但是作者这里加了一个条件, h ( Y ) ≤ k o l d h(Y)\leq k_{old} h(Y)≤kold,初衷很好理解,我可以绕障碍物,但是不能绕太远,还是要往终点的方向靠。但也有一个新的问题,假设估计采用的是曼哈顿距离,邻域考虑最简单的八邻域,那么如下图所示,红色是当前节点,蓝色是初始规划的下一节点,此时被障碍物占据,满足 h ( Y ) ≤ k o l d h(Y)\leq k_{old} h(Y)≤kold的节点用绿色表示,考虑极端情况,所有绿色格子也被障碍物占据,此时算法会陷入死循环(去掉该条件则不会)。这里暂时不考虑极端情况,沿着作者的思路走(我们可以默认在已知环境中突然出现大量的障碍物概率很小)。
6)在5)中我们找到一个当前最优的下一节点,注意,因为这里是贪心策略,所以并没有考虑到下一节点是否是可行的(可能下一节点的下一节点仍然是被阻塞的)。这样做的好处是尽可能地利用了之前已经探索的区域,减少了搜索空间,坏处就是可能会绕远路。
7)上述过程的终止条件, k m i n ≥ h ( Y ) k_{min}\geq h(Y) kmin≥h(Y),也就是说,当前所有处于 O P E N OPEN OPEN状态的节点,都不可能再降低cost了,那么自然也就没有继续搜索的必要了。从而就完成了一次路径的修正。
8)这里考虑的是cost增加的情况,实际cost减少的情况也是类似的。
参考
Optimal and Efficient Path Planning for Partially-Known Environments
https://blog.csdn.net/lqzdreamer/article/details/85055569#_437