数据结构：BF算法，KMP算法之C、C++的实现

数据结构中BF算法，KMP算法的实现

 这是我上《数据结构》实验课的作业，我会基于严蔚敏老师的《数据结构（c语言）》版本，注解原代码，给出基于我自身理解的解释，严老师的解释很清晰，大家可以把我的当做一种补充，之后会根据自己理解编写面向对象C++的代码。

1. BF算法

原代码的注释：

int Strlength(SString S){}//返回串的长度
//返回子串T在主串S中第pos个字符之后的位置，不存在值为0
//T非空，1<=pos<=strlength(S)
int Index(SString S, SString T, int pos){//1
    if (pos<1 || pos > Strlength(S))return -1;//2
    int i = pos, j = 1;
    while (i <= S[0] && j <= T[0]){//3
        if (S[i] == T[j]){ ++i; ++j; }//4
        else { i = i - j + 2; j = 1; }//5
    }
    if (j > T[0])return i - T[0];//6
    else return 0;//7
}
//1这玩意就是个暴力算法
//2如果pos超出主串的长度，那么就无法给出值，返回错误
//3串的首位存储串的长度，所以如果pos的位置在主串长度之内，j是指向模式串的指针，所以j也要在模式串的长度之内移动
//4如果从pos开始的第一个字符和子串的第一个字符相等，那么主串和子串都向后移动1位
//5如果移动了j次以后，主串和子串不相等，那么模式串的指针归1，主串定位在开始比较的主串的后一位,i=i-j+2解释在下面
//6如果j大于子串的长度，那么就是子串完全遍历，就是匹配了，那么初始位置就是 i - T[0]
//7如果j<=T[0]，那么便是没有没有匹配成功，不存在，就输出0

对注释5的补充：

 首先，我们看这张图，S行是主串，T行是模式串，假设我们S行的第三个元素值是a，当模式串和主串相比较，i是指向主串的指针，j是指向模式串的指针，假设本次匹配：
* i从3开始，j从1开始，如果相匹配，那么i和j都后移一位，那么直到i=11,j=9会发生不匹配
* 那么在BF算法中，i左移至4，j左移至1开始重新匹配
* i要移动的范围是4~11，相当于j移动的长度减去1，所以i=i-(j-1)+1=i-j+2;

C++的调试成功的代码：

//入口
#include "stdafx.h"
#include 
#include
#include
using namespace std;
const int MAXSTRLEN = 255;
//S用来存储主串，T用来存储模式串
class SString{
public:
    SString(char *b){ ch = b; };//重载构造函数,这是用来记录主串的
    ~SString(){};//析构函数
    int get_length(){
        length = strlen(ch);
        return length;
    };
public:
    int length;//用来记录串的长度
    char *ch;//顺序串动态存储空间首地址，按串的实际长度分配空间
};
//BF算法
int Index(SString S, SString T, int pos){//1
    int i = pos - 1;//因为数组是从0开始的，所以i就代表了第pos个字符的位置
    if (i<0 || i> S.get_length())return -1;//2
    int  j = 0;
    while (i < S.get_length() && j < T.get_length()){//3
        if (S.ch[i] == T.ch[j]){ ++i; ++j; }//4
        else { i = i - j + 1; j = 0; }//5
    }
    if (j >= T.get_length())return i - T.get_length()+1;//6
    else return 0;//7
}
int main(){
    char b[] = "adhgjfekdi";
    SString myString2(b);//用于存储主串的对象
    cout << "主串的内容为：";
    for (int i = 0; i < myString2.get_length(); i++)cout << myString2.ch[i];
    cout<char *c;
    c = "hgj";
    SString myString(c);//用于存储模式串的对象
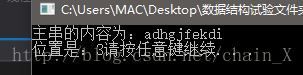
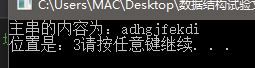
    cout << "位置是：" << Index(myString2, myString, 1);
    system("pause");
}

效果图（忽视水印）：

2. KMP 算法

 因为KMP算法是暴力算法的改进，所以不一样的地方也就以下三点，注释写在代码下面：

int Index_KMP(SString S, SString T, int pos){
    int i = pos; int j = 1;//同BF算法
    while (i <= S[0] && j <= T[0]){//同BF算法
        if (j == 0 || S[i] == T[j]){ ++i, ++j; }//1
        else j = next[j];//2
    }
    if (j > T[0])return i - T[0];//同BF算法
    else return 0;//同BF算法
}
//其中next的获取如下：
void get_next(SString T, int next[]){//3
    int j = 1; next[1] = 0; k = 0;//4
    while (j < T[0]){//5
        if (k == 0 || T[j] == T[k]){ ++j, ++k; next[j] = k; }//6
        else k = next[k];//7
    }
}
//1同6
//2同7
//3 这个函数是为了获得当模式串匹配到第j位时，主串中i可以最大右移的距离K,next[j]=k的k值
//4 j表示模式串中字符的位序，next[1]=0,表示当模式串中第一个位置就显示不匹配，那么主串右移一个位置，重新开始匹配；k初始化为0
//5指针移动要在模式串的长度内
//6解释见下文
//7解释见下文

首先，先解释一下原理：
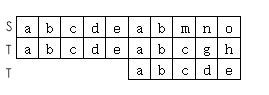
BF算法存在的浪费

 再来看这张图，在BF算法中，i=11,j=9的时候，遇到不匹配，就要左移至i=4，j=1的位置。
 观察此图，9，10位置和j的1，2位置是相同的，所以最经济的做法是从i=11，j=3开始进行重新匹配。

如何尽可能多移动，next的原理

原理：假设以指针i和j分别指示主串和模式串中正等待比较的字符，令i的初始值为pos，j的初始值为1。若在匹配过程中Si=Ti，那么i和j分别增加1，否则，i不变，令j退到next[j]的位置再比较，若相等，则指针各增加1，否则j再退到next[j]的位置。

---

在这边，提出一个前缀包含概念，这不是我的概念，详见：KMP算法详解,还有部分匹配【经典算法】——KMP，深入讲解next数组的求解

 重新画了一张图，观察这张图可知: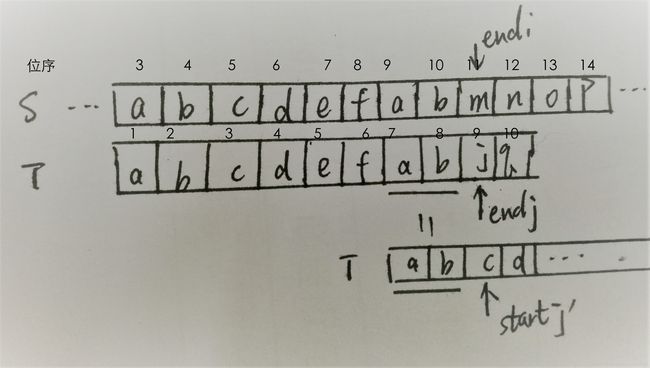

 因为在j=9之前有7，8两位和模式串的前两位是相等的，所以模式串可以直接从j=3开始和主串的i=11那一位相匹配。相当于模式串直接右移了8-2=6位，而主串就不用回溯了，那么模式串相当于移动j-k位（k=2为最大位移长度）。
前缀包含：ab就是模式串的一个前缀，而模式串中在7，8位又包含了该前缀。
 next数组的作用就是记录当匹配到模式串的第j位（1<=j<=T[0]）时，模式串能移动的最大位移长度。
 也可以理解为：当模式串中的第j个字符与主串比较不想等时，模式串应该从前面的第几个字符开始重新与主串比较。
 那就具有以下三种情况：
* 1：j=1，第一个字符就不相等：主串i=i+1，主串后移一位；模式串j=1；next[1]=0;模式串指针不后移。
* 2：next[j]=MAX{k|0 < k > j,T₁T₂ ……T_k-1=T_j-(k-1)T_j-(k-2)……T_j-1};能使得等式成立的最大k值。
* 3:0,other;

k的求取，我认为最好理解的时部分匹配概念：
“前缀”和”后缀”。 “前缀”指除了最后一个字符以外，一个字符串的全部头部组合；”后缀”指除了第一个字符以外，一个字符串的全部尾部组合。长度就是前后缀中相等的最大字符长度。
以“abcabe”为例。

字符段	前缀	后缀	长度
a	无	无	0
ab	a	b	0
abc	a,ab	c,bc	0
abca	a,ab,abc	bca,ca,a	1
abcab	a,ab,abc,abca	bcab,cab,ab,b	2
abcabe	a,ab,abc,abca,abcab	bcabe,cabe,abe,be,e	0

长度就是最大移动距离K；

代码注释

if (k == 0 || T[j] == T[k]){ ++j, ++k; next[j] = k; }//6
        else k = next[k];//7

//6：就是这种情况：

T ₁T ₂ ……T _k-1=T _j-(k-1)T _j-(k-2)……T _j-1
 1.如果存在T _k=T _j,那么，next[j+1]=next[j]+1;



//7：就是不等，那么模式串的指针就移动其能够移动的最大距离，从模式串的开头数的next[j]的长度。

C++的调试成功的代码：

#include "stdafx.h"
#include 
#include
#include
using namespace std;
const int MAXSTRLEN = 255;
//S用来存储主串，T用来存储模式串
class SString{
public:
    SString(char *b){ ch = b; };//重载构造函数,这是用来记录主串的
    ~SString(){};//析构函数
    int get_length(){
        length = strlen(ch);
        return length;
    };
public:
    int length;//用来记录串的长度
    char *ch;//顺序串动态存储空间首地址，按串的实际长度分配空间
};

int Index_KMP(SString S, SString T, int pos){
    //get_next
    int *next = new int[T.get_length()];
    next[0] = -1;
    int i1 = 0,j1 = -1;
    while (i1 < T.get_length()-1){
        if (j1 == -1 || T.ch[i1] == T.ch[j1])
        { ++i1, ++j1; next[i1] = j1; }
        else j1 = next[j1];
    }
    //KMP
    int i = pos-1; int j = 0;//同暴力算法
    while (i <= S.get_length()-1 && j <= T.get_length()-1){//1
        if (j == 0|| S.ch[i] == T.ch[j]){ ++i, ++j; }//2
        else j = next[j];//3
    }
    if (j >=T.get_length())return i - T.get_length()+1;//同暴力算法
    else return 0;//同暴力算法
}


int main(){
    char b[] = "adhgjfekdi";
    SString myString2(b);//用于存储主串的对象
    cout << "主串的内容为：";
    for (int i = 0; i < myString2.get_length(); i++)cout << myString2.ch[i];
    cout << endl;
    char *c;
    c = "hgj";
    SString myString(c);//用于存储模式串的对象
    cout << "位置是：" << Index_KMP(myString2, myString, 1);
    system("pause");
}

结果如图：