二分查找详细总结
二分查找总结
最近在做leetcode上二分查找的题目,看到了一篇文章,讲的很好,现在做个记录。
思路 我相信对很多读者朋友来说,编写二分查找的算法代码属于玄学编程,虽然看起来很简单,就是会出错,要么会漏个等号,要么少加个 1。
不要气馁,因为二分查找其实并不简单。看看 Knuth 大佬(发明 KMP 算法的那位)怎么说的:
Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky…
这句话可以这样理解:思路很简单,细节是魔鬼。
本文以问答的形式,探究几个最常用的二分查找场景:寻找一个数、寻找左侧边界、寻找右侧边界。第一个场景是最简单的算法形式,解决这道题,后两个场景就是本题。 而且,我们就是要深入细节,比如不等号是否应该带等号,mid是否应该加一等等。分析这些细节的差异以及出现这些差异的原因,保证你能灵活准确地写出正确的二分查找算法。
- 二分查找框架
Java版本
分析二分查找的一个技巧是:不要出现int binarySearch(int[] nums, int target) { int left = 0, right = ...; while(...) { int mid = (right + left) / 2; if (nums[mid] == target) { ... } else if (nums[mid] < target) { left = ... } else if (nums[mid] > target) { right = ... } } return ...; }else,而是把所有情况用else if写清楚,这样可以清楚地展现所有细节。本文都会使用else if,旨在讲清楚,读者理解后可自行简化。
其中 … 标记的部分,就是可能出现细节问题的地方,当你见到一个二分查找的代码时,首先注意这几个地方。后文用实例分析这些地方能有什么样的变化。
另外声明一下,计算 mid 时需要技巧防止溢出,即mid=left+(right-left)/2。因为当left和right都很大的时候,他们相加就会溢出,而这种方法不会溢出。以后最好使用这个来求mid。 - 寻找一个数(基本的二分搜索)
这个场景是最简单的,肯能也是大家最熟悉的,即搜索一个数,如果存在,返回其索引,否则返回 -1。
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) {
int mid = (right + left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}
- 为什么 while 循环的条件中是 <=,而不是 < ?
答:因为初始化 right 的赋值是nums.length-1,即最后一个元素的索引,而不是nums.length。
这二者可能出现在不同功能的二分查找中,区别是:前者相当于两端都闭区间 [left, right],后者相当于左闭右开区间 [left, right),因为索引大小为nums.length是越界的。
我们这个算法中使用的是前者 [left, right] 两端都闭的区间。这个区间其实就是每次进行搜索的区间,我们不妨称为「搜索区间」。
什么时候应该停止搜索呢?当然,找到了目标值的时候可以终止:
if(nums[mid] == target)
return mid;
但如果没找到,就需要 while 循环终止,然后返回 -1。那 while 循环什么时候应该终止?搜索区间为空的时候应该终 止,意味着你没得找了,就等于没找到嘛。
while(left <= right) 的终止条件是 left == right + 1,写成区间的形式就是 [right + 1, right],或者带个具体的数字进去 [3, 2],可见这时候搜索区间为空,因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的,直接返回 -1 即可。
while(left < right) 的终止条件是 left == right,写成区间的形式就是 [left, right],或者带个具体的数字进去 [2, 2],这时候搜索区间非空,还有一个数 22,但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了,索引 2 没有被搜索,如果这时候直接返回 -1 就是错误的。
当然,如果你非要用 while(left < right) 也可以,我们已经知道了出错的原因,就打个补丁好了
//...
while(left < right) {
// ...
}
return nums[left] == target ? left : -1;
- 为什么
left = mid + 1,right = mid - 1?我看有的代码是right = mid或者left = mid,没有这些加加减减,到底怎么回事,怎么判断?
答:这也是二分查找的一个难点,不过只要你能理解前面的内容,就能够很容易判断。
刚才明确了「搜索区间」这个概念,而且本算法的搜索区间是两端都闭的,即 [left, right]。那么当我们发现索引 mid 不是要找的 target 时,如何确定下一步的搜索区间呢?
当然是 [left, mid - 1] 或者 [mid + 1, right] 对不对?因为 mid 已经搜索过,应该从搜索区间中去除。 - 此算法有什么缺陷?
答:至此,你应该已经掌握了该算法的所有细节,以及这样处理的原因。但是,这个算法存在局限性。
比如说给你有序数组 nums = [1,2,2,2,3],target = 2,此算法返回的索引是 2,没错。但是如果我想得到 target 的左侧边界,即索引 1,或者我想得到 target 的右侧边界,即索引 3,这样的话此算法是无法处理的。
这样的需求很常见。你也许会说,找到一个 target,然后向左或向右线性搜索不行吗?可以,但是不好,因为这样难以保证二分查找对数级的复杂度了。
我们后续的算法就来讨论这两种二分查找的算法。
-
寻找左侧边界的二分搜索
直接看代码,其中的标记是需要注意的细节:int left_bound(int[] nums, int target) { if (nums.length == 0) return -1; int left = 0; int right = nums.length; // 注意 while (left < right) { // 注意 int mid = (left + right) / 2; if (nums[mid] == target) { right = mid; } else if (nums[mid] < target) { left = mid + 1; } else if (nums[mid] > target) { right = mid; // 注意 } } return left; }
- 为什么
while(left < right)而不是 <= ?
答:用相同的方法分析,因为right = nums.length而不是nums.length - 1。因此每次循环的「搜索区间」是 [left, right) 左闭右开。
while(left < right)终止的条件是left == right,此时搜索区间 [left, left) 为空,所以可以正确终止。 - 为什么没有返回 -1 的操作?如果 nums 中不存在 target 这个值,怎么办?
答:因为要一步一步来,先理解一下这个「左侧边界」有什么特殊含义:
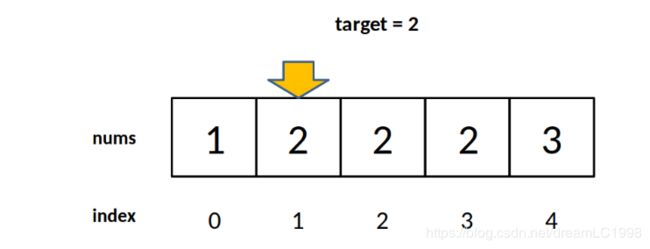
对于这个数组,算法会返回 1。这个 1 的含义可以这样解读:nums 中小于 2 的元素有 1 个。
比如对于有序数组 nums = [2,3,5,7], target = 1,算法会返回 0,含义是:nums 中小于 1 的元素有 0 个。
再比如说 nums 不变,target = 8,算法会返回 4,含义是:nums 中小于 8 的元素有 4 个。
综上可以看出,函数的返回值(即 left 变量的值)取值区间是闭区间 [0, nums.length],所以我们简单添加两行代码就 能在正确的时候 return -1:
while (left < right) {
//...
}
// target 比所有数都大
if (left == nums.length) return -1;
// 类似之前算法的处理方式
return nums[left] == target ? left : -1;
-
为什么 left = mid + 1,right = mid ?和之前的算法不一样?
答:这个很好解释,因为我们的「搜索区间」是 [left, right) 左闭右开,所以当 nums[mid] 被检测之后,下一步的搜索区间应该去掉 mid 分割成两个区间,即 [left, mid) 或 [mid + 1, right)。 -
为什么该算法能够搜索左侧边界?
答:关键在于对于 nums[mid] == target 这种情况的处理:if (nums[mid] == target) right = mid;
可见,找到 target 时不要立即返回,而是缩小「搜索区间」的上界 right,在区间 [left, mid) 中继续搜索,即不断向左收缩,达到锁定左侧边界的目的。
3. 为什么返回 left 而不是 right?
答:都是一样的,因为 while 终止的条件是 left == right。
4. 寻找右侧边界的二分查找
寻找右侧边界和寻找左侧边界的代码差不多,只有两处不同,已标注:
int right_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = (left + right) / 2;
if (nums[mid] == target) {
left = mid + 1; // 注意
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1; // 注意
}
-
为什么这个算法能够找到右侧边界?
答:类似地,关键点还是这里:if (nums[mid] == target) { left = mid + 1;当
nums[mid] == target时,不要立即返回,而是增大「搜索区间」的下界 left,使得区间不断向右收缩,达到锁定右侧边界的目的。 -
为什么最后返回
left - 1而不像左侧边界的函数,返回left?而且我觉得这里既然是搜索右侧边界,应该返回 right 才对。
答:首先,while 循环的终止条件是left == right,所以 left 和 right 是一样的,你非要体现右侧的特点,返回right - 1好了。
至于为什么要减一,这是搜索右侧边界的一个特殊点,关键在这个条件判断:if (nums[mid] == target) { left = mid + 1;
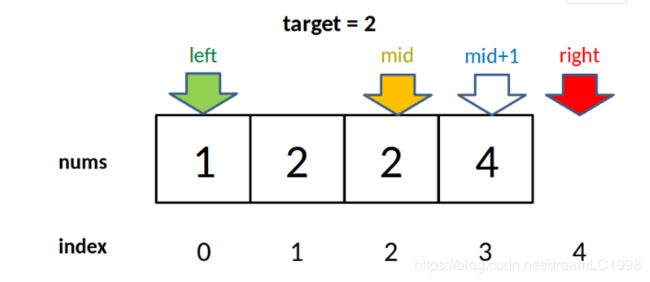
因为我们对 left 的更新必须是 left = mid + 1,就是说 while 循环结束时,nums[left] 一定不等于 target 了,而 nums[left-1] 可能是 target。
至于为什么 left 的更新必须是 left = mid + 1,同左侧边界搜索,就不再赘述。
-
为什么没有返回 -1的操作?如果 nums 中不存在 target 这个值,怎么办?
答:类似之前的左侧边界搜索,因为 while 的终止条件是left == right,就是说 left 的取值范围是[0, nums.length],所以可以添加两行代码,正确地返回 −1:while (left < right) { // ... } if (left == 0) return -1; return nums[left-1] == target ? (left-1) : -1;
- 最后总结
来梳理一下这些细节差异的因果逻辑:-
第一个,最基本的二分查找算法:
第一个,最基本的二分查找算法: 因为我们初始化 right = nums.length - 1 所以决定了我们的「搜索区间」是 [left, right] 所以决定了 while (left <= right) 同时也决定了 left = mid+1 和 right = mid-1 因为我们只需找到一个 target 的索引即可 所以当 nums[mid] == target 时可以立即返回 -
第二个,寻找左侧边界的二分查找:
因为我们初始化 right = nums.length 所以决定了我们的「搜索区间」是 [left, right) 所以决定了 while (left < right) 同时也决定了 left = mid + 1 和 right = mid 因为我们需找到 target 的最左侧索引 所以当 nums[mid] == target 时不要立即返回 而要收紧右侧边界以锁定左侧边界 -
第三个,寻找右侧边界的二分查找:
因为我们初始化 right = nums.length 所以决定了我们的「搜索区间」是 [left, right) 所以决定了 while (left < right) 同时也决定了 left = mid + 1 和 right = mid 因为我们需找到 target 的最右侧索引 所以当 nums[mid] == target 时不要立即返回 而要收紧左侧边界以锁定右侧边界 又因为收紧左侧边界时必须 left = mid + 1 所以最后无论返回 left 还是 right,必须减一
-
如果以上内容你都能理解,那么恭喜你,二分查找算法的细节不过如此。
通过本文,你学会了:
分析二分查找代码时,不要出现 else,全部展开成 else if 方便理解。
注意「搜索区间」和 while 的终止条件,如果存在漏掉的元素,记得在最后检查。
如需要搜索左右边界,只要在 nums[mid] == target 时做修改即可。搜索右侧时需要减一。
以后就算遇到其他的二分查找变形,运用这几点技巧,也能保证你写出正确的代码。