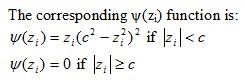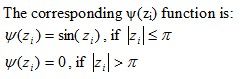M-estimator
在“Foreground Estimation Based on Linear Regression Model with Fused Sparsity on Outliers”这篇文献里,在介绍最小二乘对噪声不鲁棒的时候提到了一个新的东西叫做M-estimators,好像就是之前所说的M估计,在大学里老师好像提过这个东西,但如今我却不知道这究竟是个什么东东了!经网上查阅,把相关东西记录在此,“以儆效尤”。
转载自:http://www.statisticalconsultants.co.nz/blog/m-estimators.html
M-estimators
Statistical Analysis Techniques, Robust Estimators, Alternatives to OLS
The three main classes of robust estimators are M, L and R. Robust estimators are resistant to outliers and when used in regression modelling, are robust to departures from the normality assumption.
M-estimators are a maximum likelihood type estimator. M estimation involves minimizing the following:
Where ρ is some function with the following properties:
- ρ(r) ≥ 0 for all r and has a minimum at 0
- ρ(r) = ρ(-r) for all r
- ρ(r) increases as r increases from 0, but doesn’t get too large as r increases
For LAD:
ρ(r) = |r|
For OLS:
ρ(r) = r
2
Note that OLS doesn’t satisfy the third property, therefore it doesn’t count as a robust M-estimator.
In the case of a linear model, the function to minimise will be:
Instead of minimising the function directly, it may be simpler to use the function’s first order conditions set to zero:
where:
If the ρ function can be differentiated, the M-estimator is said
to be a ψ-type. Otherwise, the M-estimator is said to be a ρ-type.
Lp subclass
L
p is a subclass of M estimators. An L
p beta coefficient would be one that minimises the following:
Where 1≤ p ≤2.
If p=1, it is the equivalent of LAD and if p=2, it is the equivalent of OLS.
The lower p is, the more robust the L
p will be to outliers. The lower p is, the greater the number of iterations would be needed for the sum of |r|
p to converge at the minimum.
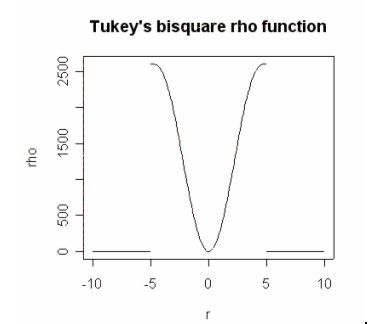
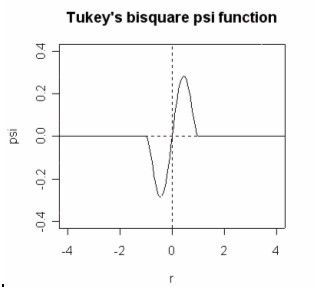
Tukey’s bisquare M-estimator
Tukey proposed an M-estimator that has the following ρ(z
i) function:
Where c is a constant and
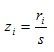 , where s is the estimated scale parameter.
, where s is the estimated scale parameter.
Tukey’s bisquare psi function leaves out any extreme outliers by giving them a zero weighting.
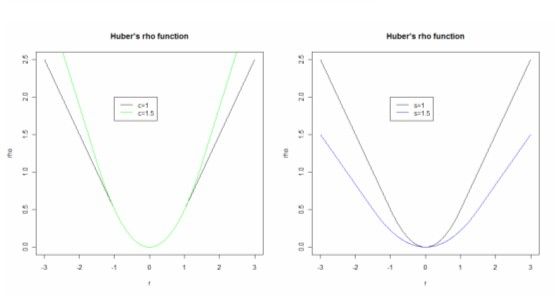
Huber's M-estimator
Huber proposed an M-estimator that has the following ρ(z
i) function:
Where c is a constant and
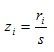 , where s is the estimated scale parameter.
, where s is the estimated scale parameter.
It essentially applies an LAD function to outliers and an OLS function to the other observations.
Andrews's M-estimator
Andrews (1974) proposed the following ρ(z
i) function:
Where
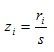 , where s is the estimated scale parameter.
, where s is the estimated scale parameter.
See also:
Regression
LAD
L-estimators
R-estimators