C/C++/Java代码 模式匹配、朴素的模式匹配算法、KMP算法模式匹配 数据结构【经典算法】详解
一、什么是模式匹配?
先看看某度的解释。。
模式匹配是数据结构中字符串的一种基本运算,给定一个子串,要求在某个字符串中找出与该子串相同的所有子串,这就是模式匹配。
二、常见模式匹配算法
-
朴素的模式匹配算法
-
KMP匹配算法
-
BM匹配算法
A.朴素的模式匹配算法
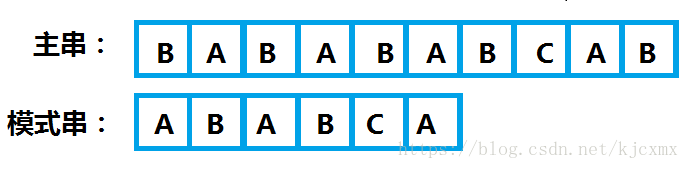
算法思想:从目标串的的第一个字符起与模式串的第一个字符比较,若相等,则继续对字符进行后续的比较,否则目标串从第二个字符起与模式串的第一个字符重新比较,直至模式串中的每个字符依次和目标串中的一个连续的字符序列相等为止,此时称为匹配成功,否则匹配失败。 如下例子:主串T为“BABABCAB”,模式串S为“ABCA”。
![]()
A、见下图BF.1开始第一步的匹配,i = 0,j = 0时,主串的值不等于模式串的值,则进行下一步,也就是 j++而也相应i++。
![]()
B、见下图BF.2开始第二步的匹配,T[1] = S[0],所以第一个字符是匹配的,那么将进行第二个字符的验证,也就是 j++而也相应i++。
![]()
C、见下图BF.3开始第二步的匹配,T[2] = S[1],所以S中第二个字符也是匹配的,那么将进行S中第三个字符的验证,也就是 j++而也相应i++。
![]()
D、见下图BF.4开始第三步的匹配,T[3] != S[3],所以S中第三个字符是不匹配的,那么将进行回溯,就是一下回到开始的位置,之前匹配的S[0]和S[1]的结果无效了。所以对于i来说赋值为i = 2,对应的j 将返回为j = 0,重复第A、B、C、以上步骤,这里省略。
![]()
E、见下图BF.5开始匹配,T[6] = S[3],所以S中第四个字符也是匹配的,因为模式串S结束,所以将匹配成功。
![]()
E、如果模式串为S="AAAA",则不会匹配成功,那么将会返回-1,匹配失败,对于时间复杂度来讲就是最坏情况。
代码详细的解释参见上篇的解读 三种语言(C/C++/Java)代码 链接:https://blog.csdn.net/kjcxmx/article/details/82350527
int BruteForce(string Text, string Pattern){
int lenT = Text.length();
int lenP = Pattern.length();
int s,i;
for (s = 0; s <= lenT-lenP; s++){
i = 0;
bool bEqual = true;
while (bEqual && (i < lenP)){
if (Text[s+i] == Pattern[i]){
i++;
}else{
bEqual = false;
}
}
if (bEqual){
return s;
}
}
return -1;
}
B.KMP算法:
见下面的二,比较重要,也比较难理解,楼主为了方便理解,详细的写在单独的一部分中。
C.BM匹配算法:
BM算法是一种精确字符串匹配算法(区别于模糊匹配)。采用从右向左比较的方法,同时应用到了两种启发式规则,即坏字符规则 和好后缀规则 ,来决定向右跳跃的距离。BM算法的基本流程: 设文本串T,模式串为P。首先将T与P进行左对齐,然后进行从右向左比较。
具体的算法代码见百度百科: 说的比较详细,楼主就不搬来了,链接:https://baike.baidu.com/item/%E6%A8%A1%E5%BC%8F%E5%8C%B9%E9%85%8D/1258334?fr=aladdin
二、KMP算法是什么?
先看看某度的解释。。
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称KMP算法)。KMP算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数,函数本身包含了模式串的局部匹配信息。时间复杂度O(m+n)。
KMP算法的核心,也就是为什么可以如此的高效?关键就在于它Next数组的存在,有了Next数组就好比有一个滑动窗口,这样就避免了在匹配过程的主串中元素下标 i 不会发生回溯,也就是比较过程中的 i 始终是增加或不变的,这样就使得时间复杂度降低了,效率大大提高。
如下例子:主串T为“BABABCAB”,模式串S为“ABCA”。
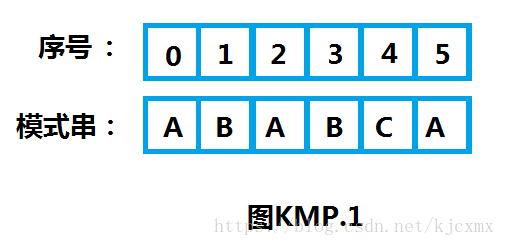
A、见下图KMP.1开始进行Next数组的计算,首先把模式串S进行标号。(下面的例子中下标是从0开始的)
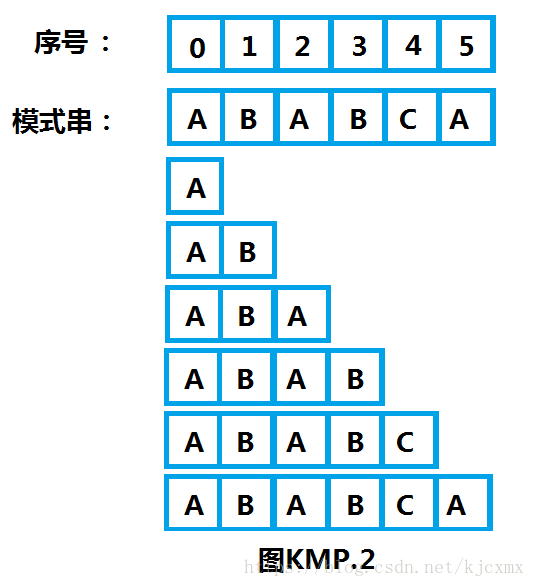
B、见下图KMP.2中,分别写出每个字串的对应前缀,(当然也可以不写出,熟悉之后直接计算即可),最后一行也就是5号“A”对应的前缀为整个模式串。
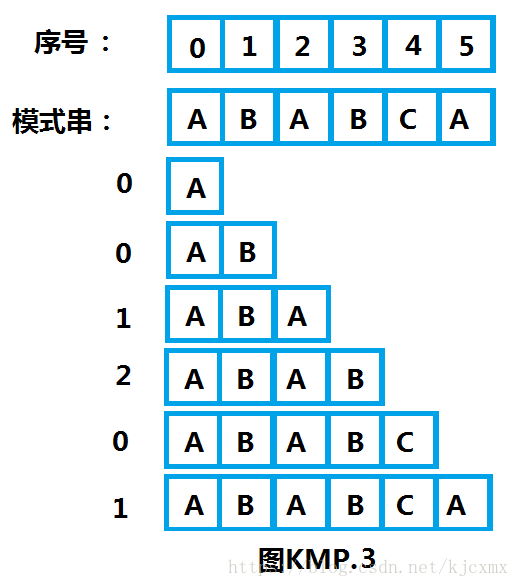
C、见下图KMP.3分别对各个子串的前后缀比较,算出最长字串的长度,写在对应左侧。如下文字分析
第一行,只有一个字符“A”,没有前缀和后缀(前缀和后缀不能为串本身),所以为0
第二行,串为“A B”,前缀为“A”,后缀为“B”,不匹配(一致),所以为0
第三行,串为“A B A”,前缀为“A”和“A B”,后缀为“A”和“B A”,最大匹配长度为“A”=="A",所以为1
第四行,串为“A B A B”,前缀为“A”和“A B”和“ABA”,后缀为“B”和“A B”和“BAB”,最大匹配长度为“A B”=="AB",所以为2
第五行,串为“A B ABC”,前缀为“A”和“A B”和“ABA”和“ABAB”,后缀为“C”和“B ABC”和“ABC”和“BC”均不匹配,所以为0
第六行,串为“A B ABCA”,前缀为“A”和“A B”和“ABA”和“ABAB”和“ABABC”,后缀为“A”和“CA”和“BCA”和“ABCA”和“BABCA”,最大匹配长度为“A”=="A",所以为1
| 子串 | A | AB | ABA | ABAB | ABABC | ABABCA |
| 前缀 | A | A、B、AB | A、AB、ABA | A、AB、ABA、ABAB | A、AB、ABA、ABAB、ABABC | |
| 后缀 | B | B、A、BA | B、AB、BAB | C、BC、ABC、BABC | A、CA、BCA、ABCA、BABCA | |
| 最大 | A、B | AB | A | |||
| 最大长度 | 0 | 0 | 1 | 2 | 0 | 1 |
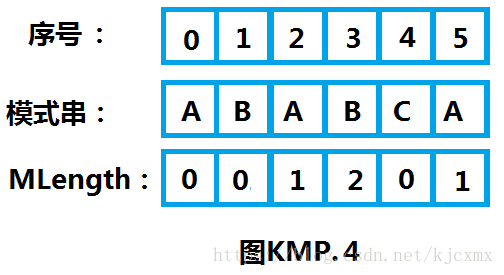
D、见下图KMP.4我们得到了一个数列“001201”,并不是我们的Next数组,把这个数列不妨叫做MLength,对应写在子串下面。
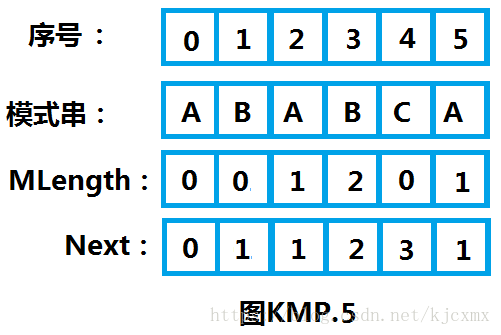
E、见下图KMP.5我们将MLength中最后一个元素即“1”删除,在开头增加一个元素“-1”,然后将整个MLength加一,即得到Next数组“011231”。到此我们便得到了Next数组,下面给出代码
Java代码:
/**
* 获取next数组的值
* @param ps 模式串(匹配串)
* @return
*/
public static int[] getNext(String ps) {
char[] p = ps.toCharArray();
int[] next = new int[p.length];
next[0] = -1;
int j = 0;
int k = -1;
while (j < p.length - 1) {
if (k == -1 || p[j] == p[k]) { //判断是否匹配
next[++j] = ++k;
} else {
k = next[k];
}
}
return next;
}C/C++代码:
void GetNext(char* p,int next[]){
int pLen = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j < pLen - 1) {
if (k == -1 || p[j] == p[k]) { //p[k]表示前缀,p[j]表示后缀
++k;
++j;
next[j] = k;
} else{
k = next[k];
}
}
}
优化KMP算法:
其实上面的方法求Next数组,有一定的缺陷,匹配不成功有时候需要将模式串的j回溯。所以对于已经匹配过的了,就不必再重新回到开头重新匹配了。
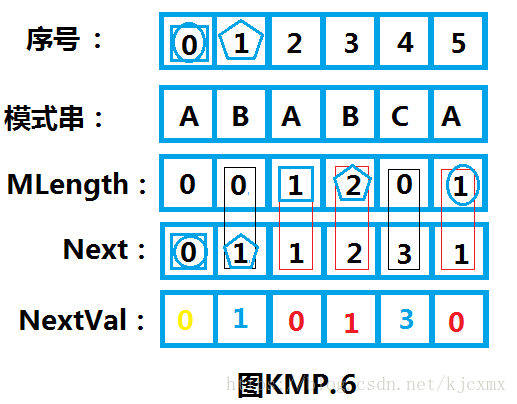
A、见下图KMP.6我们将在图KMP.5中修改,新增一行,分为两步给出NextVal数组。首先将第一个元素填为0
- 如果MLength[j]!=Next[j],则对应的填入Next中的数值
- 如果MLength[j]==Next[j],则对应的填入j-1对应的序号中的Next数值(这句话比较绕,多想想)这里的j是大于1的,即为j>1.这就解释了为什么首元素置零了。图中标的挺清楚,对应的符号一块看。
给出下面代码:
Java代码:
/**
* 优化后的获取next数组的值
* @param ps 模式串(匹配串)
* @return
*/
public static int[] getNextVal(String ps) {
char[] p = ps.toCharArray();
int[] next = new int[p.length];
next[0] = -1;
int j = 0;
int k = -1;
while (j < p.length - 1) {
if (k == -1 || p[j] == p[k]) {
if (p[++j] == p[++k]) { //增加了一层判断,当两个字符相等时要跳过,否则赋值为k
next[j] = next[k];
} else {
next[j] = k;
}
} else {
k = next[k];
}
}
return next;
}C/C++代码:
void GetNextval(char* p, int next[]) {
int pLen = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j < pLen - 1) {
if (k == -1 || p[j] == p[k]) { //p[k]表示前缀,p[j]表示后缀
++j;
++k;
if (p[j] != p[k]) //只需要改动在下面4行,添加一步判断
next[j] = k;
else
next[j] = next[k];
} else {
k = next[k];
}
}
}KMP算法:
Java代码:
/**
* 经典KMP算法
* @param ts 主串(目标串)
* @param ps 模式串(匹配串)
* @return
*/
public static int KMPSearch(String ts, String ps) {
char[] t = ts.toCharArray();
char[] p = ps.toCharArray();
int i = 0; // 主串的位置
int j = 0; // 模式串的位置
int[] next = getNext(ps);
while (i < t.length && j < p.length) { //主要是这个循环
if (j == -1 || t[i] == p[j]) { // 当j为-1时,要移动的是i,j也要归0
i++;
j++;
} else {
// i不需要回溯 i = i - j + 1;
j = next[j]; // j回到指定位置
}
}
if (j == p.length) {
return i - j;
} else {
return -1;
}
}C/C++代码:
int KmpSearch(char* s, char* p) {
int i = 0;
int j = 0;
int sLen = strlen(s);
int pLen = strlen(p);
while (i < sLen && j < pLen) {
if (j == -1 || s[i] == p[j]){//j = -1,或当前字符匹配成功(即S[i]==P[j])则后移
i++;
j++;
} else {
j = next[j];
}
}
if (j == pLen)
return i - j;
else
return -1;
}结语:
这样就完成了著名的KMP算法,算法中重要的是算法所蕴含的思想,理解了具体的算理也就能迁移到其他方面了。