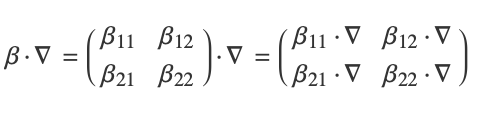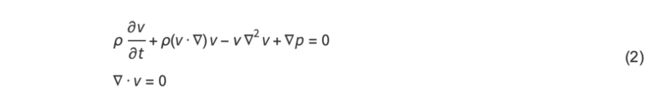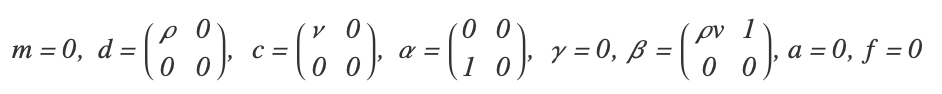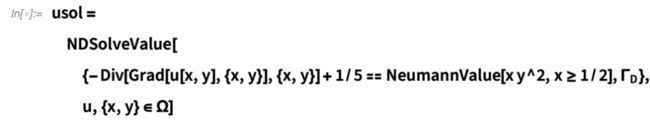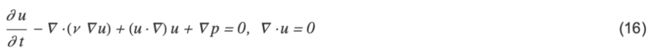Wolfram | 有限元法在非线性偏微分方程中的应用
Mathematica 12¨PDE·°±è§¤§è°é12¨°¨éFEMé§PDE±è§¨éèé¨±è§ PDE Wolfram èè¨èé·èèé°éè·é§ééè Mathematica 12 FEM ±è§è¨°±¤Gray-Scott¨é-¨¤¨Wolfram è訨"é¨"°¤§é¨é¤¨éè§
1. è¨
Wolfram Research è°§ Mathematica éè5000¤§°é±¨ Wolfram è訨°¨/¨éMathematica 12 ·è¤§±è§¨èè·°±è§è鰱觰°è±è§PDEè·/°¨¤°é FEM ¨°12駨±è§éè¨éé騨¨é±è§é§ PDE èè¨è·è§Wolfram è訨"é¨"
2. ¨°±è§è¨
¨ Wolfram è訨è谱觰¤NDSolveNDSolveValue¤è¨è·é¨¤¨è¤¨éè¨è°°¨ "NDSolve"è°è"NDSolveValue" ¨èèè¨ Mathematica ¨ FEMéèè
è°±NDSolve PDE§è¨¨ 2u= 1 ¨ x>=0 u=0 è
è§
2.1 èè¨è
¨NDSolveé¨é¨é·
¤¤±è§é u ¨ Rn°mdaf é± n éc n*n 餤caf± ètx Rnuu m d x 觤éu Rd訨 (1) f d é°éééèè°éé u èèèé/ééè§(u1,,ud)T=(u1,,ud)T
觰·¨¨¤° PDE é (1) ¨¨é¤ m c ¤°é 0 訤éu=(v,p)T R4 NavierStokes ¨
¨¨ (1) 訤
éèèéé°é¤é°éééé°¨ 3 è°èè¨ 4.3 4.4 èè
éè¤ FEM é¨NDSolve¨è§¨ (1) ("Coefficient Form")°è§
è¨(1) c=u,f=4°°è 0 NDSolve PDE èèè
PDE ¨NDSolve§¤èè 2u (x)u (x) è觨 (1) é±èé¨ (1) Coefficient Form è¨ FEM ±è§u(x) èè§u(x) °é°èé°°¨ (1) NDSolveéè¨InactiveèInactivate
![]()
¤ è
2.2
¨°è°¨¤é·éèDiskPolygon±è¨¤¨ParametricRegionImplicitRegion¤¤èéèImageMesh°±§èNDSolve¨°
2.3 è
¨è °éé·è
¤é¨ PDE ¤¤ bc è°predicatef(x,y)=bcéèèè°predicateèTrue°
èèè±NeumannValueè¤éèééé
![]() ¤é§gqu±¨·è·¨NeumannValueDirichletConditionè¨ééèPDE è° §° è·±¨1é §
¤é§gqu±¨·è·¨NeumannValueDirichletConditionè¨ééèPDE è° §° è·±¨1é §![]() é
é
¨è §è§°¨è¤éè¨gqu§¤éNDSolve¤èè
¨u(x,y)=0,x1/2 èx¤0
·u=xy2é·è±è§¨ 2u=0
¨è§PDE èè Coefficient Form¤°èèInactive¨ Inactive[Div], Inactive[Grad]
Divè·è(1) c 1èèè
·cu= ·u=xy2èNeumannValueè§
é許NeumannValue¨(1) PDE ¨ (4) ¤èéè"¨"è°è¨ 2u+1/5=0è·u=xy2(x1/2) é·u(x,y)=0(x¤0)¨NDSolve PDE è 52u+1=0NDSolve (1) è¤c=5 ·cu NeumannValueé 5xy2è·éè¨é·èé PDE è2u+1/5=0 52u+ 1 =0 ¤
è 2u+ 1/5 ==0
è 52u+ 1 ==0
3u+ u=xy2¤NDSolve PDE·§2u+1/5§ 5*NeumannValue[1/2*x*y2 3/2*u[x, y], x1/2]
3. Wolfram èè¨é§é
¨ FEMé訨¤·±è¨èèè訤··è§TriangleTetGenéè§è¨è¨Triangleèè Delaunay è§ Delaunay è§(constrained Delaunay triangulation) éDelaunayè§(conforming Delaunay triangulation)TetGen¨é Delaunay éèDelaunay Wolfram è訰¨éè訨¨èèè¨Triangleèè·§ [4.1] èTetGenèè·è§ [4.2] è
¨§ PDE 觨 PDE ±°±è§è¨±è§é§ PDE¨
¨§éè§éè§é§PDE
§¨èè±è§
§è·è§·¨èè·
¨è·è§°§è°1§·
°±èé訨 Newton-Raphson ±è§é§°¨è¨¨é° Wolfram ¨è
éé¤(1) é°é¨
![]()
è°
![]()
°°é§ PDE è觱 1 é駨°è§°°u0§±¤èéè2·(u)F(u)=0 è§u¤uu0é·r=uu0
°F¨u0¨éè°±O(r2) ééé
' F' ±éèè /u/uF/uF/u¨u0¤±(9) è u 觨¨èééèè§èè°éè¨ r
§u0éè¤u(x)=0, xNDSolveéé InitialSeeding{u[x,y]==x+Exp[-Abs[y]]} èè°§èè§èè°±é¨è§é駨¤(13)è· r ·§°éé ·'(u0)F'(u0) è餧褧°±è館 Wolfram èè¨¨é§ FEM °¨°éAffine Covariant Newton Newton-Raphson ¨èè館éèè°éè°
é§éèéè·¨é°é¨è¨§è° (Method of lines)[5]¨° FEM ¨é
4. ¨
4.1 é§
¨§ ±¨é觷é§èé°¤èèè¨éé![]()
 °¨è·¨è
°¨è·¨è
è¨z·éééèé x yé°è¨ z °±¤¨(10) z éé u=Az PDE
(B)¨é°¨
¤¨¨é¤è¨éèè騱¨éèé§ PDE (11)èèè
è觨NDSolveéé·è¨¤é¨é
°è·è·¤
4.2 鱨èéé
è°¨ Navier-Stokes ¨
é¨é騤= 1 ¤é駤¤± u 騱¤¨uxuy¨è¨è·è§éèèèééé·¨è§éux鱨°§§ééé·è§éWolfram èè¨
è§è·é
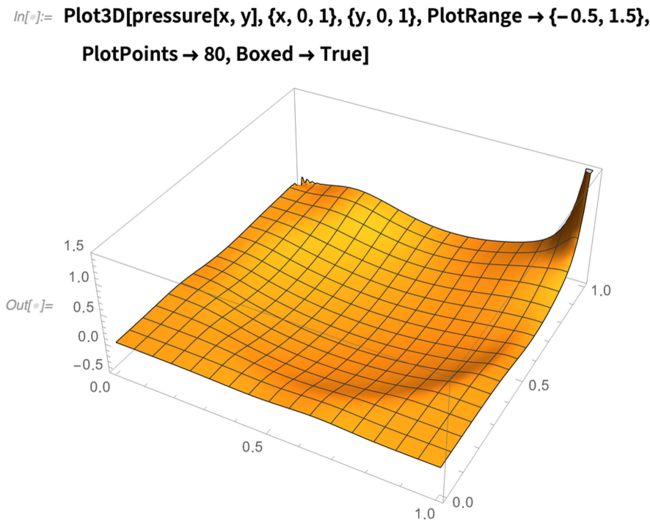
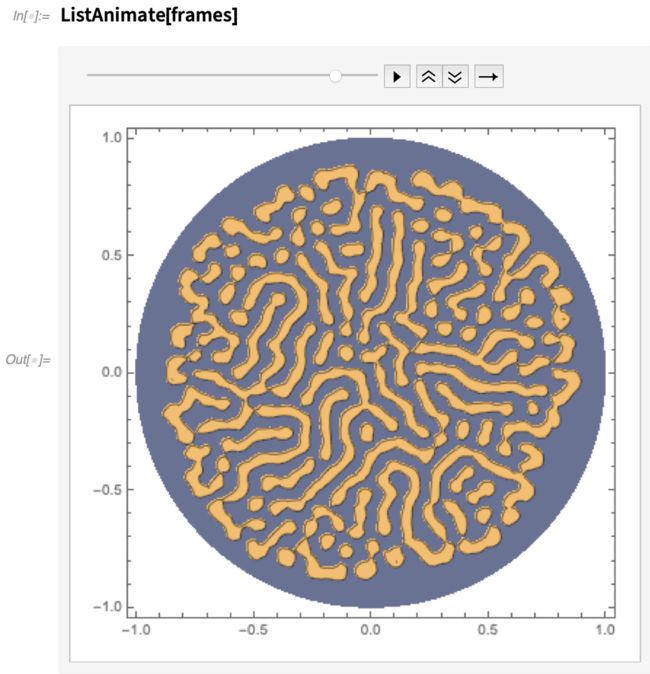
4.3 Gray-Scott ¨
±è¨è褧è¨è§°¤¨èé§è PDEGray-Scott ¨¤¤é¨°è¨ U è°§è¨ V ¨èèè
U § P° P °¤é¨U V u v ééè°°±è¨
DuDvè°Fè¨ U èKé VP °èè¨è°è§¨¤
4.4 ±¨
éè°ééé·°(12)è°éé¨
¨¤éèé¨èèéé±èéé°é(u,v) p±é xy éWolfram èè¨
Navier-Stokes ¨
褰±¤§°érampFunctionè°éé¨ééé鱤§°é¤¤é·è° 200
è§
é t = 0 ° 10 ±NDSolve¨è§ t è¨é PC (3.1GHz Intel Core i516GB) ¤§éèè 6 é
éèèè¨
è¤è
5. è
Mathematica 12Wolframèè¨ 12¤§°±é¨è Navier-Stokes ¨¨è¤é§¨±è§è± Wolfram è訨·èéè PDE é¨è±è§é§§èé騧 FEM 騤跤Mathematica ¨§°/¨¨è¤é¨è褧è
訷·
é¨https://reference.wolfram.com/language/FEMDocumentation/tutorial/FiniteElementProgramming.html
è§
https://www.cs.cmu.edu/~quake/triangle.html
http://wias-berlin.de/software/index.jsp?id=TetGen
§°èé
èwww.cogitosoft.com
è°è·cogitosoftware
èè
éè+8601068421378
18610247936 QQ368531638
![]()