霍夫变换(Hough Transform):霍夫变化在图像处理以及点云处理中的直线检测应用
霍夫变换(Hough Transfrom)是图像处理中的一种特征提取技术,它通过一种投票算法检测具有特定形状的物体,该过程在一个参数空间中通过计算累计结果的局部最大值得到一个符合该特定形状的集合作为霍夫变换的结果。
最初的霍夫变换是设计用来检测直线和曲线的,起初的方法要求知道物体边界线的解析方程,但不需要有关区域位置的先验知识,这种方法的一个突出优点是分割结果的鲁棒性,即对数据的不完全或者噪声不是非常的敏感,然而要获得描述边界的解析表达常常是不可能的;后经过推广,经典霍夫变换用来检测图像中的直线,再后来霍夫变换扩展到任意形状物体的识别,多为圆或者椭圆。霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或者直线映射到另一个坐标空间的一个点上形成峰值,从而把检测任意形状的问题转化为统计峰值问题。
霍夫变换在OpenCV中分为霍夫线变换和霍夫圆变换两种。
--------------OpenCV中的霍夫线变换
(1)对于直角坐标系中的任意一点A![]() ,经过点A的直线满足
,经过点A的直线满足![]() .(k是斜率,b是截距)
.(k是斜率,b是截距)
为什么要用极坐标而不是笛卡尔坐标呢,(为什么要用极坐标式而不直接用一般形式:ax+by=c(归一化可以去掉参数c),或者其他的如斜截式、截距式呢?首先它们都会遇到奇异情况,比如c=0,斜率=无穷大,其中一个截距=0;再一个是某些形式的参数空间不是闭的,比如斜截式的斜率k,取值范围从0到无穷大,给量化搜索带来了困难。而极坐标式就妙在距离和角度两个参数都是有界的,而且正余弦函数也有界不会发生奇异情况。)本篇博客给了解释:
https://blog.csdn.net/cy513/article/details/4269340
(2)那么在X-Y平面过点A![]() 的直线簇可以用
的直线簇可以用![]() 表示,但对于垂直于X轴的直线斜率是无穷大的则无法表示。因此将直角坐标系转换到极坐标系就能解决该特殊情况。在极坐标中表示:
表示,但对于垂直于X轴的直线斜率是无穷大的则无法表示。因此将直角坐标系转换到极坐标系就能解决该特殊情况。在极坐标中表示:![]() (其中r表示为原点到直线的距离)
(其中r表示为原点到直线的距离)
(3)在极坐标系中表示直线的方程为![]() (r为原点到直线的距离,
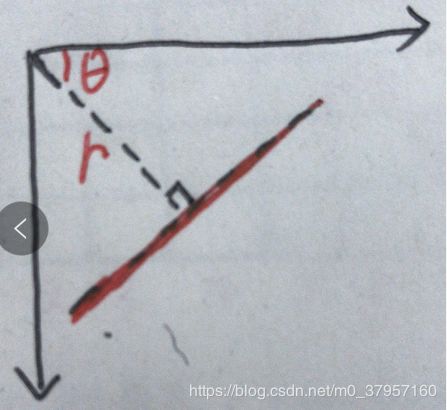
(r为原点到直线的距离,![]() 由该垂直线和水平轴形成的角度以逆时针方向测量(该方向随您如何表示坐标系而变化。此表示形式在OpenCV中使用)。),如左图所示:
由该垂直线和水平轴形成的角度以逆时针方向测量(该方向随您如何表示坐标系而变化。此表示形式在OpenCV中使用)。),如左图所示:
(如左图所示)如果线在原点下方通过,则它将具有正的r且![]() 角度小于180。如果线在原点上方,则将角度取为小于180,而不是大于180的角度。r取负值。任何垂直线将具有0度,水平线将具有90度。
角度小于180。如果线在原点上方,则将角度取为小于180,而不是大于180的角度。r取负值。任何垂直线将具有0度,水平线将具有90度。
现在,让我们看一下霍夫变换如何处理线条。任何一条线都可以用![]() 这两个术语表示。因此,首先创建2D数组或累加器(以保存两个参数的值),并将其初始设置为0。让行表示r,列表示θ。阵列的大小取决于所需的精度。假设您希望角度的精度为1度,则需要180列。对于r,最大距离可能是图像的对角线长度。因此,以一个像素精度为准,行数可以是图像的对角线长度。
这两个术语表示。因此,首先创建2D数组或累加器(以保存两个参数的值),并将其初始设置为0。让行表示r,列表示θ。阵列的大小取决于所需的精度。假设您希望角度的精度为1度,则需要180列。对于r,最大距离可能是图像的对角线长度。因此,以一个像素精度为准,行数可以是图像的对角线长度。
考虑一个8x8的图像,中间有一条水平线。取直线的第一点。您知道它的(x,y)值,(该点所在空间此处称为图像空间,因为我们是在做图像处理,这些点都对应于图像的像素)。现在在线性方程式中,(实际上可以将值θ= 0,1,2,..... 180放进去,然后检查得到r。对于每对(r,θ),在累加器中对应的(r,θ)单元格将值增加1),此处为了方便展示将![]() 划分为45度为一个间隔。所以现在第一次在累加器中,单元格
划分为45度为一个间隔。所以现在第一次在累加器中,单元格![]() 即累加1次。
即累加1次。
现在,对第二个点。执行与上述相同的操作。递增![]() 对应的单元格中的值。这次,单元格
对应的单元格中的值。这次,单元格![]() 。实际上,您正在对(r,θ)值进行投票。您对线路上的每个点都继续执行此过程。在每个点上,单元格
。实际上,您正在对(r,θ)值进行投票。您对线路上的每个点都继续执行此过程。在每个点上,单元格![]() 都会增加或投票,而其他单元格可能会或可能不会投票。这样一来,最后,单元格
都会增加或投票,而其他单元格可能会或可能不会投票。这样一来,最后,单元格![]() 的投票数将最高。因此,如果您在累加器中搜索最大票数,则将获得
的投票数将最高。因此,如果您在累加器中搜索最大票数,则将获得![]() 值,该值表示该图像中的一条线与原点的距离为
值,该值表示该图像中的一条线与原点的距离为![]() ,角度为45度。详细计算过程如下:
,角度为45度。详细计算过程如下:
(4)如上右图,假定在一个8*8的平面像素中有一条直线,并且从左上角(1,8)像素点开始分别计算θ为0°、45°、90°、135°、180°时的r,图中可以看出r分别为1、![]() 、8、
、8、![]() 、-1,并给这5个值分别记一票,同理计算像素点(3,6)点θ为0°、45°、90°、135°、180°时的r,再给计算出来的5个r值分别记一票,此时就会发现
、-1,并给这5个值分别记一票,同理计算像素点(3,6)点θ为0°、45°、90°、135°、180°时的r,再给计算出来的5个r值分别记一票,此时就会发现 ![]() 的这个值已经记了两票了,以此类推,遍历完整个8*8的像素空间的时候
的这个值已经记了两票了,以此类推,遍历完整个8*8的像素空间的时候![]() 就记了5票, 别的r值的票数均小于5票,所以得到该直线在这个8*8的像素坐标中的极坐标方程为
就记了5票, 别的r值的票数均小于5票,所以得到该直线在这个8*8的像素坐标中的极坐标方程为 ![]() ,到此该直线方程就求出来了。(PS:但实际中θ的取值不会跨度这么大,一般是1度)。
,到此该直线方程就求出来了。(PS:但实际中θ的取值不会跨度这么大,一般是1度)。
投票机制:
对于笛卡尔坐标系即直角坐标系给定的一个定点![]() ,我们在极坐标对极径极角平面汇出所有通过他的直线,将得到一条正弦曲线,例如对于给定点
,我们在极坐标对极径极角平面汇出所有通过他的直线,将得到一条正弦曲线,例如对于给定点![]() 和
和![]() 可以绘出如下所示的平面图:(图中只绘制出了满足
可以绘出如下所示的平面图:(图中只绘制出了满足![]() 和
和![]() )
)
(所以我们可以得到一个结论,给定平面中的单个点,那么通过该点的所有直线的集合对应于 (ρ, θ) 平面中的一条正弦曲线。)
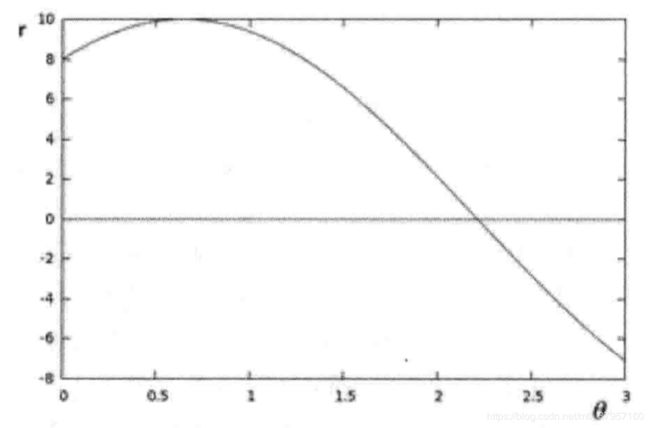 绘制出的正弦曲线
绘制出的正弦曲线
之后可以按照上述步骤对图像中所有的点进行上述操作,如果两个不同点进行上述操作后得到的曲线在平面![]() 相交,这就意味着这两个点通过同一条直线,例如在上图中继续对点
相交,这就意味着这两个点通过同一条直线,例如在上图中继续对点![]() 和点
和点![]() 绘图,得到如下图:(实际中可以将图像空间上所有对应的点在参数空间上的直线都画出来)
绘图,得到如下图:(实际中可以将图像空间上所有对应的点在参数空间上的直线都画出来)
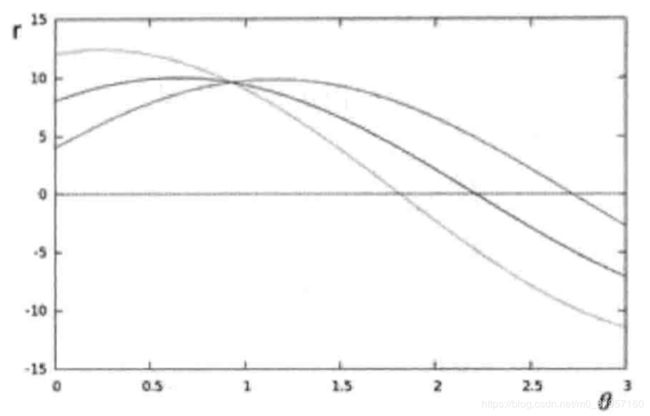 绘制出的曲线
绘制出的曲线
从上图可以看出这三条曲线在极坐标平面相交于点(0.925,9.6)该坐标表示的是![]() ;或者可以说在极坐标下的该点(0.925,9.6)表示平面内的一条直线,即直角坐标系下
;或者可以说在极坐标下的该点(0.925,9.6)表示平面内的一条直线,即直角坐标系下![]() 这三点组成的直角坐标系下平面内的直线。
这三点组成的直角坐标系下平面内的直线。
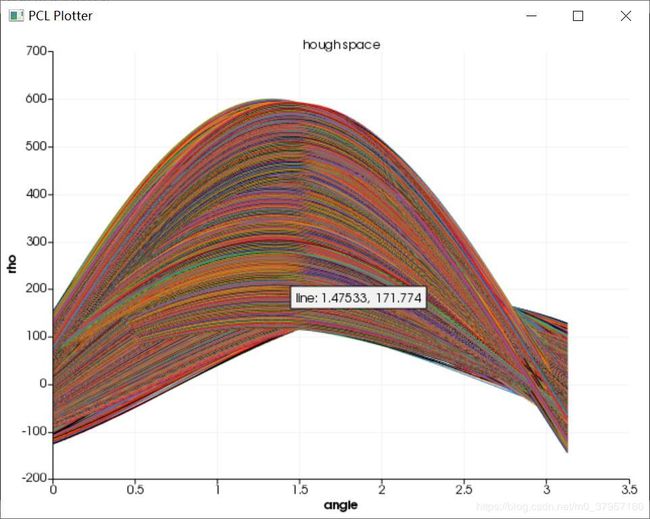
从霍夫空间曲线图来看,取不同的像素点都汇聚在一个点(上述取不同的像素点都汇聚在![]() ,这表明这些个像素点都属于同一条直线。(xi,yi)对于任意一条直线上的所有点来说变换到极坐标中,从[0~360]空间,可以得到r的大小属于同一条直线上点在极坐标空(r, θ)必然在一个点上有最强的信号出现(如上图),根据此反算到平面坐标中就可以得到直线上各点的像素坐标。从而得到直线。
,这表明这些个像素点都属于同一条直线。(xi,yi)对于任意一条直线上的所有点来说变换到极坐标中,从[0~360]空间,可以得到r的大小属于同一条直线上点在极坐标空(r, θ)必然在一个点上有最强的信号出现(如上图),根据此反算到平面坐标中就可以得到直线上各点的像素坐标。从而得到直线。
参考博客:https://blog.csdn.net/yuyuntan/article/details/80141392
https://blog.csdn.net/shanchuan2012/article/details/74010561
算法实现:
- 读取原始图并转换成灰度图,采用边缘检测算子(如Canny)转换成二值化边缘图像;
- 对该图像进行霍夫变换;
- 找到大于阈值的累加器,和对应的 ρ, θ 参数。
更详细的算法描述:
1.读取原始图并转换成灰度图,采用边缘检测算子(如Canny)转换成二值化边缘图像。
2.然后对该图像进行霍夫变换。
3.先使用峰值检测函数,找到大于阈值的霍夫变换单元(局部最大值应该最可能是线,步长和量化会影响效果)。
4.将上述识别出的一组候选峰,需要确定与其相关的线段及其起始点和终止点(这需要一定的算法,很多论文对此都做了改进,诸如蝴蝶形状宽度,峰值走廊)。
5.然后描绘于原图(或结果图)上。
用刚才的方法,找到的都是直线;而我们在实际应用中,可能更关心线段的提取。这就需要概率霍夫变换(Probabilistic Hough Transform)
以上讲解表明,一般来说一条直线能够通过在极坐标平面![]() 寻找交于一点的曲线数量来检测,而越多曲线交于一点也就意味着这个交点表示的直线由更多的点组成,一般来说我们可以通过设置直线上点的阈值来定义多少条曲线交于一点,这样才认为检测到了一条直线。这就是霍夫变换要做的,他追踪图像中每个点对应曲线中的交点,如果交于一点的曲线的数量超过了阈值,那么可以认为这个交点所代表的参数对
寻找交于一点的曲线数量来检测,而越多曲线交于一点也就意味着这个交点表示的直线由更多的点组成,一般来说我们可以通过设置直线上点的阈值来定义多少条曲线交于一点,这样才认为检测到了一条直线。这就是霍夫变换要做的,他追踪图像中每个点对应曲线中的交点,如果交于一点的曲线的数量超过了阈值,那么可以认为这个交点所代表的参数对![]() 在原图像中为一条直线。
在原图像中为一条直线。
标转霍夫变换函数解读:
void HoughLine(InputArray image, OutputArray lines, double rho, double theta, int threshold, double srn=0, double stn=0)第一个参数:InputArray类型的image,输入图像,即源图像,要求为8位的单通道二进制图像,可以将任意的原图载入进来,并由函数修改成此格式后再填进这里。
第二个参数:OutputArray类型的lines,经过调用HoughLines函数后存储了霍夫线变换检测到线条的的输出适量。每一条线由具有两个元素的矢量![]() 表示,其中r是离坐标原点(0,0)也就是图像的左上角的剧,
表示,其中r是离坐标原点(0,0)也就是图像的左上角的剧,![]() 是弧度线条旋转角度(0度表示垂直线,
是弧度线条旋转角度(0度表示垂直线,![]() Π/2度表示水平线)。
Π/2度表示水平线)。
第三个参数:
第四个参数:
第五个参数:
第六个参数:
第七个参数:
第三个参数,double类型的rho,以像素为单位的距离精度。另一种形容方式是直线搜索时的进步尺寸的单位半径。PS:Latex中/rho就表示 。第四个参数,double类型的theta,以弧度为单位的角度精度。另一种形容方式是直线搜索时的进步尺寸的单位角度。第五个参数,int类型的threshold,累加平面的阈值参数,即识别某部分为图中的一条直线时它在累加平面中必须达到的值。大于阈值threshold的线段才可以被检测通过并返回到结果中。第六个参数,double类型的srn,有默认值0。对于多尺度的霍夫变换,这是第三个参数进步尺寸rho的除数距离。粗略的累加器进步尺寸直接是第三个参数rho,而精确的累加器进步尺寸为rho/srn。第七个参数,double类型的stn,有默认值0,对于多尺度霍夫变换,srn表示第四个参数进步尺寸的单位角度theta的除数距离。且如果srn和stn同时为0,就表示使用经典的霍夫变换。否则,这两个参数应该都为正数。
//-----------------------------------【头文件包含部分】-----------------------------------
// 描述:包含程序所依赖的头文件
#include
#include
//-----------------------------------【命名空间声明部分】----------------------------------
// 描述:包含程序所使用的命名空间
using namespace cv;
//-----------------------------------【main( )函数】-------------------------------------
// 描述:控制台应用程序的入口函数,我们的程序从这里开始
int main()
{
//【1】载入原始图和Mat变量定义
Mat srcImage = imread("1.jpg"); //工程目录下应该有一张名为1.jpg的素材图
Mat midImage, dstImage;//临时变量和目标图的定义
//【2】进行边缘检测和转化为灰度图
Canny(srcImage, midImage, 50, 200, 3);//进行一此canny边缘检测
cvtColor(midImage, dstImage, CV_GRAY2BGR);//转化边缘检测后的图为灰度图
//【3】进行霍夫线变换
vector lines;//定义一个矢量结构lines用于存放得到的线段矢量集合
HoughLines(midImage, lines, 1, CV_PI / 180, 150, 0, 0);
//【4】依次在图中绘制出每条线段
for (size_t i = 0; i < lines.size(); i++)
{
float rho = lines[i][0], theta = lines[i][1];
Point pt1, pt2;
double a = cos(theta), b = sin(theta);
double x0 = a*rho, y0 = b*rho;
pt1.x = cvRound(x0 + 1000 * (-b));
pt1.y = cvRound(y0 + 1000 * (a));
pt2.x = cvRound(x0 - 1000 * (-b));
pt2.y = cvRound(y0 - 1000 * (a));
line(dstImage, pt1, pt2, Scalar(55, 100, 195), 1, CV_AA);
}
//【5】显示原始图
imshow("【原始图】", srcImage);
//【6】边缘检测后的图
imshow("【边缘检测后的图】", midImage);
//【7】显示效果图
imshow("【效果图】", dstImage);
waitKey(0);
return 0;
}
---------------------点云数据中的霍夫变换检测直线:
由上边的介绍我们知道在二维平面内直线的表达形式为:![]() (此式中k,b已知;x,y未知,可以确定一条直线)
(此式中k,b已知;x,y未知,可以确定一条直线)
对应的极坐标下的形式(即霍夫空间)为:![]() (此式中x,y已知,ρ,θ未知;)(多个(ρ,θ)对可以确定一条线,所以如果知道了多条线即多个(x,y)在极坐标下确定得曲线交与同一个ρθ,那么这个交点(ρ,θ)对在笛卡尔坐标系中对应于一条直线)
(此式中x,y已知,ρ,θ未知;)(多个(ρ,θ)对可以确定一条线,所以如果知道了多条线即多个(x,y)在极坐标下确定得曲线交与同一个ρθ,那么这个交点(ρ,θ)对在笛卡尔坐标系中对应于一条直线)
所以弄清楚以上原理我们就可以将霍夫直线检测运用到点云数据中。(霍夫变换是将点变换到霍夫空间,然后离散化霍夫空间形成累加器计算累积的数目,Pick一个峰值点。)
首先要实现的目的是:在XOY平面内,检测混有噪声的点云数据中的直线。
具体思路:
(1)前期根据自己需要,是否需要对点云进行滤波降采样处理;(滤波是为了找到自己感兴趣区域,降采样是为了减少点数)
(2)将三维点云数据投影到二维平面内(此处是XOY平面内)
(3)将点云在二维平面内画规则格网,横轴为角度θ,纵轴为长度ρ,设定步长(就是横纵坐标的间隔划分),我取了横轴1度一个步长,纵轴0.5米为一个步长,将点云从![]() 空间按照公式
空间按照公式![]() 转换到霍夫空间。
转换到霍夫空间。
(4)在霍夫空间中观察交点个数即就是求交点的过程,因为通常情况下,点为离散点,不可能完全交于一个点,所以,此处使用局部极大值点代替,即需要求局部极值大点。(在霍夫空间中有几个交点,即有几个极大值点说明对应的欧式空间下就有几条直线)
PS:求极值的方法:
求解每个点、每个角度步长对应的长度值,算一下它分属于哪一个格网,(即将欧氏空间下点的坐标换算到霍夫空间下求一下换算后的ρ和θ,再计算一下它属于我们划分的霍夫空间下的规则格网下边的哪个格子)将所有点进行计算,对格网内数值进行累加(到最后平均数即为该交点的长度值,即rho值),对每个格网进行计数,如果存在格网内点数量比邻域8格网内的点数量都多,我们认为他是极值点。
但是,会发现其实极值点的数还是挺多的,远不止五个,所以还需要加入另一个阈值,格网内的最小点数,大于它才能判断为极值点。
所以,这个参数其实挺难确定的,如果事先知道有几条直线,就省事了—所以,选择了两种方式进行计算(1.指定格网最小数量阈值,2,指定格网最小数量阈值和直线个数阈值),看到底符合哪个需求了-----
代码部分:
HOUGH_LINE.h:
//HOUGH_LINE.h文件
#pragma once
#include
#include
#include
#include
#include
#include
#include
#include
using namespace pcl;
using namespace Eigen;
using namespace std;
typedef PointXYZ PointT;//定义一种新的数据类型
class HOUGH_LINE//类
{
public:
HOUGH_LINE();
~HOUGH_LINE();//析构函数
template void vector_sort(std::vector vector_input, std::vector &idx);//函数模板
inline void setinputpoint(PointCloud::Ptr point_);//内联函数
void VoxelGrid_(float size_, PointCloud::Ptr &voxel_cloud);//降采样
void draw_hough_spacing();//自定义函数
void HOUGH_line(int x_setp_num, double y_resolution, int grid_point_number_threshold, vector&K_, vector&B_, int line_num = -1);//自定义函数
void draw_hough_line();//自定义函数
private:
PointCloud::Ptr cloud;
int point_num;//点数
PointT point_min;//最小点数量
PointT point_max;//最大点数量
vector>result_;//vector容器
};
//函数模板:函数模板的重点是模板。表示的是一个模板,专门用来生产函数。//模板函数:是函数模板的实例化,是一个函数。
templatevoid//定义上边的vector_sort()函数
HOUGH_LINE::vector_sort(std::vector vector_input, std::vector &idx) //&idx引用//vector( T 表示存储元素的类型)此处不限制类型,vector 实现的是一个动态数组,即可以进行元素的插入和删除,在此过程中,vector 会动态调整所占用的内存空间,整个过程无需人工干预
{
idx.resize(vector_input.size());
iota(idx.begin(), idx.end(), 0);//初始为0,进行自增
sort(idx.begin(), idx.end(), [&vector_input](size_t i1, size_t i2) { return vector_input[i1] > vector_input[i2]; });//排序函数,按照指定的规则对[begin, end)按照从大到小排序,其中第三个参数使用到lambda表达式C++11中新增准则
}
inline void HOUGH_LINE::setinputpoint(PointCloud::Ptr point_) //定义上边的内联函数setinputpoint()
{
cloud = point_;
point_num = cloud->size();
}
HOUGH_LINE.cpp
见链接:https://download.csdn.net/download/m0_37957160/12561010
主函数main.cpp
//主函数,调用
#include "HOUGH_LINE.h"
int main()
{
PointCloud::Ptr cloud(new PointCloud);
pcl::io::loadPCDFile("F:\\coutsaved\\test\\warehouse\\1.pcd", *cloud);
PointCloud::Ptr VOXEL;
HOUGH_LINE hough;
hough.setinputpoint(cloud);
hough.VoxelGrid_(1.0, VOXEL);
hough.draw_hough_spacing();
vectorK_, B_;
hough.HOUGH_line(181, 0.5, 400, K_, B_);//按阈值自动检测
//hough.HOUGH_line(181, 0.5, 400, K_, B_, 3);//指定只选择极大值最大的3条直线
hough.HOUGH_line(181, 0.5, 400, K_, B_, 5);//指定只选择极大值最大的3条直线
hough.draw_hough_line();
return 0;
}
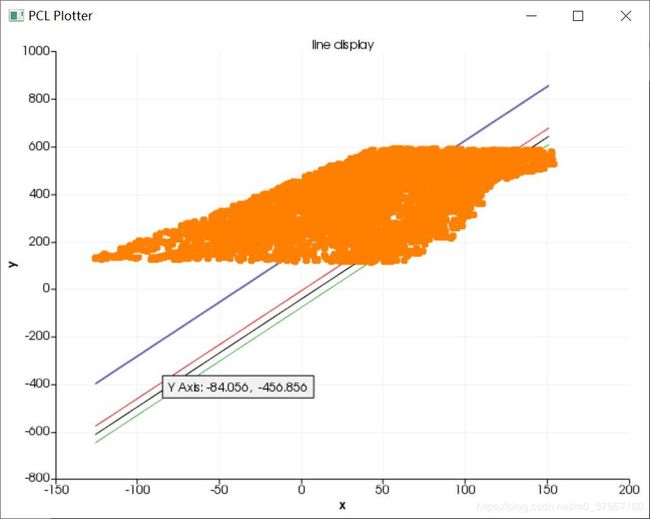
先贴一下程序执行的效果:
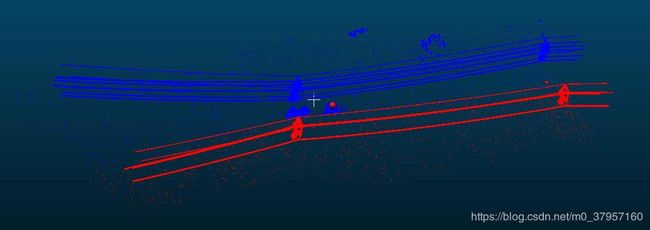
原始点云数据:
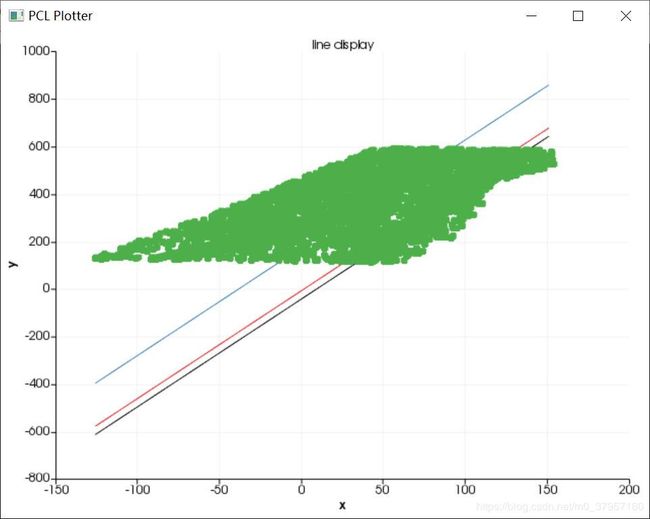
按照不同的阈值检测不同数量的直线效果:
下图对应于代码中的邻域查找:
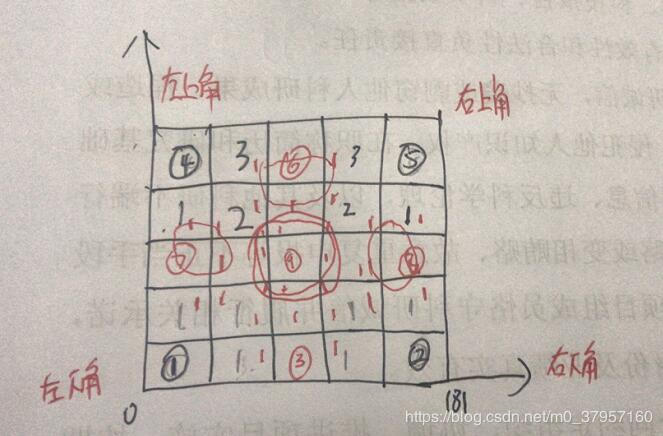 邻域查找解释图
邻域查找解释图