几道二分查找法案例

一）搜索所有和key相等的数

题目：在一个有序列表中，搜索所有和key相等的数。

步骤：

第一步：先按二分查找法的方式，判断key是否存在数据中，如存在就继续下一步，否则返回null。

第二步：从数据中查找到key的下标位置，因为数据是有序的，声明左右两个临时指针low和high，以key的下标位置为中心，分别向左右两个方向探测，比较是否还有和key相同的元素。

第三步：围绕key下标位置探测到的元素就是和key相等的元素，区间是low到high。

源码：

/**
 * 在一个有序列表中，搜索所有和key相等的数。
 */
public static int[] findeqKey(int[] nums, int key) {
	if (nums == null) {
		return null;
	}
		
	int low = 0;
	int high = nums.length-1;
		
	while (low <= high) {
		int mid = (low + high) >>> 1;
			
		if (nums[mid] < key) {
			low = mid + 1;
		} else if (nums[mid] > key) {
			high = mid - 1;
		} else {
			// 需要先找到和key相等的数,然后围绕mid左右探测
			low = mid;
			high = mid;
				
			// 往low方向探测
			while (low > 0 && nums[low] == nums[low-1]) {
				low--;
			}
				
			// 往high方向探测
			while (high < nums.length-1 && nums[high] == nums[high+1]) {
				high++;
			}
				
			// low致high之间的元素就是所有和key相同的数
			return Arrays.copyOfRange(nums, low, high + 1);
		}
	}
	return null;
}

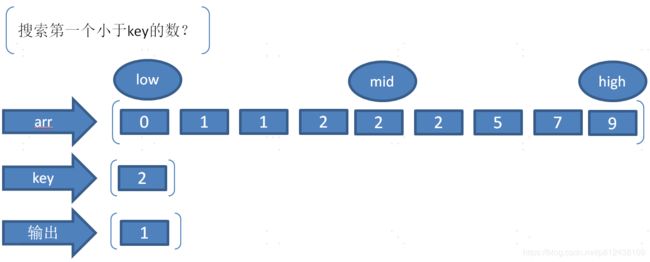
二）搜索第一个小于key的数

题目：在一个有序列表中，搜索第一个小于key的数。

步骤：

第一步：先按二分查找法的方式，判断key是否存在数据中，如存在就继续下一步，否则返回null。

第二步：从数据中查找到key的下标位置，因为数据是有序的，比key小的元素都会排列再左侧，从右往左方向探测，直到找到第一个比key小的元素为止。

源码：

/**
 * 在一个有序列表中，搜索第一个小于key的数
 */
public static int findltKey(int[] nums, int key) {
	if (nums == null) {
		return -1;
	}
		
	int low = 0;
	int high = nums.length-1;
		
	while (low <= high) {
		int mid = (low + high) >>> 1;
			
		if (nums[mid] < key) {
			low = mid + 1;
		} else if (nums[mid] > key) {
			high = mid - 1;
		} else {
			// 需要先找到和key相同的数，比key小的数就是从mid往low方向找
			while (mid > 0 && nums[mid] == nums[mid-1]) {
				mid--;
			}
			if (mid <= 0) { // 需考虑第一位就和key相同的情况
				break;
			}
			return nums[mid-1];
		}
	}
		
	return -1;
}

三）搜索第一个大于key的数

题目：在一个有序列表中，搜索第一个大于key的数

步骤：

第一步：先按二分查找法的方式，判断key是否存在数据中，如存在就继续下一步，否则返回null。

第二步：从数据中查找到key的下标位置，因为数据是有序的，比key大的元素都会排列再右侧，从左往右方向探测，直到找到第一个比key大的元素为止。

源码：

/**
 * 在一个有序列表中，搜索第一个大于key的数
 */
public static int findgtKey(int[] nums, int key) {
	if (nums == null) {
		return -1;
	}
		
	int low = 0;
	int high = nums.length-1;
		
	while (low <= high) {
		int mid = (low + high) >>> 1;
			
		if (nums[mid] < key) {
			low = mid + 1;
		} else if (nums[mid] > key) {
			high = mid - 1;
		} else {
			// 需要先找到和key相同的数，比key大的数就是从mid往high方向找
			while (mid < nums.length-1 && nums[mid] == nums[mid+1]) {
				mid++;
			}
			if (mid >= nums.length-1) { // 需考虑最后一位就和key相同的情况
				break;
			}
			return nums[mid+1];
		}
	}
		
	return -1;
}

识别二维码关注个人微信公众号

本章完结，待续，欢迎转载！
 
本文说明：该文章属于原创，如需转载，请标明文章转载来源！