【ALGO】组合数学(2)
文章导航
- 前文链接
- Lucas定理
- Catalan数列
- 乘法逆元
- 例题
- ACW 1309. 车的放置
- 题面
- 解析
- AC代码
- CQOI 2014. 数三角形
- 题面
- 解析
- AC代码
- BZOJ 4403. 序列统计
- 题面
- 解析
- AC代码
前文链接
组合数学(1)
Lucas定理
若 p p p是质数,则对于任意整数 1 ≤ m ≤ n 1\leq m \leq n 1≤m≤n,有以下关系成立
C n m = C n m o d p m m o d p × C n / p m / p ( m o d p ) C_n^m=C_{n \bmod{p}}^{m\bmod{p}}\times C_{n/p}^{m/p}\pmod{p} Cnm=Cnmodpmmodp×Cn/pm/p(modp)
Catalan数列
给定 n n n个0和 n n n个1,按照某种顺序排成长度为 2 n 2n 2n的序列,满足任意前缀中0的个数都不少于1的个数的序列数量为:
h ( n ) = C 2 n n n + 1 h(n)=\frac{C_{2n}^n}{n+1} h(n)=n+1C2nn
并且满足递推公式
h ( n ) = h ( n − 1 ) × 4 n − 2 n + 1 h(n)=h(n-1)\times \frac{4n-2}{n+1} h(n)=h(n−1)×n+14n−2
与Catalan数有关的问题
- n n n个左括号和 n n n个右括号组成的合法括号序列数量为 h ( n ) h(n) h(n)
- 1 , 2 , … , n 1,2,\dots, n 1,2,…,n经过一个栈,形成合法的栈序列为 h ( n ) h(n) h(n)
- n n n个节点构成不同的二叉树的数量为 h ( n ) h(n) h(n)
- 在平面直角坐标系上,每一步只能向上或者向右走,从 ( 0 , 0 ) (0, 0) (0,0)走到 ( n , n ) (n, n) (n,n)并且除两个端点外不接触直线 y = x y=x y=x的路线数量为 2 h ( n ) 2h(n) 2h(n)
乘法逆元
若整数 b , p b, p b,p互质,并且 b ∣ p b\mid p b∣p,则存在一个整数 x x x,使得 a b ≡ a ∗ x ( m o d p ) \frac{a}{b}\equiv a*x\pmod{p} ba≡a∗x(modp),称 x x x为 b b b的模 p p p乘法逆元,记为 b − 1 ( m o d p ) b^{-1}\pmod{p} b−1(modp). b<p
如果 p p p为质数,并且 b < p b
例题
ACW 1309. 车的放置
题目链接
题面
在图示参数为 a , b , c , d a, b, c, d a,b,c,d的网格棋盘中,放上 K K K个相互不攻击的车,求方案的总数
解析
将棋盘做如图所示的切分
 枚举在左上部分摆 i i i个车,在下半部分摆 K − i K-i K−i个车,进行组合计数,可以推出方案总数为
枚举在左上部分摆 i i i个车,在下半部分摆 K − i K-i K−i个车,进行组合计数,可以推出方案总数为
∑ i = 0 k C b i P a i C a k − i P a + c − i k − i \sum_{i=0}^kC_b^iP_a^iC_a^{k-i}P_{a+c-i}^{k-i} i=0∑kCbiPaiCak−iPa+c−ik−i
AC代码
#include CQOI 2014. 数三角形
题目链接
题面
在一个 n × m n\times m n×m的网格,计算三个点都在格点上的三角形的数量
解析
分情况进行组合计数,考虑三点共线不能组成三角形的情况
- 斜率为 0 0 0: n × C m 3 n\times C_m^3 n×Cm3
- 斜率为 ∞ \infty ∞: m × C n 3 m\times C_n^3 m×Cn3
- 斜率为非 0 0 0实数: ∑ i ≤ i ≤ n ∑ 1 ≤ j ≤ n ( gcd ( i , j ) − 1 ) ( n − i ) ( m − j ) \sum_{i\leq i\leq n}\sum_{1\leq\ j\leq n}(\gcd(i, j)-1)(n-i)(m-j) ∑i≤i≤n∑1≤ j≤n(gcd(i,j)−1)(n−i)(m−j)
AC代码
#include BZOJ 4403. 序列统计
题目链接
题面
统计长度在 1 ∼ N 1\sim N 1∼N之间, 元素大小都在 L L L到 R R R之间的单调不下降序列的数量
解析
将 L ∼ R L\sim R L∼R之间的数映射到 0 ∼ R − L 0\sim R-L 0∼R−L区间,使得每个数满足条件
0 ≤ a 1 ≤ a 2 ≤ ⋯ ≤ a k ≤ R − L 0\leq a_1\leq a_2\leq\dots\leq a_k\leq R-L 0≤a1≤a2≤⋯≤ak≤R−L
不妨做如下映射
{ x 1 = a 1 x 2 = a 2 − a 1 x 3 = a 3 − a 2 ⋮ x k = a k − a k − 1 ∑ i = 1 k x i = a k ≤ R − L \left\{ \begin{aligned} &x_1=a_1\\ &x_2=a_2-a_1\\ &x_3=a_3-a_2\\ &\vdots \\ &x_k=a_k-a_{k-1} \end{aligned} \right.\\ \sum_{i=1}^k x_i=a_k\leq R-L ⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧x1=a1x2=a2−a1x3=a3−a2⋮xk=ak−ak−1i=1∑kxi=ak≤R−L
转化为找到一组 x i x_i xi使得以下不等式成立,求方案数问题
x 1 + x 2 + ⋯ + x k ≤ R − L x i ≥ 0 \begin{aligned} &x_1+x_2+\dots+x_k\leq R-L\\ &x_i\geq 0 \end{aligned} x1+x2+⋯+xk≤R−Lxi≥0
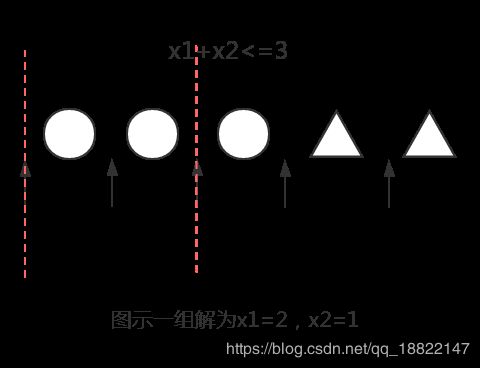
使用隔板法可以推算出方案数为 C R − L + k k C_{R-L+k}^k CR−L+kk,对 k k k在 1 ∼ N 1\sim N 1∼N之间进行枚举,令 M = R − L M=R-L M=R−L,根据递推公式 C a b = C a − 1 b + C a − 1 b − 1 C_a^b=C_{a-1}^b+C_{a-1}^{b-1} Cab=Ca−1b+Ca−1b−1进行化简
∑ k = 1 N = C R − L + k k = C M + k k = C M + k M = C M + 1 M + C M + 2 M + ⋯ + C M + N M = ( C M + 1 M + 1 + C M + 1 M ) + C M + 2 M + ⋯ + C M + N M − 1 = ( C M + 2 M + 1 + C M + 2 M ) + ⋯ + C M + N M − 1 = C M + N + 1 M + 1 − 1 = C R + L + N + 1 R − L + 1 − 1 \begin{aligned} \sum_{k=1}^N&=C_{R-L+k}^k=C_{M+k}^k=C_{M+k}^M \\ &=C_{M+1}^M+C_{M+2}^M+\dots+C_{M+N}^M \\ &=(C_{M+1}^{M+1}+C_{M+1}^M)+C_{M+2}^M+\dots+C_{M+N}^M-1\\ &=(C_{M+2}^{M+1}+C_{M+2}^M)+\dots+C_{M+N}^M-1\\ &=C_{M+N+1}^{M+1}-1\\ &=C_{R+L+N+1}^{R-L+1}-1 \end{aligned} k=1∑N=CR−L+kk=CM+kk=CM+kM=CM+1M+CM+2M+⋯+CM+NM=(CM+1M+1+CM+1M)+CM+2M+⋯+CM+NM−1=(CM+2M+1+CM+2M)+⋯+CM+NM−1=CM+N+1M+1−1=CR+L+N+1R−L+1−1
组合数算法使用Lucas定理,时间复杂度为 O ( P log N P ) \mathcal{O}(P\log_N^P) O(PlogNP).
AC代码
#include