二部图（二分图）总结
1 二部图
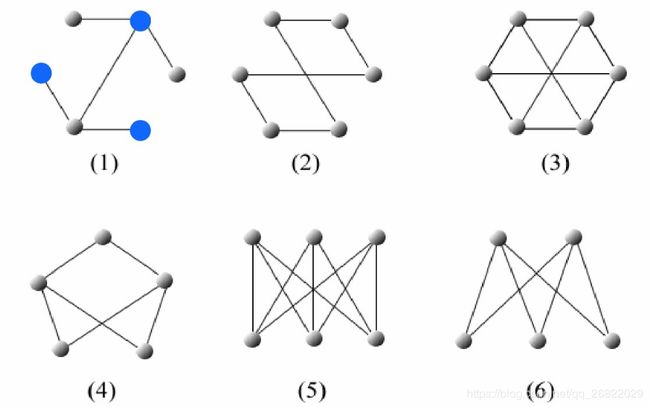
二部图又叫二分图，是图论中的一种特殊模型。设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交子集 ，使得每一条边都分别连接两个集合中的顶点。如果存在这样的划分，则此图为一个二分图，如下图所示的六个图全都是二分图：
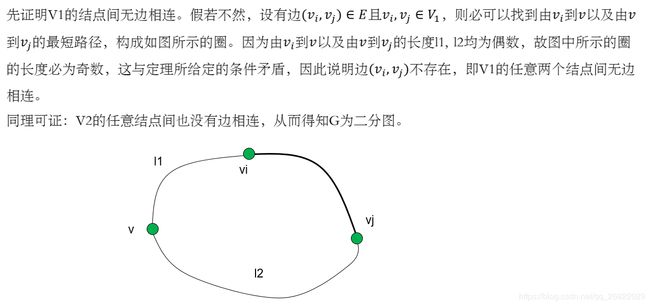
关于二部图有一个重要的定理：G为二部图的充要条件是G中的每一个圈的长度都是偶数。证明过程如下：
2 匹配问题
设G=
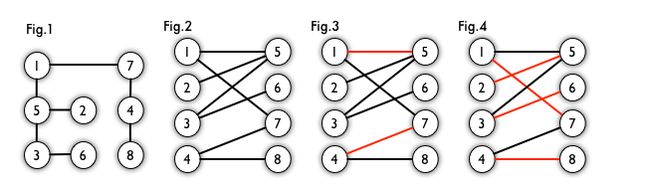
最大匹配：图 4 是一个最大匹配，它包含 4 条匹配边。
完美匹配：图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。
关于匹配问题还有以下四个重要的定义：
设M是一个匹配，则：
- V1中的结点u和V2中的结点v称被M所匹配，当且仅当有杆e属于M，使得e=（u, v）
- 结点u被称为M的饱和点当且仅当有杆e属于M匹配结点u；否则结点u称为M的非饱和点
- 交错路P是一条分别交替的属于M和E\M的边构成的极大的初级路（或圈）；
- 增广路P是一条起点为u以及终点为v且都是非饱和点的交错路。
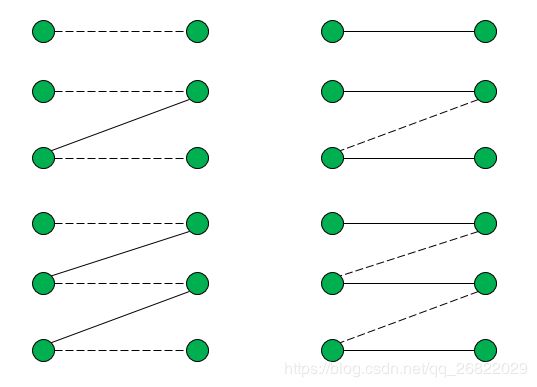
下图中左边的路都是交错路，也是增广路，其端点都是非饱和点，实线所表示的边都是匹配中的边。如果我们像右边的图那样，将左边路中的实线变成虚线边，将虚线边变成实线边就可以逐步增加匹配中的边，从而使得匹配达到最大匹配。接下来介绍的求最大匹配的算法就是基于这种思想。
3 匈牙利算法
匈牙利算法思想：通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（增广路定理）。
匈牙利算法计算步骤：
No 1任取一匹配M (可以是空集或者只含有一条边的集合）；
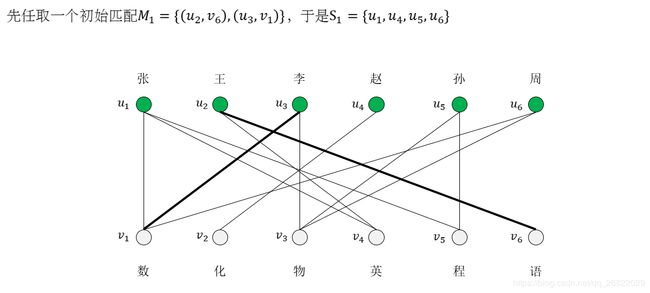
No 2令S = {u|u∈V1∩u是M的非饱和点}，若S为空集，则M已经是最大匹配，exit;
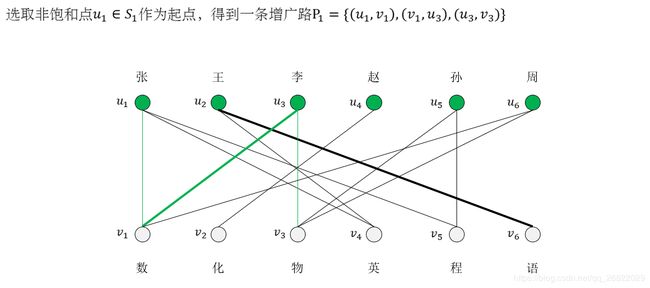
No 3否则，S不为空，任取一非饱和点u0作为起点，从此起点走出几条交错路 Pil， Pi2,…；
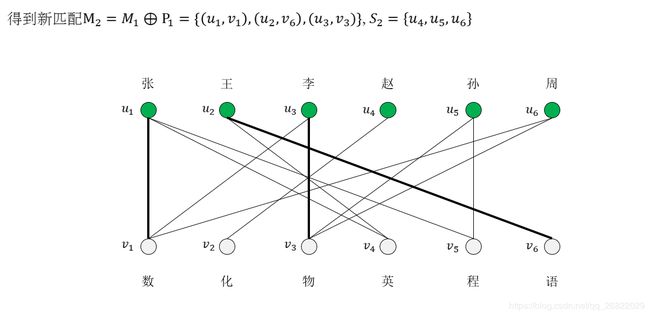
No 4如果它们中有某条路P是增广路（即P的终点也是非饱和点），则令M(M\P)U(P\M)(并且满足|M| (新)=|M| (旧)+1)，回到No 3;
No 5否则，如果它们中无一条是增广路（即终点全是饱和点），则令S=S\{u0}。如果S不为空，则回到No3; 否则S为空，则M就是最大匹配，exit
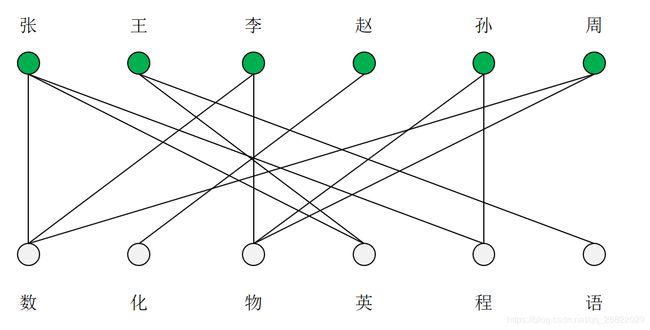
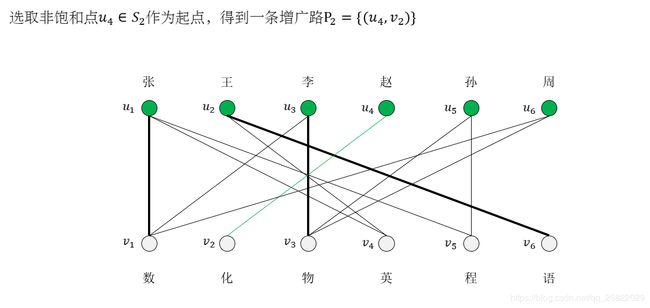
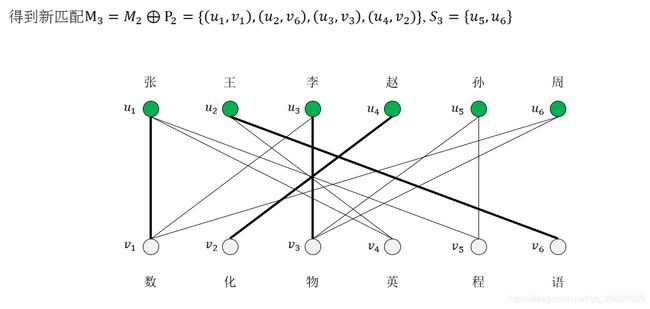
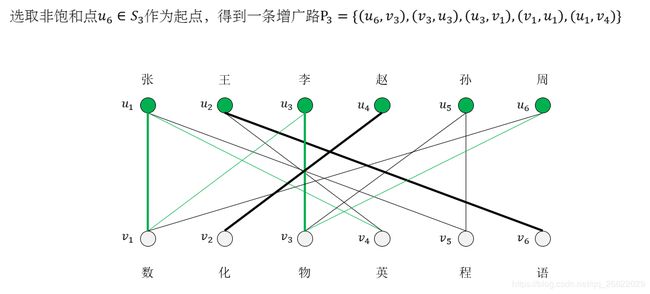
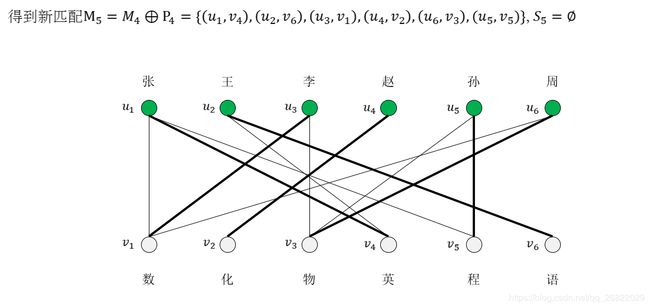
[例子]有六位教师：张、王、李、赵、孙、周，要安排他们去教六门课程：数学、化学、物理、语文、英语和程序设计。张老师会教数学、程序设计和英语；王老师会教英语和语文；李老师会教数学和物理；赵老师会教化学；孙老师会教物理和程序设计；周老师会教数学和物理。应该怎么样安排课程才能使每门课都有人教，每个人都只教一门课而且不至于使任何人去教他不懂的课？
这是一个工作分派问题，并且是图论中求二分图的完美匹配的典型问题：六个老师、六门课程的匹配。可以将教师和课程分别看做二分图中的两个互补的节点子集，当某教师会教某课程时就在相应的两个节点之间连接一条边，这样按照题目要求可以画出如下图。
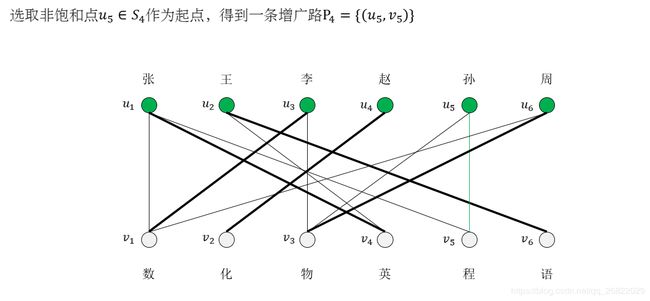
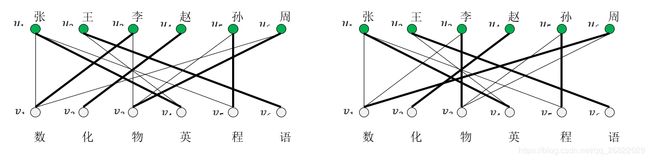
当S集合为空时，则匈牙利算法结束，得到最后的解。在二分图中，最大匹配和完美匹配并不唯一，例如上面的问题还存在这样一种完美匹配：
4 KM算法
二分图如果是没有权值的，求最大匹配，可以使用用匈牙利算法求最大匹配。如果带了权值，求最大或者最小权匹配（最佳匹配），则必须用KM算法。其实最大和最小权匹配都是一样的问题。只要会求最大匹配，如果要求最小权匹配，则将权值取相反数，再把结果取相反数，那么最小权匹配就求出来了。
KM算法 Kuhn-Munkras算法用来解决带权二分图最优匹配问题。基本思想是通过引入顶标，将最优权值匹配转化为最大匹配问题。
KM算法流程：
（1）初始化可行顶标的值；
（2）用匈牙利算法寻找完备匹配；
（3）若未找到完备匹配则修改可行顶标的值；
（4）重复（2）（3）直到找到相等子图的完备匹配为止。
[例子]婚姻匹配问题时一个经典的带权二分图问题，现在有N男N女，有些男生和女生之间互相有好感，我们将其好感程度定义为好感度，我们希望将他们两两配对，并且最后希望好感度和最大。如何选择最优的配对方法呢？可以使用KM算法求解。
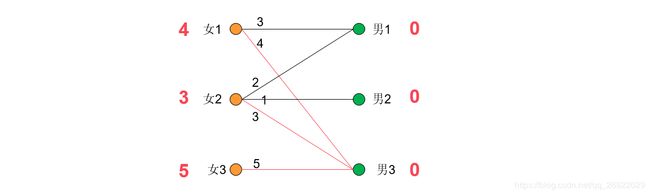
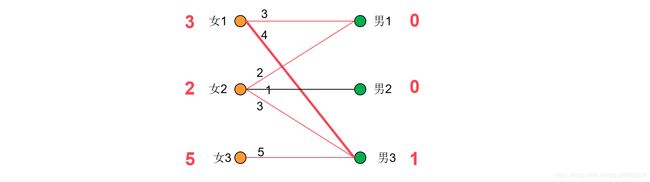
首先，每个女生会有一个期望值，就是与她有好感度的男生中最大的好感度，男生的期望值为0.
接下来开始配对，从第一个女生开始，为她找对象：因为女1+男3=4+0=4，满足“男女两人的期望等于两人之间的好感度”规则。
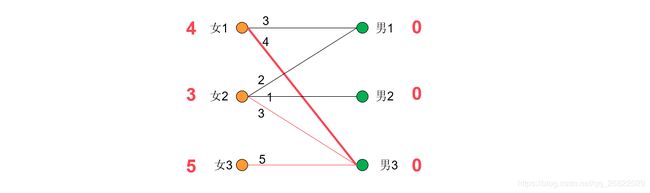
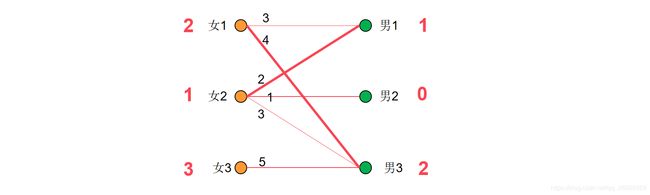
给女2找对象，因为：女2+男3=3+0=3，满足要求，但是男3已经有对象了，因此给女2找对象失败。接下来需要修改期望值：将发生冲突的女1和女2的期望值降低1，而将冲突源男3的期望值增加1.如此一来女1和男3仍然满足匹配，与男1也满足匹配。女2与男1，男3均满足匹配。修改期望值之后，继续给女2找对象。此时女2-男1匹配，同时女1-男3也匹配。
接下来给女3匹配对象，因为女3+男3=6！=5，因此无法给女3找到匹配。所以让女3的权值减1，此时女3和男3匹配了，但是又和女1冲突了。便去寻找女1，但是对于女1而言可匹配的男1已经和女2 匹配了，于是再去寻找女2。
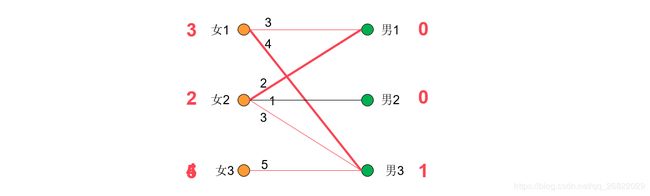而此使对于女2而言，没有其他的边满足匹配规则了，因为现在的寻找路径为：
女3->男3->女1->男1->女2，因此需要将左边的女1，2，3结点权值均减去1，将男1，3的权值均加1.
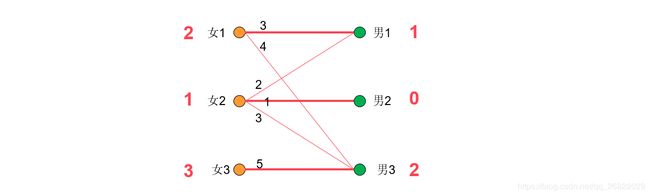
此时对于女1,2,3而言，男1,2,3均已经满足他们的期望值，也就是说现在已经将带权图转换为了无权图。因此接下来的男女匹配问题就可以使用匈牙利算法来实现，下图给出了解。
在这个问题中，冲突一共发生了三次，所以一共降低了3次效率值，但是每次降低的效率值都是最小的，所以完成的仍是最优匹配。这就是KM算法的整个过程。整体思路就是：每次都帮一个顶点匹配最大权重边，利用匈牙利算法完成最大匹配，最终完成的就是最优匹配。
5 应用
双聚类技术最早是为了满足分析基因表达数据的需要而提出的。基因是一个生命有机体向其后代传递特征的单元。典型的，基因驻留在一个DNA段中。对于所有生物，基因都是至关重要的，因为他们确定所有的蛋白质和功能RNA链。他们持有用来构建和维持生命有机体细胞和传递遗传特征到后代的信息。功能基因的合成产生RNA或者蛋白质，依赖于基因表达过程。基因型是细胞、有机体或者个体的基因组成。
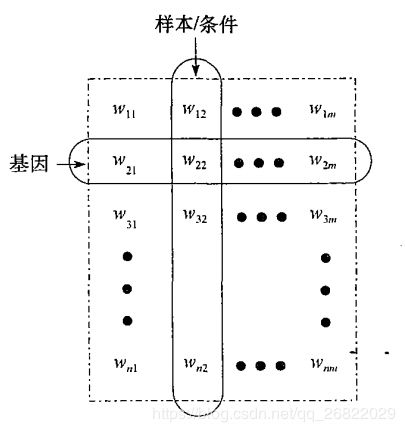
使用DNA图谱和其他生物工程技术，我们可以在大量不同的实验条件下，测量一个有机体的大量基因的表达水平。这些条件可能对应于实验中的不同时间点或者取自不同的器官的样本。粗略来说，基因表达数据或者DNA微阵列数据概念上是一个基因-样本/条件矩阵，其中每一行对应于一个基因，每一列对应于一个样本或条件。矩阵的每一个元素都是实数，记录一个基因在特定条件下的表达水平，如下图所示：
生信方向的研究表明，在人体内存在一种机制：某些基因的表达能够抑制另一部分基因的表达，因此如何将这两种基因分别找出来在临床治疗上有重要的意义。可以将这个问题抽象成为一个二部图问题，最终尽可能的将这两部分基因划分成两个集合。每一个基因即可看作是一个G中的一个点。