【NLP】图解从RNN到seq2seq+Attention
从RNN到seq2seq+Attention
前言
本篇将从 RNN 的角度出发,一步一步进阶到 seq2seq 以及加了 Attention 的 seq2seq。
宏观上看看什么是seq2seq
Seq2Seq 是一个 Encoder-Decoder 结构的神经网络,它的输入是一个序列(Sequence),输出也是一个序列(Sequence),因此而得名Seq2Seq。
- 在
Encoder中,将可变长度的序列转变为固定长度的向量表达 - 在
Decoder中,将这个固定长度的向量转换为可变长度的目标的信号序列
Seq2seq被广泛应用在机器翻译、聊天机器人甚至是图像生成文字等情境
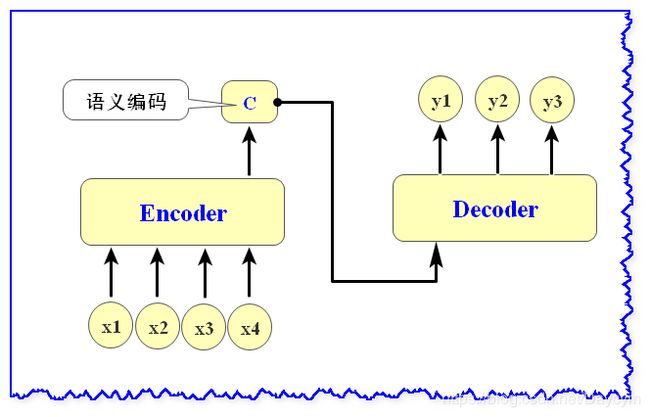
上图是 Seq2Seq 模型工作的流程,描述如下:
Seq2Seq包括输入、Encoder、中间状态向量C、Decoder、输出Encoder阶段,通过学习输入,将其编码为一个固定大小的状态向量C(也称为语义编码)Decoder阶段,通过对状态向量C的学习输出对应的序列
Seq2Seq核心就在于Encoder和Decoder,因此是一个Encoder-Decoder结构的神经网络
RNN谈起
- 对于RNN不了解的可以参考:【深度学习】从循环神经网络(RNN)到LSTM和GRU
单层网络
有点基础的,相信大家对如下结构都不陌生:
y = f ( W x + b ) y = f(Wx+b) y=f(Wx+b)
输入是 x x x,经过隐藏层 h h h 变换( W x + b Wx+b Wx+b)和激活函数 f f f 得到输出 y y y
经典的RNN结构(N vs N)
但是在现实世界,我们的输入往往不是一个x,而是一个序列,这就需要一个能够接受序列数据输入的网络。
循环神经网络(RNN)便是一类用于处理序列数据的神经网络,就像卷积神经网络是专门用于处理网格化数据(如一张图像)的神经网络,循环神经网络时专门用于处理序列 x ( 1 ) , x ( 2 ) , . . . , x ( n ) x^{(1)},x^{(2)},...,x^{(n)} x(1),x(2),...,x(n) 的神经网络。
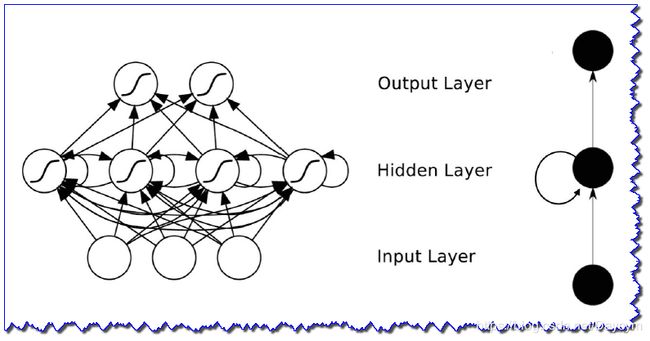
RNN 网络结构如下:
它就是单层网络的重复
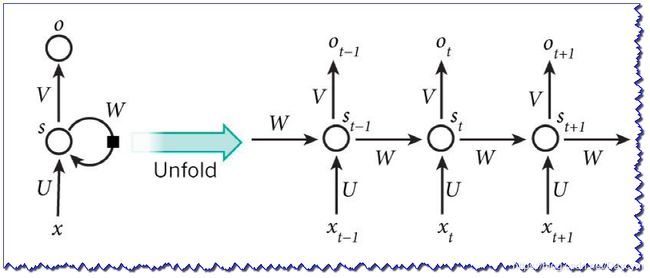
将序列按时间展开就可以得到RNN的结构,如下图:
针对不同的任务,RNN的输入不同:
- 对于自然语言处理问题,x1可以看作是第一个单词,x2可以看作是第二个单词,依次类推;
- 语音处理,此时,x1、x2、x3…便是每帧的语音信号
- 股价预测问题,x就可以是每天的股价
- …
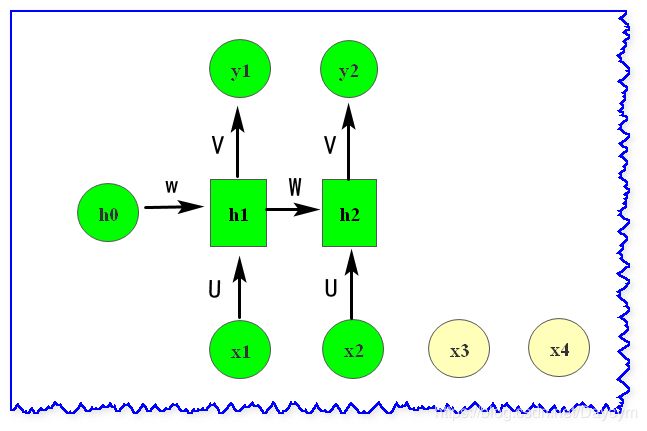
具体计算过程
h 1 = f ( U x 1 + W h 0 + b ) h1 = f(Ux_1 + Wh_0+b) h1=f(Ux1+Wh0+b)
y 1 = s o f t m a x ( V h 1 + c ) y1 = softmax(Vh_1+c) y1=softmax(Vh1+c)
h 2 = f ( U x 2 + W h 1 + b ) h2 = f(Ux_2 + Wh_1+b) h2=f(Ux2+Wh1+b)
y 2 = s o f t m a x ( V h 2 + c ) y2 = softmax(Vh_2+c) y2=softmax(Vh2+c)
进行同样地操作,就会得到如下结构(其中 U , W , V U,W,V U,W,V都是一样的,也就是参数共享):
h 3 = f ( U x 3 + W h 2 + b ) h3 = f(Ux_3 + Wh_2+b) h3=f(Ux3+Wh2+b)
y 3 = s o f t m a x ( V h 3 + c ) y3 = softmax(Vh_3+c) y3=softmax(Vh3+c)
h 4 = f ( U x 4 + W h 3 + b ) h4 = f(Ux_4 + Wh_3+b) h4=f(Ux4+Wh3+b)
y 4 = s o f t m a x ( V h 4 + c ) y4 = softmax(Vh_4+c) y4=softmax(Vh4+c)
以上就是RNN的基本结构了,是不是很简单,其实就是单层网络的叠加。上面我们只计算到 x 4 x4 x4,理论上,RNN 可以无限计算下去的,无论多长的序列,都可以按照上面的方式叠加。
不知道大家有没有发现,RNN的每一个时刻都有一个输出,也就是说,如果输入序列/时间序列长度为 N ,那么输出序列的长度也为 N。这就是典型的 N vs N
由于这个限制,经典的RNN的适用范围比较小
N vs 1
在有些情况下,我们需要输入的是一个序列,输出的是一个类别,经典的RNN就无法直接解决。事实上,我们只需要在RNN的最后一个进行输出变换即可,无需每一个h都输出一个值,结构如下:
y = s o f t m a x ( V h 4 + c ) y = softmax(Vh_4 + c) y=softmax(Vh4+c)
这种结构通常用来处理序列分类问题,例如:
- 输入一段文本判断它所属的类别
- 输入一个句子,判断它的情感倾向
- 输入一段视频,判断它的类别等等
1 vs N
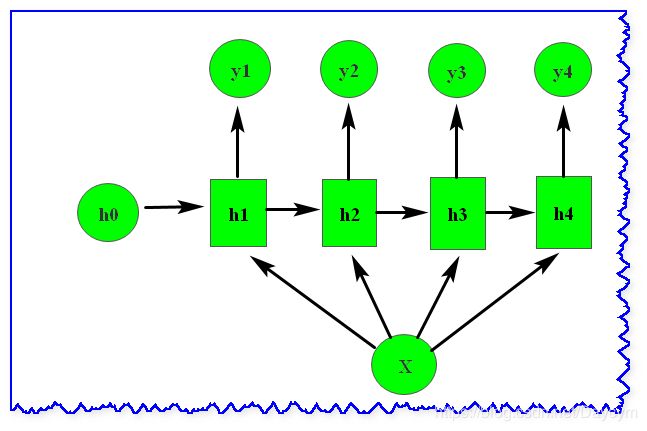
结构一(只在输入开始时输入计算):
结构二(输入信息X作为每个阶段的输入):
这种1 VS N的结构可以处理的问题有:
- 从图像生成文字,此时输入的X就是图像的特征,而输出的y序列就是一段句子;
- 从类别生成语音或音乐等
通过上面的内容,我们已经知道了如何解决 N vs N、N vs 1 和 1 vs N 的问题,细心的人会发现,有了多对多(相同长度)、多对一和一对多,那么要是多对多但是长度不一样了,又该如何解决呢?接下来,我们的重点来了
(Seq2Seq)Encoder-Decoder模型(N vs M)
原始的 N vs N 的 RNN 模型要求输入输出序列等长,然后我们遇到的大部分问题的输入和输出序列是不相等的,例如,机器翻译中,源语言和目标语言的句子往往并没有相同的长度。
而本节要介绍的 Encoder-Decoder模型 便是 RNN 最重要的变种,也可以称为 Seq2Seq模型,在本篇的开始,我们已经了解了它的整体框架。
这里我们用机器翻译任务来介绍:
Encoder-Decoder结构先将输入数据编码成一个上下文向量 C C C
图中红外块就是上下文向量 C C C
得到 C C C 有多种方式,最简单的方法就是把Encoder的最后一个隐状态赋值给 C C C ,还可以对最后的隐状态做一个变换得到 C C C,也可以对所有的隐状态做变换。
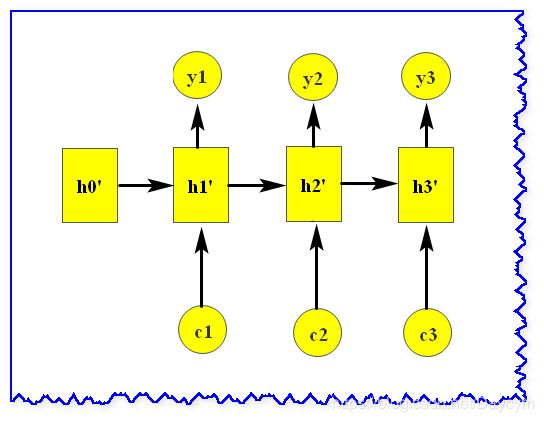
- 得到 C C C 之后,就用另一个RNN网络对其进行解码,这部分RNN网络被称为Decoder。具体做法就是将 C C C 当做之前的初始状态 h 0 h_0 h0 输入到Decoder中:
- 还有一种做法是将 C C C当做每一步的输入:
由于这种Encoder-Decoder结构不限制输入和输出的序列长度,因此应用的范围非常广泛,比如:
- 机器翻译:
Encoder-Decoder的最经典应用,事实上这一结构就是在机器翻译领域最先提出的; - 文本摘要: 输入是一段文本序列,输出是这段文本序列的摘要序列;
- 阅读理解: 将输入的文章和问题分别编码,再对其进行解码得到问题的答案;
- 语音识别: 输入是语音信号序列,输出是文字序列。
Attention机制
但是,在Seq2seq模型中,Encoder 将输入句压缩成固定长度的 context vector 真的好吗?如机器翻译问题,当要翻译的句子较长时,固定长度的 context vector就很容易忘记前面的内容,导致效果不好。那么该怎么办呢?
这时候,Attention 就派上用场了(这词看上去高大上,其实本质上就是加权问题,只是给了一个高大上的名字)
Attention 机制通过在每个时间输入不同的 c c c 来解决这个问题,输入的 c c c 由 Decoder 自己决定。下图是带有 Attention 机制的 Decoder:
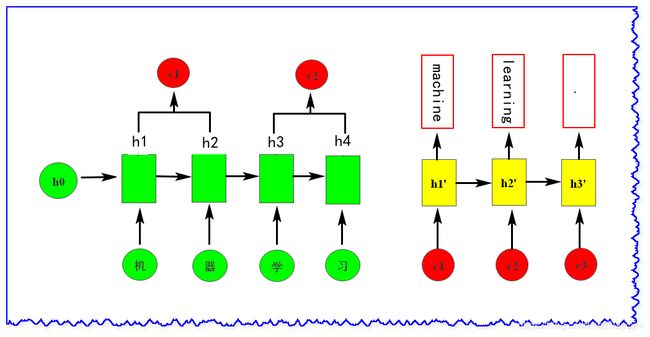
以机器翻译为例,如图:
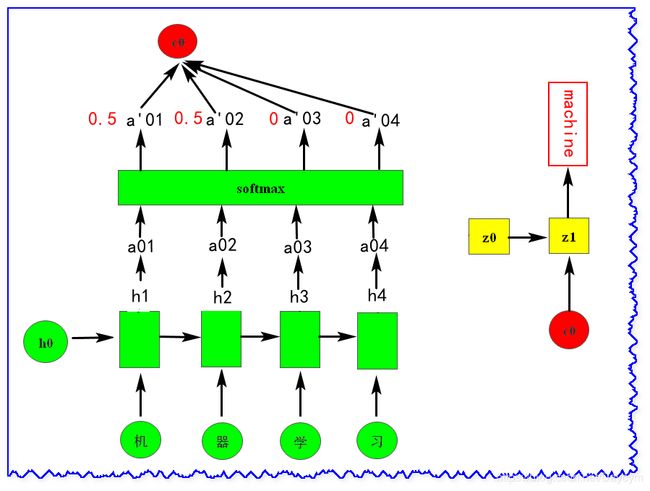
我们在进行 Encoder 时,会保存下每个 h h h (这里的 h h h 不用是RNN的输出,当然也可以是RNN的输出,但是如果输出的维度较大,而且输出仅仅是 h h h 通过转换得到,存输出可能需要更多的空间来存储,那还不如直接存 h h h );在进行 Decoder 时,就像在做搜寻一样,在生成第一个词machine的时候,就去搜寻它要的东西,在它看了 h h h 之后,假设从 h 1 , h 2 h_1,h_2 h1,h2 中抽取出 c 1 c_1 c1(后面介绍 c 1 c_1 c1 是怎么抽取出来的),然后作为Decoder的第一个输入;生成第二个词的时候,它会再一次看一下 h h h,又从 h 3 , h 4 h_3,h_4 h3,h4中抽取出 c 2 c_2 c2;同样又抽取出 c 3 c_3 c3(图中未画出)。
在原本的Seq2Seq模型中,
Decoder每次的输入都是一样的,而加了Attention机制后,每次输入都是由Decoder自行搜索得到的
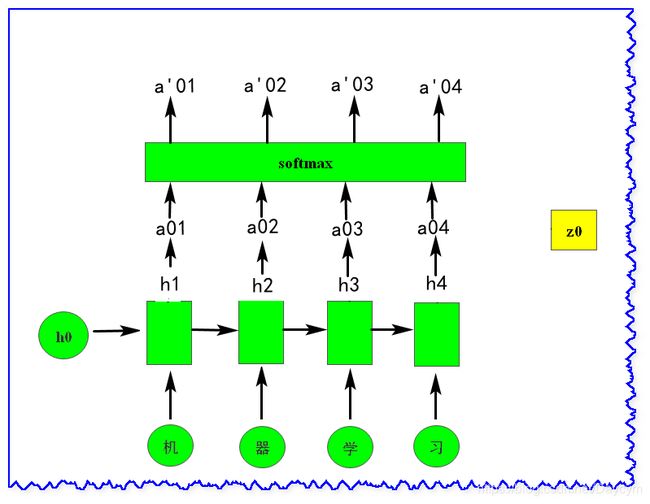
那么c是如何得到呢?
上图中的 z 0 z0 z0 我们可以看作是一个关键字,用这个关键字去和每一个 h h h 进行匹配得到一个 a a a 值,而这里的 z 0 z0 z0 其实也是神经网络的参数,
match方法也可以由自己自行设计来比较 z z z 和 h h h 的相似(匹配)程度。
上图对得到的每个 a a a 又做了次
softmax,是所有值的和为1,这一步可以做也可以不做,有时候好,有时候不好,看你高兴吧。
c 0 = ∑ a 0 i h i c^0 = \sum a_0^ih^i c0=∑a0ihi
= 0.5 h 1 + 0.5 h 2 = 0.5h^1+0.5h^2 =0.5h1+0.5h2
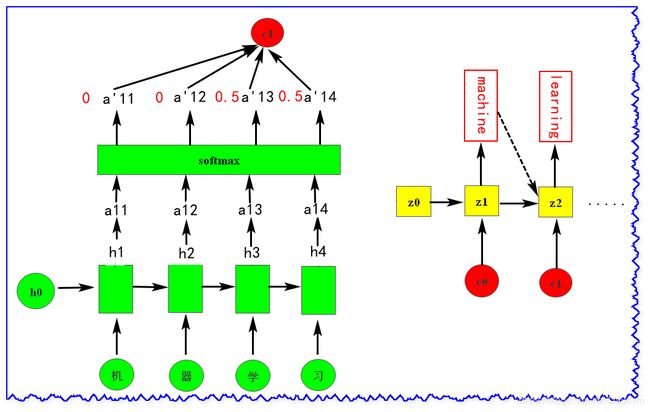
c 1 = ∑ a 1 i h i c^1 = \sum a_1^ih^i c1=∑a1ihi
= 0.5 h 3 + 0.5 h 4 = 0.5h^3+0.5h^4 =0.5h3+0.5h4
按照上面同样地操作,直到遇到句号或
上面我们只是简单介绍了 Attention机制,下面我们具体介绍下:
既然我们已经有了前馈神经网络和循环神经网络,而且都有较强的能力,那么为什么还需要引入 Attention机制,前面我们提到一个重要问题就是计算问题。
- 如果我们的模型需要记住更多的“信息”,模型就会变得复杂,需要的计算量也会增加,然而目前的计算能力依然限制了神经网络的发展,何况RNN无法并行计算,虽然也有很多研究人员尝试使用
CNN来代替RNN,CNN实际上是透过大量的layer去解决局部信息的问题 - 虽然局部连接、权重共享以及pooling等优化操作可以让神经网络变得简单一些,有效缓解模型复杂度和表达能力之间的矛盾;但是,如循环神经网络中的长距离以来问题,信息“记忆”能力并不高
可以借助人脑处理信息过载的方式,只关注想要关心的信息。当用神经网络来处理大量的输入信息时,也可以借鉴人脑的注意力机制,只选择一些关键的信息输入进行处理,来提高神经网络的效率
前面我们提到,Attention 机制的实质其实就是一个搜索的过程,这样一来,就无须将所有的N个输入信息都输入到神经网络进行计算,只需要从X中选择一些和任务相关的信息输入给神经网络:这实际上就是Attention机制缓解神经网络复杂度的体现
Attention 机制一般计算过程可以分为如下三步:
- 信息输入: X = [ x 1 , x 2 , . . . , x N ] X = [x_1, x_2, ... ,x_N] X=[x1,x2,...,xN]表示N个输入
- 计算注意力分布 α \alpha α(等同于前面的 a a a)
α i ^ = s o f t m a x ( s ( x i , q ) ) \hat{\alpha_i}=softmax(s(x_i,q)) αi^=softmax(s(xi,q))
这里s函数为注意力打分机制,例如:
- 加性模型: s ( x i , q ) = V T t a n h ( W x i + U q ) s(x_i,q)=V^Ttanh(Wx_i+Uq) s(xi,q)=VTtanh(Wxi+Uq)
- 点积模型: s ( x i , q ) = X i T q s(x_i,q)=X_i^Tq s(xi,q)=XiTq
- 缩放点积模型: s ( x i , q ) = X i T q d s(x_i,q)=\frac{X_i^Tq}{\sqrt{d}} s(xi,q)=dXiTq
- 双线性模型: s ( x i , q ) = X i T W q s(x_i,q)=X_i^TWq s(xi,q)=XiTWq
- 根据 α \alpha α来计算输入信息的加权和/加权平均
a t t ( q , X ) = ∑ i = 1 N α i ^ X i att(q,X) = \sum_{i=1}^N\hat{\alpha_i}X_i att(q,X)=i=1∑Nαi^Xi
截至目前为止,我们介绍的 Attention 机制只是最普通的,是软性注意力(其选择的信息是所有输入信息在注意力分布下的期望),它还有一些变种:
- 硬性注意力:只关注到某一个位置上的信息,硬性注意力有两种实现方式:
- (1)一种是选取最高概率的输入信息;
- (2)另一种硬性注意力可以通过在注意力分布式上随机采样的方式实现。
硬性注意力模型的缺点:硬性注意力的一个缺点是基于最大采样或随机采样的方式来选择信息。因此最终的损失函数与注意力分布之间的函数关系不可导,因此无法使用在反向传播算法进行训练。为了使用反向传播算法,一般使用软性注意力来代替硬性注意力。硬性注意力需要通过强化学习来进行训练。
- 多头注意力:
multi-head attention是利用多个查询 Q = [ q 1 , . . . , q M ] Q = [q_1,...,q_M] Q=[q1,...,qM],来平行地计算从输入信息中选取多个信息。每个注意力关注输入信息的不同部分,然后再进行拼接。
多头注意力在transformer中有应用
总结
通过上面的内容,我们介绍了 Seq2Seq 和 Seq2Seq+Attention的运作和计算方式,是不是很简单?虽然 Seq2Seq 解决了 RNN 输入输出序列长度一样的问题,但是由于其 Encoder-Decoder 部分的神经网络还是使用的 RNN 或其变种,因此 RNN 存在的问题:无法平行化处理,导致模型训练的时间很长, Seq2Seq 依然存在。
庆幸的是,在2017年,Google 提出了一种叫做 The transformer 的模型,透过 self attention、multi-head 的概念去解决上述缺点,完全舍弃了RNN、CNN的构架。我们将在下篇博客中来详细介绍。
本篇为博主初入学习笔记,日后会不断提炼里面的一些说法,如若读者有更好的表达,还望指出,不胜感激!!!