数学建模之方差分析基础--单因素，双因素方差分析与matlab实现

前言

由于方差分析的原理基本在所有概率论与数理统计的书中都可以找到，那么这里就直接以图片的形式呈现了。关于方差齐次性检验以后会补充。知识基础：假设检验。（今天刚刚学了数据结构，发现自己以前写的数组的基础操作水平极低，真是惭愧）

简介

方差分析(Analysis of Variance，简称ANOVA)，又称“变异数分析”，是R.A.Fisher发明的，用于两个及两个以上样本均数差别的显著性检验。 由于各种因素的影响，研究所得的数据呈现波动状。造成波动的原因可分成两类，一是不可控的随机因素，另一是研究中施加的对结果形成影响的可控因素。（百度百科）简单来说就是看看不同因素对于样本的总体均值影响。

原理

• 单因素实验的方差分析：

（里面有一个地方写错了，应该是F分布的α分位点， 而不是（1-α）分位点。因为如果原假设不成立，那么组间的影响就会比较大，也就是SA比较大，对应F也就较大，而α对应的是落入拒绝域的概率，即P(F>threshold）=α，即threshold等于F的α分位点）

• 双因素的方差分析
  
  
  
  
  
  （同样的，这里的分位点应该是α）

代码实现

• 注意事项
  从原理中我们可以看到方差分析的假设是各因素水平对应的样本要服从同方差的正态分布，因此我们有必要做正态拟合度检验和方差齐次检验！（数据量比较大的时候采用，数据量少的时候没有必要）

%初始化数据：这里我们设置的数据是单因素5个水平下的五组标准
%正态分布的数据，以确保数据能通过检验
for i=1:5
    x(i,:)=randn(1,5);
end
%正态性检验（卡方检验）
for i=1:5
    [h,p]=lillietest(x(i,:));
    judge(i)=p;%这里算出来的p是χ^2对应的p分位点，因此当p>0.05时，χ^2落入
               %接受域，原假设成立，可以看作正态分布
end
judge
%方差齐次检验
X=reshape(x',size(x,1)*size(x,2),1);%注意形式，将x按行展开
%数据对应的因素水平序号
ind=[ones(1,5),2*ones(1,5),3*ones(1,5),4*ones(1,5),5*ones(1,5)];
[p,status]=vartestn(X,ind);%p为显著性水平，大于0.05即接受原假设：认为因素水平的影响不大
%方差齐次检验这里我不是很熟，这里简单简单应用一下，日后会补上这方面的内容

我们看一下这段代码的运行结果：

judge=0.5000    0.0741    0.2905    0.0553    0.5000

均大于0.05，满足正态分布的要求（毕竟用的就是正态分布的数据）

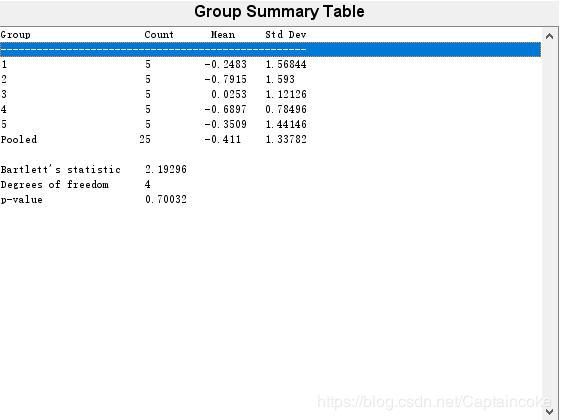
p=0.70032>0.05，满足方差齐次检验的要求

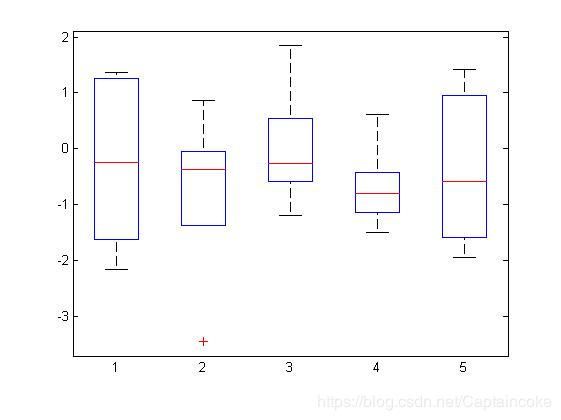
箱线图：从上至下分别为：最大值，上四分位数，中位数，下四分位数，最小值。红色的点是离群异常点。

• 单因素

[p,table,status]=anova1(X,ind)
%p:为显著性水平，同样>0.05即可
%table：方差分析表
%status：后面的多重分析会用到

结果：
p =

0.3350

table =

'Source'    'SS'         'df'    'MS'        'F'         'Prob>F'
'Groups'    [ 5.4734]    [ 4]    [1.3683]    [1.2166]    [0.3350]
'Error'     [22.4947]    [20]    [1.1247]          []          []
'Total'     [27.9681]    [24]          []          []          []

info =

gnames: {5x1 cell}
     n: [5 5 5 5 5]
source: 'anova1'
 means: [0.4099 0.0779 -0.7779 -0.0130 0.5745]
    df: 20
     s: 1.0605

其中p>0.05，则接受原假设，认为因素无显著影响，反之认为因素有影响
table则对应着方差分析表（具体数字的解读参见原理）


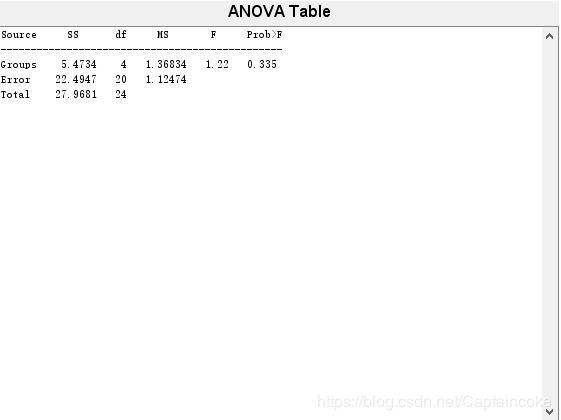
这个箱线图含义与之前的相似，添加的部分是均值的置信区间（由中位数开始指出去的那4条斜线形成的梯形较长底边所在的位置，如第一个的置信区间就约为[-1,1.6]

[c m h gnames]=multcompare(status);
%c：比较矩阵，m：每组的均值的估计值和相应的标准差
%h:图形句柄 gnames：水平等级
head={'组序号','组序号','置信下限','组均值差','置信上限','?'};%最后一列意义不明
[ head ;num2cell(c)]%c:比较结果矩阵
[gnames num2cell(m)]%每组的均值的估计值和相应的标准差

更多关于multcompare的参数和返回值可参见大神文章：MATLAB方差分析
结果：
ans =

'组序号'    '组序号'    '置信下限'       '组均值差'       '置信上限'      '?'     
[  1]    [  2]    [-1.1323]    [ 0.8093]    [2.7509]    [0.7247]
[  1]    [  3]    [-1.7358]    [ 0.2058]    [2.1474]    [0.9976]
[  1]    [  4]    [-1.5378]    [ 0.4038]    [2.3454]    [0.9697]
[  1]    [  5]    [-1.5169]    [ 0.4247]    [2.3663]    [0.9637]
[  2]    [  3]    [-2.5451]    [-0.6035]    [1.3381]    [0.8818]
[  2]    [  4]    [-2.3471]    [-0.4055]    [1.5361]    [0.9693]
[  2]    [  5]    [-2.3262]    [-0.3846]    [1.5570]    [0.9746]
[  3]    [  4]    [-1.7436]    [ 0.1980]    [2.1396]    [0.9979]
[  3]    [  5]    [-1.7227]    [ 0.2189]    [2.1605]    [0.9970]
[  4]    [  5]    [-1.9206]    [ 0.0210]    [1.9626]    [1.0000]

ans =

'1'    [ 0.6907]    [0.4588]
'2'    [-0.1186]    [0.4588]
'3'    [ 0.4850]    [0.4588]
'4'    [ 0.2870]    [0.4588]
'5'    [ 0.2660]    [0.4588]

multcompare函数还生成一个交互式图形，可以通过鼠标单击的方式进行两两比较检验。该交互式图形上用一个符号（圆圈）标出了每一组的组均值，用一条之间段标出了每个组的组均值的置信区间。如果某两条线段不相交，即没有重叠的部分，则说明这两个组的组均值之间的差异是显著的。如果某两条直线段有重叠部分，则说明这两个组的组均值之间的差异是不显著的。可以用鼠标在图上任意选一个组，选中的组以及与选中的组禅意显著的其他组均用高亮显示，选中的组用蓝色显示，与选中的组差异显著的其他组用红色显示。
————————————————
版权声明：本文为CSDN博主「MATLAB讲师」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文传送门：https://blog.csdn.net/matlab_matlab/article/details/57076854
图（交互式）中任何均值都在其他均值的置信区间内，可见均值的差别并不大

• 多因素
  操作与单因素类似，只不过要注意输入数据矩阵的形式，每一个Xijk(k=1~t)在矩阵中对应的位置如下：

 	B1		B2.....	Bi.....Bn
 A1	X111	X121.............
 	X112	X122.............
 	...	    ...	.............
 	X11t	X12t.............
 A2 X211	X221.............
 	X212	X222.............
 	...		...	.............
 	X21t	X22t..............
 ...
 Aj					Xij1
 					Xij2
 					...
 					Xijt
 ...
 An

clc,clear 
x0=[58.2,52.6 56.2,41.2 65.3,60.8 
49.1,42.8 54.1,50.5 51.6,48.4 
60.1,58.3 70.9,73.2 39.2,40.7 
75.8,71.5 58.2,51.0 48.7,41.4]; 
x1=x0(:,1:2:5);x2=x0(:,2:2:6); 
for i=1:4 
 x(2*i-1,:)=x1(i,:); 
 x(2*i,:)=x2(i,:); 
end
[p,t,st]=anova2(x,2)
%anvoa2(x,t) 这里的t就是一组因素水平作用下样本的样本数量

结果：
p =

0.0035    0.0260    0.0001

t =

'Source'         'SS'            'df'    'MS'          'F'          'Prob>F'    
'Columns'        [  370.9808]    [ 2]    [185.4904]    [ 9.3939]    [    0.0035]
'Rows'           [  261.6750]    [ 3]    [ 87.2250]    [ 4.4174]    [    0.0260]
'Interaction'    [1.7687e+03]    [ 6]    [294.7821]    [14.9288]    [6.1511e-05]
'Error'          [  236.9500]    [12]    [ 19.7458]           []              []
'Total'          [2.6383e+03]    [23]            []           []              []

st =

  source: 'anova2'
 sigmasq: 19.7458
colmeans: [58.5500 56.9125 49.5125]
    coln: 8
rowmeans: [55.7167 49.4167 57.0667 57.7667]
    rown: 6
   inter: 1
    pval: 6.1511e-05
      df: 12

这里p均<0.05，则拒绝原假设，认为在不同A，B水平下均值的差异还是很大的，而且AB的交互作用也是很显著的。

%多元分析
[c_A,m_A,h_A,ganmes_A]=multcompare(st,'estimate','row')%行：对因素A进行多重分析
[c_B,m_B,h_B,ganmes_B]=multcompare(st,'estimate','column')%列：对因素B进行多重分析

结果解读与对应单因素多重分析的结果一致
PS：有不正确或者不详细的地方欢迎在留言区提出，大家一起学习