显著目标检测论文(三)——Minimum Barrier Salient Object Detection at 80 FPS (2015)

这篇文章最大的亮点就是其实时性, 80 fps. 个人感觉论文的效果还是很惊艳的. 可以先看看论文的效果. 如 Figure 1 所示.

作者使用的机器配置如下:

• 3.2GHz x 2 CPU
• 12G RAM

论文中提出了 MB 方法和 MB+ 方法. 其中 MB 的代码使用 C 实现, MB+ 的代码使用 matlab 实现. 这里的 80 fps 指的是 MB 的运行速度.

另外, 没有计算 I/O 的时间消耗, 没有使用并行计算来同时处理多张图片.

源码在项目主页中给出: http://cs-people.bu.edu/jmzhang/fastmbd.html

如果项目主页失效, 可以在 github 上获取: https://github.com/jimmie33/MBS

论文中在最后给出了 3 种后处理的方法(比如 CenterMap, 形态学平滑, 对比度加强), 在几乎没有增加算法复杂度的前提下提高了 saliency-map 的效果.

论文的核心算法是基于最小化栅格距离 (MBD) 变换提出. 这个算法对像素值波动的鲁棒性很好, 因此可以直接用在 raw 像素值上, 而不必经过区域抽象化预处理(region abstraction, 处理之后可得到超像素). 但是, 由于 MBD 算法的复杂度很高且计算耗时, 本文提出一种 “近似 MBD” 转换的FastMBD 算法, 同时提供了误差边界分析.

在开始之前需要说明的是, 本论文基于已有的研究成果提出新的方法, 因此论文中对于已有的研究成果几乎是直接拿来就用, 并没有做太多的解释说明. 在论文阅读过程中应注意以下几点:

• 距离变换问题就是计算最小化路径问题, 距离变换得到的结果就是显著性图;
• Minimum Barrier Distance 是一个路径代价函数[8];
• FastMBD 是使用一种迭代的方法得到近似的 MBD 值;

---

1. 前言

---

显著性检测的常用假设: Image Boundary Connectivity Cue, 假设图像的边界区域往往和背景区域的相似度很高.

已有的 [geodesic-distance-based][2-3] 方法和 [diffusion-based][4-5] 方法依赖于区域抽象(region abstraction)来提取超像素. 超像素表示方法可以移除那些图像中无关的细节, 降低模型的计算复杂度. 尽管如此, 区域抽象方法依然由于其庞大的计算量而成为应用瓶颈.

本文使用"近似 [MBD][6-7]" 来测量像素和图像边界的连通性, 规避了区域抽象方法, 大幅提高了最终显著性图的计算速度. 和 geodesic-distance 相比, MBD 算法对 raw 像素波动的鲁棒性很好. 另外, 由于 geodesic-distance 变换的小权值累计现象(small-weight-accumulation), 当其应用在 raw 像素上时经常产生特别模糊的中心区域.

原始的 MBD 算法计算复杂度也很高, 本文提出一种 Fast MBD, 也称为近似 MBD. 基于快速栅格扫描算法(fast raster-scan) 算法实现, 速度是原始 MBD 的100x.

总结一下:

• 提出 Fast MBD, 提速 100x;
• 基于 Fast MBD 提出 Fast 显著目标检测算法;

---

2. Fast MBD - Fast 近似 MBD

---

Fast MBD 算法是基于 faster raster-scan 算法提出的. 另外还提供了 error bound 分析, 可用于显著目标检测, 图像/视频分割和目标候选等应用中.

---

2.1 Background: Distance Transform - 距离变换

---

图像的距离变换(Distance Transform) 是计算图像中各个像素和背景种子像素集合的距离图.

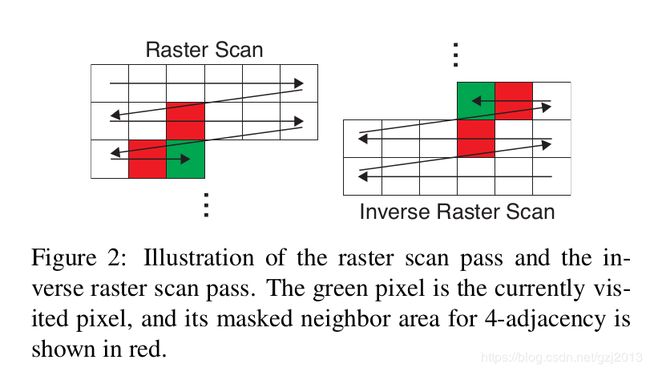
对于一张 2-D 的单通道图像, 一条路径(path) $\pi =\{\pi (0),\pi (1),\cdots ,\pi (k)\}$ 是图像 $I$ 上的一系列相邻的像素点对(例如 Figure 2 中的红绿点对). 本论文中考虑 4 条相邻的路径(即四个边界. 另外注意区分这两个"相邻"的不同).

注意, 在论文中用两个像素点组成的点对表示路径.

给定一个路径代价函数(path cost function) $F$ 和背景种子像素集合 $S$, 图像距离变换就是计算图像中各个像素和背景种子像素集合的距离图, 即对于每个像素点 t 有:

$$D(t)=\underset{\pi \in {\prod }_{S,t}}{\min }F(\pi )\text{\hspace{1em}(1)}$$

常用的路径代价函数有两种: Geodesic Distance 和 Minimum Barrier Distance.

(1) Geodesic Distance 路径代价函数

$${\sum }_I(\pi )=\sum _{i=1}^k|I(\pi (i-1))-I(\pi (i))|\text{\hspace{1em}(2)}$$

(2) Minimum Barrier Distance 路径代价函数

$${\beta }_I(\pi )=\underset{i=0}{\overset{k}{\max }}I(\pi (i))-\underset{i=0}{\overset{k}{\min }}I(\pi (i))\text{\hspace{1em}(3)}$$

其中,

• $I(\cdot )$ 表示某一点的像素值;

在种子背景图像分割中, Minimum Barrier Distance 比 geodesic distance 对噪声和模糊具有更好的鲁棒性. 但是实际的 Minimum Barrier Distance 算法的计算复杂度为 $O(mnlogn)$, n 为图像中的所有像素的数目, m 为图像中区分度比较大的像素个数. 实际中, 对于一张 200*300 的图像, 计算 MBD 需要 30s 的时间.

---

2.2 Fast MBD Transform by Raster Scan

---

参考 Fast Geodesic Distance 算法中光栅扫描 (Raster Scan) 的加速思路, 作者提出了 Fast MBD, 其本质是 MBD 变换的一种近似迭代算法.

那什么是光栅扫描?

光栅扫描(Raster Scan)是指从左往右，由上往下，先扫描完一行，再移至下一行起始位置继续扫描，H.264 编码使用的就是光栅扫描顺序。

Raster Scan 算法的扫描方向如 Figure 2 所示. 图中只给出了从左到右 (从右往左) 的扫描方向, 实际 Raster Scan 也包含从上到下(和从下到上)的扫描方向.

红色区域就是前文提到的 4 个相邻的像素, 它们和中心的绿色像素点构成 4 条不同方向的路径(path).

在使用 Raster Scan 最小化 $x$ 像素点处的路径代价函数 ${\beta }_I(\pi )$ 时, 只使用了每个像素点 $x$ 邻域的一半, 即上邻域像素点和左邻域像素点. 路径最小化操作表示如下:

$$D(x)=\text{min}\{\begin{array}{l}D(x)\\ {\beta }_I(P(y)\cdot <y,x>)\end{array}\text{\hspace{1em}(4)}$$

其中,

• $P(y)$ 是当前分配给 $y$ 像素点的路径;
• $<y,x>$ 表示从 $y$ 到 $x$ 的边缘;
• $P(y)\cdot <y,x>$ 表示 $x$ 像素点的路径, 方向为从 $y$ 到 $x$.

让 $P_y(x)=P(y)\cdot <y,x>$, 则有:

$$\beta (P_y(x))=\text{max}\{U(y),I(x)\}-\text{min}\{L(y),I(x)\}\text{\hspace{1em}(5)}$$

其中,

• $U(y),L(y)$ 分别是在路径 $P(y)$ 上的最大像素值和最小像素值;

直观的理解一下代价函数:

这个代价函数是计算显著性图的关键. 其实质还是计算像素颜色的距离.

考虑两种极端情况: 如果像素点 $x$ 出现在显著性目标所在区域的中心位置, 那么其像素值应该接近每条路径上的最大像素值; 代价函数在此处的值也就相对较大. 反之, 如果像素点 $x$ 出现在背景区域, 那么其像素值应该接近每条路径上的最小像素值. 代价函数在此处的值也就相对较小. 这样就可以高亮显著性区域, 暗化背景区域.

Raster Scan 和 FastMBD 算法流程如下图所示.

在论文算法的实现中, 种子集合 $S$ 为 4 个边界处一个像素宽度的行和列. $K$ 为扫描次数. 对一张图像完成这样的一次扫描称为一个 pass, 论文中使用了 3 个 passes, 即 Raster Scan -> Inverse Raster Scan -> Raster Scan, 即 $K=3$.

---

3 Minimum Barrier 显著性目标检测

3.1 Minimum Barrier Distance 显著性目标检测

---

背景种子一般选取图像的边界像素. 使用 Fast-MBD 计算每个颜色通道(彩色图像为 3 个通道)的 MBD 距离图, 然后将所有通道MBD 距离图累加即得到最终的 MBD 距离图, 最后做归一化处理即可.

在 Fast-MBD 中, 路径个数为 3. 这是根据经验值设定的, 当选择更多的路径时, 并不会提高算法的性能.

下图给出了一个用 MBD 和 geodesic distance 获取的显著性图的示例.

可以看出, 对于 geodesic distance 方法, 即使使用自适应边缘权重修剪方法抑制 geodesic distance 方法中存在的小权值累计现象(small-weight-accumulation), 计算得到的显著性图的中心仍然非常模糊. 而MBD 则没有这种问题.

---

3.2 背景边界信息图

---

背景边界信息图的作用是加强显著性图的亮度(即白化显著性图). 显著性图越亮, 使用阈值方法得到的 trimap 就能在图像分割阶段取得很好的前景图. 获取背景边界信息图的具体思路是:

• 选择四个图像边界区域的像素;
• 分别计算图像中所有像素点和 4 个边界区域均值的 Mahalanobis 距离;
• 最终的背景边界信息图是 4 个边界区域求出的背景边界信息之和减去背景边界信息图中的最大值:

$$u^{ij}=\sum _{k=1}^4{u}_k^{ij}-\underset{k}{\max }{u}_k^{ij}\text{\hspace{1em}(8)}$$

最后一步的作用是为了排除某一个边界区域可能包含前景区域时的情况.

将 MB 算法得到的显著性图和背景边界信息图相加可以得到 MB+ 显著性图, 即白化后的 saliency map.

---

4 缺点

---

由于论文中的 MB 算法是基于 Image Boundary Connectify Cue, 因此本算法无法处理显著性目标位于图像边界的情形.

MB 算法中并没有利用像素的位置信息, 导致结果图中相距很远的区域也被高亮, 即被当成是同一个显著性目标.

对于 MB+ 显著性图, 由于其使用背景边界信息对 MB 显著性图进行白化, 因此可以处理前景区域相对于背景区域有较强对比度的情形. 对于前景区域相对于背景区域的对比度较小的情形, MB+ 也不能很好的高亮显著性目标所在的区域.

具体示例如下图所示:

---

参考资料

---

[1]: 项目主页: http://cs-people.bu.edu/jmzhang/fastmbd.html
[2]: Y. Wei, F. Wen, W. Zhu, and J. Sun. Geodesic saliency using background priors. In ECCV. 2012.
[3]: W. Zhu, S. Liang, Y. Wei, and J. Sun. Saliency optimization from robust background detection. In CVPR, 2014.
[4]: B. Jiang, L. Zhang, H. Lu, C. Yang, and M.-H. Yang. Saliency detection via absorbing markov chain. In ICCV, 2013.
[5]: C. Yang, L. Zhang, H. Lu, X. Ruan, and M.-H. Yang. Saliency detection via graph-based manifold ranking. In CVPR. IEEE, 2013.
[6] K. C. Ciesielski, R. Strand, F. Malmberg, and P. K. Saha. Efficient algorithm for finding the exact minimum barrier distance. Computer Vision and Image Understanding, 123:53–64, 2014.
[7]:R. Strand, K. C. Ciesielski, F. Malmberg, and P. K. Saha. The minimum barrier distance. Computer Vision and Image Understanding, 117(4):429–437, 2013.
[8]: R. Strand, K. C. Ciesielski, F. Malmberg, and P. K. Saha. The minimum barrier distance. Computer Vision and Image Understanding, 117(4):429–437, 2013.