非线性方程求解 :二分迭代法和牛顿迭代法
在机器人算法开发中,经常会遇到求解非线性方程。非线性方程的求解十分困难,这里介绍两种方法:
1. 二分法 2.牛顿迭代法
定义:
非线性方程,就是因变量与自变量之间的关系不是线性的关系,这类方程很多,
例如平方关系、对数关系、指数关系、三角函数关系等等.
求解此类方程往往很难得到精确解,经常需要求近似解问题.
二分法:
二分法又称二分区间法,是求解非线性方程的近似根的一种常用的简单方法.
二分法的基本思想是: 首先确定有根区间,将区间二等分, 通过判断f(x)的符号,
逐步将有根区间缩小, 直至有根区间足够地小, 便可求出满足精度要求的近似根。
首先应确定方程在[a,b]区间确定存在至少一个实数根:
由高等数学知识知, 设f (x)为区间[a,b]上的单值连续, 如果f (a)·f (b)<0 ,
则[a,b]中至少有一个实根。如果f (x)在[a,b]上还是单调地递增或递减,
则仅有一个实根.
二分法求根过程
设方程f(x)=0在区间[a,b]内有根,二分法就是逐步收缩有根区间,最后得出所求的根。具体过程如下
① 取有根区间[a,b]之中点, 将它分为两半x0=(a+b)/2,分点,这样就可缩小有根区间
② 对压缩了的有根区间[a1,b1]施行同样的手法,即取中点x1=(a1+b1)/2,
将区间[a1,b1]再分为两半,然后再确定有根区间[a2,b2]],其长度是[a1,b1]的二分之一.
③ 如此反复下去,若不出现f(xk)=0,即可得出一系列有根区间序列,每个区间都是前一个区间的一半,
因此[ak,bk]的长度:
b k − a k = b k − 1 − a k − 1 2 = . . . = b − a 2 k b_k-a_k=\frac{b_{k-1}-a_{k-1}}{2}=...=\frac{b-a}{2^k} bk−ak=2bk−1−ak−1=...=2kb−a
当k->∞时趋于零,区间最终收敛于一点x即为所求的根.
只要二分足够多次,便有:
∣ x ∗ − x k ∣ < ϵ ϵ 是 给 定 的 精 度 , 当 k ≥ l g ( b − a ) − l g ϵ l g 2 − 1 时 , 做 到 k + 1 次 二 分 , 计 算 得 到 的 x k 就 是 满 足 满 足 精 度 的 近 似 解 , 在 程 序 中 通 常 用 相 邻 的 x k 与 x k − 1 的 差 的 绝 对 值 或 a k 与 b k 的 差 的 绝 对 值 是 否 小 于 ε 来 决 定 二 分 区 间 的 次 数 。 |x^*-x_k|<\epsilon \\ \epsilon 是给定的精度,当\\ k \ge\frac{lg(b-a)-lg\epsilon}{lg2}-1时,做到k+1次二分,\\ \\ 计算得到的x_k就是满足满足精度的近似解,在程序中通常用相邻的x_k与x_{k-1}的差的绝对值\\ 或a_k与b_k的差的绝对值是否小于ε来决定二分区间的次数。 ∣x∗−xk∣<ϵϵ是给定的精度,当k≥lg2lg(b−a)−lgϵ−1时,做到k+1次二分,计算得到的xk就是满足满足精度的近似解,在程序中通常用相邻的xk与xk−1的差的绝对值或ak与bk的差的绝对值是否小于ε来决定二分区间的次数。
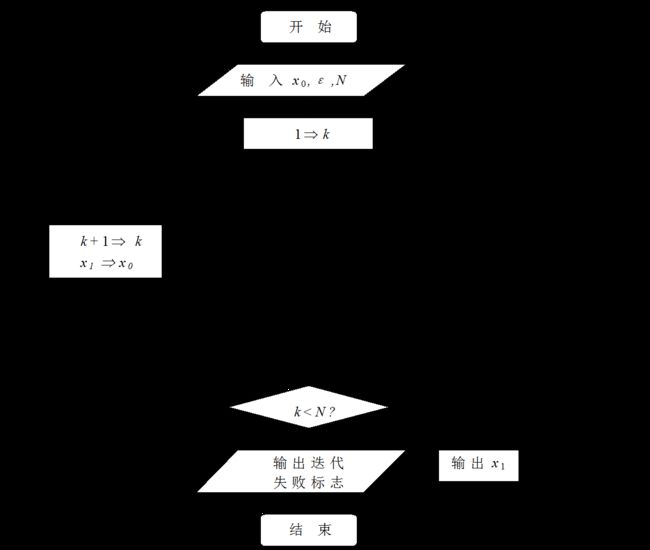
流程图:
牛顿迭代法
牛顿迭代法一种重要和常用的迭代法, 它的基本思想是将非线性函数f(x)逐步线性化, 从而将非线性方程f(x)=0近似地转化为线性方程求解。
牛顿迭代法的推导:
对于方程f(x)=0,设其近似根为xk, 函数f(x)可在xk附近作泰勒展开
f ( x ) = f ( x k ) + f ′ ( x − x k ) + f ′ ′ ( x k ) ( x − x k ) 2 2 + . . . 忽 略 高 次 项 f ( x ) ≈ f ( x k ) + f ′ ( x k ) ( x − x k ) 设 x ∗ 为 实 际 根 , 则 有 f ( x ∗ ) = 0 , 即 x ∗ = x k − f ( x k ) f ′ ( x k ) 这 就 是 牛 顿 迭 代 公 式 : x k + 1 = x k − f ( x k ) f ′ ( x k ) f(x)=f(x_k)+f^{'}(x-x_k)+\frac{f^{''}(x_k)(x-x_k)^2}{2}+...\\ 忽略高次项\\ f(x)≈f(x_k)+f^{'}(x_k)(x-x_k)\\ 设x^*为实际根,则有f(x^*)=0,即\\ x^*=x_k-\frac{f(x_k)}{f^{'}(x_k)}\\ 这就是牛顿迭代公式:\\ x_{k+1}=x_k-\frac{f(x_k)}{f^{'}(x_k)}\\ f(x)=f(xk)+f′(x−xk)+2f′′(xk)(x−xk)2+...忽略高次项f(x)≈f(xk)+f′(xk)(x−xk)设x∗为实际根,则有f(x∗)=0,即x∗=xk−f′(xk)f(xk)这就是牛顿迭代公式:xk+1=xk−f′(xk)f(xk)
流程图:
算法实践
根据S形曲线加减速算法
设置参数条件为:
S = 5.3 V m = 5 V s = 0 V e = 30 A = 100 J = 600 S = 5.3\\ Vm = 5\\ V_s = 0\\ V_e = 30\\ A = 100\\ J = 600\\ S=5.3Vm=5Vs=0Ve=30A=100J=600
推导得知,按照V,J加速到Ve,位移S’>S,即需要降低Ve,解得合适的Ve使得S’=S.
S'计算公式如下:
{ t 1 = A J t 2 = V e − V s A − t 1 S ′ = ( V s + V e ) 2 ∗ ( 2 t 1 + t 2 ) \begin{cases} t1=\frac{A}{J}\\ t_2=\frac{V_e-V_s}{A}-t_1\\ S'=\frac{(V_s+V_e)}{2}*(2t_1+t_2)\\ \end{cases} ⎩⎪⎨⎪⎧t1=JAt2=AVe−Vs−t1S′=2(Vs+Ve)∗(2t1+t2)
使用二分法和牛顿法两种方法迭代计算Ve.
二分法:
核心代码:
//二分法
double a,b;
int n=0;
b = ve;
a = tmp;
while(1){
tmp = (a+b)/2;
n++;
S1 = CalSacc(vs,tmp,A,J);
if(fabs(S1-S)<1e-6){
break;
}
if(S1 > S){
b = tmp;
}
else{
a = tmp;
}
}
共计迭代了n=21次,近似解Ve=25.2738762
牛顿法:
核心代码:
//牛顿法
double a,b,c;
int n=0;
tmp = (tmp+ve)/2;
while(1){
n++;
//ve 在 A*A/J+vs 和 ve之间
a = (vs+tmp)*(A/J+(tmp-vs)/A)-2*S;
b = A/J+(tmp-vs)/A+(vs+tmp)/A;
c = tmp-a/b;
if(fabs(c-tmp)<1e-6){
break;
}
tmp = c;
}