论马尔可夫链的稳定状态与MFC结合在天气预测中的应用
摘要:在《线性代数》课程中学习了“天气马尔可夫链的稳定状态”。马尔可夫模型(HiddenMarkovModel,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来做进一步的分析,例如模式识别。在正常的马尔可夫模型中,状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。而在隐马尔可夫模型中,状态并不是直接可见的,但对于受到状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因此输出符号的序列能够透露出状态序列的一些信息。在这里,我运用计算机科学与技术专业中所用的微软基础类库(英语:Microsoft Foundation Classes,简称MFC),并使用C++语言知识进行编程,深入探究马尔可夫链的稳定状态与MFC结合在天气预测中的应用。
关键字:马尔可夫链;转移概率矩阵;MFC;C++;天气预测。
引言:马尔可夫链模型(Markov Chain Model)是一种常用的概率模型也叫马尔可夫分析(Markov Chain Analysis),其原理为利用概率转移矩阵所进行的模拟分析。此模型为一动态模型,参数可随时间而变,故可以用来预测未来事物变化状态的趋势。
应用案例介绍
该应用案例中,使用ω0三维列向量来存今日晴、阴、雨的概率,
╭0.75, 0.5, 0.25, ╮
转移矩阵A =│ 0.125, 0.25, 0.5, │
╰ 0.125, 0.25, 0.25 ╯
运用公式:ωk = Ak*ω0,k=1,2,3…
即可依次得到第k天的晴、阴、雨天气状态概率,最终得到天气马尔可夫链的稳定状态时的天气状态概率。
在使用MFC编程前,我预先用C语言进行了一个小实验。先用VisualC++6.0新建Win32 Console Aplication的工程编程,定义三维数组w[k][i][j](k=11,i=3,j=1),编写马尔可夫链中矩阵运算,其中“k”表示包括 “今天”在内的从今天起第k天的状态,“i”和“j”表示i行j列的矩阵,定义m_dSunny,m_dCloudy,m_dRainy三个double型变量分别存“晴”、“阴”、“雨”三种天气状态的概率,假设今日天气的三种概率分别为:晴20%,阴30%,雨50%。则先由以下代码简单计算一下未来10天(包括今天)的天气状态概率。
#include
int main()
{
int i, j, k;
double w[11][3][1] = {0.0};
double A[3][3] = {0.75, 0.5, 0.25,
0.125, 0.25, 0.5,
0.125, 0.25, 0.25};
//初始化今日天气:晴20%,阴30%,雨50%。
double m_dSunny = 20, m_dCloudy = 30, m_dRainy= 50;
w[0][0][0] =100*m_dSunny/(m_dSunny+m_dCloudy+m_dRainy);
w[0][1][0] =100*m_dCloudy/(m_dSunny+m_dCloudy+m_dRainy);
w[0][2][0] =100*m_dRainy/(m_dSunny+m_dCloudy+m_dRainy);
for(k = 0; k < 10; k ++) //10天
{
for(i = 0; i < 3; i ++) //行
{
for(j = 0; j < 3; j++) //列
{
w[k+1][i][0] += A[i][j] *w[k][j][0];
}
}
}
for(k = 0; k <= 10; k ++) //10天
{
for(i = 0; i < 3; i ++) //行
{
printf("%d\t", (int)w[k][i][0]);
}
printf("\n\n");
}
return 0;
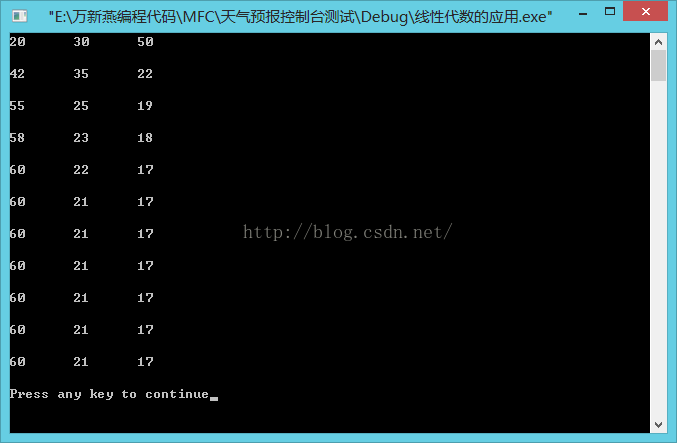
} 控制台窗口打印结果如下:
即包括 “今天”在内的从今天起第k天的状态概率:
这里用的是C语言编写Win32 Console Aplication控制台程序进行的预先实验,可以看到天气状态概率随天数增加逐步趋近于一组常数:晴60%,阴21%,雨17%。即马尔可夫链的稳定状态。
接下来用MFC写对话框程序,部分关键代码如下:
voidCMyDlg::OnButtonSubmit()
{
// TODO: Add your control notificationhandler code here
/***************天气马尔可夫链运算*******************/
//X轴刻度值 0(20, 360)->10(320,360) Y轴刻度值 0(20,360)->10(20, 60) 单位长度30
UpdateData(TRUE);
int i, j, k;
double w[11][3][1] = {0.0}, m;
double A[3][3] = {0.75, 0.5, 0.25,
0.125, 0.25, 0.5,
0.125, 0.25, 0.25};
m = m_dSunny+m_dCloudy+m_dRainy;
w[0][0][0] = 100*m_dSunny/m;
w[0][1][0] = 100*m_dCloudy/m;
w[0][2][0] = 100*m_dRainy/m;
for(k = 0; k < 10; k ++) //10天
{
for(i = 0; i < 3; i ++) //行
{
for(j = 0; j < 3; j++) //列
{
w[k+1][i][0] += A[i][j] *w[k][j][0];
}
}
}
/*************天气马尔可夫链曲线绘制********************/
//Sunny
//强制更新绘图, 不可少, 否则绘图会出错
//使static控件区域无效
pWnd->Invalidate();
//更新窗口
pWnd->UpdateWindow();
CDC *pDC = pWnd->GetDC(); //获取控件的CDC指针
CPen *pPenLine = new CPen(); //创建画笔对象
pPenLine ->CreatePen(PS_SOLID, 3,RGB(255, 255, 0)); //黄色画笔
CPen *pPen = NULL;
//选中当前黄色画笔,并保存以前的画笔
CGdiObject *pOldPen = pDC->SelectObject(pPenLine);
//画线
pDC ->MoveTo(20, 360 - 3 * w[0][0][0]);
for(i = 1; i <=10; i++)
{
pDC ->LineTo(20 + 30 * i, 360 - 3 *w[i][0][0]);
}
//恢复以前的画笔
pDC ->SelectObject(pOldPen);
delete pPenLine;
if(pPen != NULL)
delete pPen;
ReleaseDC(pDC);
//Cloudy
pWnd->Invalidate();
//更新窗口
pWnd->UpdateWindow();
CDC *pDC2 = pWnd->GetDC(); //获取控件的CDC指针
CPen *pPenLine2 = new CPen(); //创建画笔对象
pPenLine2 ->CreatePen(PS_SOLID, 3,RGB(153, 217, 234)); //蓝色画笔
CPen *pPen2 = NULL;
//选中当前蓝色画笔,并保存以前的画笔
CGdiObject *pOldPen2 = pDC->SelectObject(pPenLine2);
//画线
pDC ->MoveTo(20, 360 - 3 * w[0][1][0]);
for(i = 1; i <=10; i++)
{
pDC ->LineTo(20 + 30 * i, 360 - 3 *w[i][1][0]);
}
//恢复以前的画笔
pDC ->SelectObject(pOldPen);
delete pPenLine2;
if(pPen2 != NULL)
delete pPen2;
ReleaseDC(pDC);
//Rainy
pWnd->Invalidate();
//更新窗口
pWnd->UpdateWindow();
CDC *pDC3 = pWnd->GetDC(); //获取控件的CDC指针
CPen *pPenLine3 = new CPen(); //创建画笔对象
pPenLine3 ->CreatePen(PS_SOLID, 3, RGB(0,255, 128)); //绿色画笔
CPen *pPen3 = NULL;
//选中当前绿色画笔,并保存以前的画笔
CGdiObject *pOldPen3 = pDC->SelectObject(pPenLine3);
//画线
pDC ->MoveTo(20, 360 - 3 * w[0][2][0]);
for(i = 1; i <=10; i++)
{
pDC ->LineTo(20 + 30 * i, 360 - 3 *w[i][2][0]);
}
//恢复以前的画笔
pDC ->SelectObject(pOldPen);
delete pPenLine3;
if(pPen3 != NULL)
delete pPen3;
ReleaseDC(pDC);
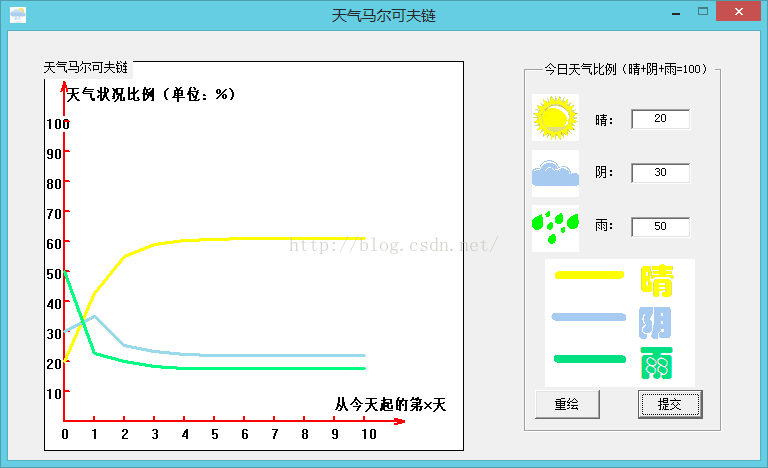
}该函数用于当用户填写好“今日天气比例”后,点击提交按钮时,绘制天气马尔科夫链。
绘制后界面效果如下: