理论： 博弈2： 巴什博奕（Bash Game）

巴什博奕基础情形

只有一堆n个物品，两个人轮流从这堆物品中取物，规定每次至少取一个，最多取m个。最后取光者得胜。

如果n = m + 1； 我们假设第一个人拿走了k个， 还剩下 m + 1 - k。 因为1<=（m + 1 - k）<= m, 所以， 剩下的部分一定可以被第二个人一次性取走。

现在我们将上述规律加一推广：
如果n=（m+1）r+s（r∈ N，s<= m)；
那么先取者要拿走s个物品，如果后取者拿走k（k<= m)个，那么先取者再拿走m+1-k个，结果剩下（m+1）（r-1）个，
以后保持这样的取法，那么先取者肯定获胜

那么在我方取最优解的情况下：
现在我们就发现了巴什博弈的一个必败态： （m + 1）* r （r∈ N）；
那么巴什博弈的必胜态也就可以反推出来： （m + 1）* r + k （1<=k<= m, r ∈N）;

现在我们换一个角度来考虑这个问题：
如果物品数量随机，那么先手一方胜利的概率是m/(m+1)，后手方胜利的概率是1/(m+1)

对于上述的问题， 我们可以用mod的方法快速的求出答案（其实三种博弈的最优美之处就是能用 %^&这三个符号完美解答）


`

巴什博弈演变




硬币问题1

Alice和Bob在玩这样的一个游戏， 给定k个数组a1,a2,a3,……ak。 一开始， 有x枚硬币， Alice和Bob轮流取硬币， 每次所取硬币的枚数硬顶要在 a1,a2,a3,……ak之中。 Alice先取， 取走最后一枚硬币的一方获胜。 当双方都采取最优策略的时候， 谁会获胜？ 题目假定a1,a2,a3,……ak之中一定有1。

下面我们来分情况讨论到达自己时， 还有j枚硬币的胜负情况：

1.题目规定， 取光所有的硬币就获胜， 这等价于轮到自己时如果没有硬币就失败， 因此j = 0时是必败态。
2.如果对于某个i（i<=i<= k）, 就j - ai是必败态， 那么j就是必胜态（如果当前有j枚硬币， 只要取走ai枚对手就必败→自己必胜）；
3.如果对于任意的i（1 <= i <= k）， j - ai都是必败态的话， j就是必败态（无论对手这么走， 对手都必胜， 自己必败）

根据这些规则， 我们都能利用动态规划算法按照j从小到大的顺序计算必胜态。， 只要看x是必胜态还是必败态， 我们就知道谁会取胜；

通常来说， 通过考虑每个小状态的取胜条件， 判断必胜条件和必胜态， 是有胜负的游戏的基础；

上代码

#include
#include
#include

using namespace std;

int x，k;
bool win[100000];
int a[100000];

void Bash()
{//轮到自己没有硬币则必败；
    win[0] = false;

    for (int i = 1; i <= x; i++)
    {//如果可以让对手达到必败态， 则自己必胜；
        win[i] = false;
        for (int j = 0; j < k; i++)
            win[i] |= (a[j] <= i && !win[i - a[j]]); // |=   真真为真 真假为真  假假为假
    }
}

int main(void)
{
    while (scanf("%d %d", &x, &k) != EOF)
    {
        for (int i = 0; i < k; i++)
            scanf("%d", &a[i]);
        sort(a, a + k);
        memset(win, 0, sizeof(a));
        Bash();
        if (win[x])
            printf("Alicce!\n");
        else
            printf("Bob!\n");
    }
    return 0;
}




硬币问题2

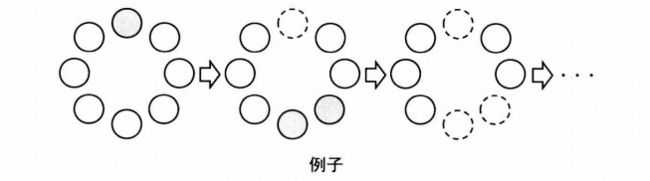
n枚硬币排成一个圈。Alice和Bob轮流从中取一枚或者两枚硬币， 不过， 取两枚时这两枚必须是连续的。硬币取走之后留下空位，想个空位的硬币被认为是不连续。 A开始先取， 取走最后一枚硬币的一方获胜。双方都采取最优策略的时候谁会取胜？

按照上面问题的想法， 我们来拆分一下问题；

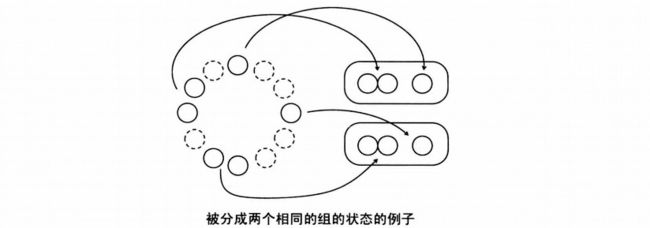
首先我们是想一下如下的情况。 将所有的剩余硬币分成完全相同的组别， 这个是必胜状态还是必败状态？

事实上这是必败态， 无论采取什么策略， 对手只要在另一组中使用相同的策略， 就有回到了相同分组的状态， 而最终的相同分组状态就是（0，0）；

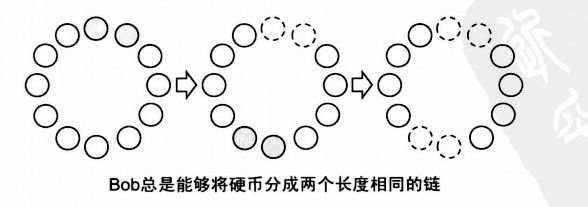
接下来， 我们回归正题。A在第一取走一枚或者两枚硬币之后，称圈的硬币就变成了长度为n - 1或者是n - 2 的。 Bob只要在中间位置根据链的奇偶性， 在链的中间位置取走1或者2枚， 就可以把所有的硬币分成长度相同的两个链。

正如我们所说的，这是必败态， 也就是说， Alice必败， Bob必胜，只不过， 当n <= 2， Alice可以一步取光， 所以胜利的是Alice， 除此之外， 在都进行最优解的情况下， Alice必败。

int k;

if(k <= 2)
    printf("Alice!\n");
else
    printf("Bob\n");




Euclid’s Game(poj 2348)

poj传送门

题目大意：

给定两个整数a, b。Alice和Bob轮流用较大的数减去较小的数的整数倍， 并且相减之后的值不小于0。 如果在自己的回合之内， 相减之后的结果为零， 那么获胜。Alice先手。

根据上述两个问题我们有两个规律可以用上：1.将大问题划分为小问题在进行解决 2.寻找开始（或结束）位置的必败态（或必胜态）在加以正推（或倒推）；

划分： 我们按照后续处理的差别， 将其分为3类：
1.b < a, 我们将a b 进行交换， 使得b恒大于a；
2.a > (b - a)；
3.a < (b - a) ;

对于第一种情况， 为了便于后续处理， 我们将其认为是默认情况；
对于第二种情况， 我么可以选择在b 的基础上减去 a， 或者减去2a和以上；（这一种是有余地的方案）
对于第三种情况， 我们仅仅只有减去a这一种方法；

对于第一种情况：默认的调整方式， 我们用来调整a，b代表的值， 在这里不用讨论（这里实际指的就是swap函数的调用过程）
对于第三种情况， 仅仅只有一种方案： 继续向下迭代， 直到出现最终结局；
对于第二种情况： 假设x是使b - ax < a成立的整数， 那么在第二种情况中又可以分为两种情况 I. b - ax; II.b - a(x - 1);

下面我们讨论 二.I： 这种情况和第三种情况类似， 只能向下迭代， 寻找最终的结果；
对于情况二.II：这种情况的后继情况就是情况就只有b - ax这一种情况， 很巧， 这又回到了情况三。而经过了两次转换， 这种情况依旧是必胜态；

int a, b;

bool flag = true;
while(true)
{
    if(a > b)
        swap(&a, &b);

    if(b % a == 0)
        break;

    if(b - a > a)
        break;

    b -= a;
    flag = !flag; 
}
if(flag)
    printf("Alice!\n");
else
    printf("Bob!\n");