GoGNN: Graph of Graphs Neural Network for Predicting Structured Entity Interactions
论文地址:GoGNN: Graph of Graphs Neural Network for Predicting Structured Entity Interactions
这篇论文被IJCAI 2020接收,主要工作是首次将图神经网络运用在由图构成的图(Graph of Graphs)上。
Graph of Graphs(GoG)
在分化学物质间相互作用的预测任务上,每一个化学物质可以看做是一个图结构,利用图神经网络的方法能够得到化学物质的特征表示,从而预测化学物质间是否存在相互作用。这样的方法只考虑了化学物质内部的图结构信息,而忽视了大量的化学物质及其之间的相互作用本质上也是一个图结构。
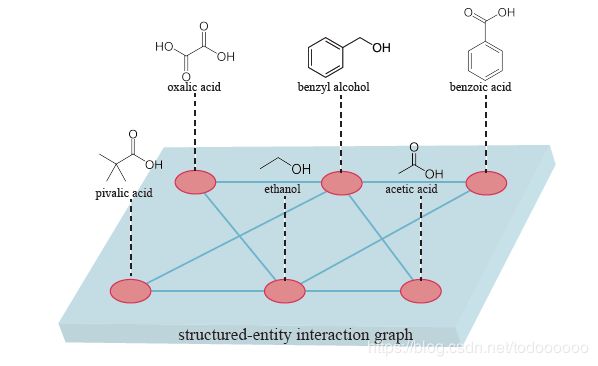
如上图所示,图中的每一个节点也是一个图,所以这是一个由图构成的图(Graph of Graphs)。
Preliminaries
问题定义
本文在两个数据及上做了实验,分别是化学物质相互作用数据集(CCI)和药物相互作用数据集(DDI)。CCI数据集中的相互作用只有一种,DDI中的相互作用有多种,所以在CCI中可通过 ( G i , G j ) \left(G_{i}, G_{j}\right) (Gi,Gj)来计算(i,j)之间存在相互作用的得分 p i j p_{ij} pij,在DDI中通过 ( G i , r , G j ) (G_{i}, r, G_{j}) (Gi,r,Gj)三元组计算(i,j)之间存在关系r的得分 p i j r p_{ij}^{r} pijr。
Molecule Graph
在molecule graph G M G_M GM中,节点 a i {a_i} ai代表原子i,边 e i j e_{ij} eij代表i和j之间的连接。
Interaction Graph
在interaction graph G I = ( N , E I ) G_I=(N, E_I) GI=(N,EI)中, N N N是节点的个数,即 G M G_M GM的数量, E I E_I EI是 G M G_M GM之间的相互作用。
在DDI数据集上,每条边还有一个属性向量 e r e^r er。
GoGNN
基本框架是首先在 G M G_M GM上得到一个表示 x h i d d e n x_{hidden} xhidden,然后再作为 G I G_I GI的输入。
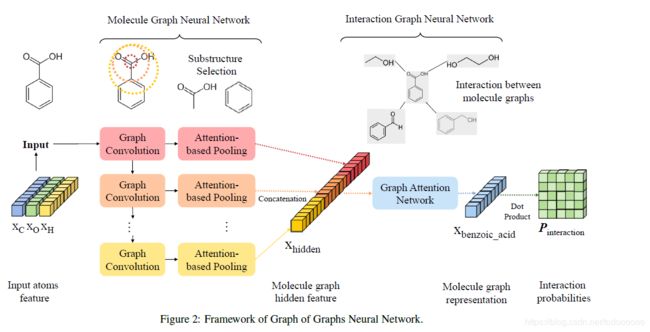
molecule graph neural network
在 G M G_M GM上直接套用GCN:
M ( l + 1 ) = G C N l ( A , M l ) G C N l ( A , M l ) = σ ( D ~ − 1 2 A ~ D ~ − 1 2 M l W l ) \begin{aligned} M_{(l+1)} &=G C N_{l}\left(A, M_{l}\right) \\ G C N_{l}\left(A, M_{l}\right) &=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} M_{l} W_{l}\right) \end{aligned} M(l+1)GCNl(A,Ml)=GCNl(A,Ml)=σ(D~−21A~D~−21MlWl)
为了输出图的表示,在每一层使用self-attention机制,得到 s l ∈ R n × 1 s_{l} \in \mathbb{R}^{n \times 1} sl∈Rn×1
s l = σ ( D ~ − 1 2 A ~ D ~ − 1 2 M l W a t t l ) s_{l}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} M_{l} W_{a t t}^{l}\right) sl=σ(D~−21A~D~−21MlWattl)
where W a t t l ∈ R d × 1 W_{att}^{l} \in \mathbb{R} ^{d \times 1} Wattl∈Rd×1 is the attention weight matrix for the pooling layer to obtain the self-attention score.
挑选出值最高的 ⌈ γ n ⌉ \lceil\gamma n\rceil ⌈γn⌉个维度作为第l层输出的 G M G_M GM的表示:
i d x = top ( s , ⌈ γ n ⌉ ) , s mas k = s i d x M s e l = M ⊙ s m a s k \begin{array}{c} i d x=\operatorname{top}(s,\lceil\gamma n\rceil), s_{\operatorname{mas} k}=s_{i d x} \\ M_{s e l}=M \odot s_{m a s k} \end{array} idx=top(s,⌈γn⌉),smask=sidxMsel=M⊙smask最后将 [ s 1 , s 2 , . . s L ] [s_1, s_2, ..s_L] [s1,s2,..sL]拼接起来即可得到整个 G M G_M GM的表示 x G x_G xG。
interaction graph neural network
Graph Attention Network
在 G I G_I GI上直接套用GAT: x G i l + 1 = ∥ κ = 1 K σ ( ∑ j ∈ η G i α i j κ W κ l x G j l ) \boldsymbol{x}_{G_{i}}^{l+1}=\|_{\kappa=1}^{K} \sigma\left(\sum_{j \in \eta_{G_{i}}} \alpha_{i j}^{\kappa} \boldsymbol{W}_{\kappa}^{l} \boldsymbol{x}_{G_{j}}^{l}\right) xGil+1=∥κ=1Kσ⎝⎛j∈ηGi∑αijκWκlxGjl⎠⎞ α i j = exp ( LeakeyRelu ( a [ W x G i ] ∥ [ W x G j ] ) ) ∑ n ∈ η G i exp ( Leakey Relu ( a [ W x G i ] ∥ [ W x G n ] ) ) \alpha_{i j}=\frac{\exp \left(\operatorname{LeakeyRelu}\left(\boldsymbol{a}\left[\boldsymbol{W} \boldsymbol{x}_{G_{i}}\right] \|\left[\boldsymbol{W} \boldsymbol{x}_{G_{j}}\right]\right)\right)}{\sum_{n \in \eta_{G_{i}}} \exp \left(\operatorname{Leakey} \operatorname{Relu}\left(\boldsymbol{a}\left[\boldsymbol{W} \boldsymbol{x}_{G_{i}}\right] \|\left[\boldsymbol{W} \boldsymbol{x}_{G_{n}}\right]\right)\right)} αij=∑n∈ηGiexp(LeakeyRelu(a[WxGi]∥[WxGn]))exp(LeakeyRelu(a[WxGi]∥[WxGj]))
在计算 α i j \alpha_{ij} αij时论文里的公式没有给出代表是第几层的角标,可能是作者笔误,一般来说每一层 α i j l \alpha_{ij}^{l} αijl应该都是由该层的 x G j l \boldsymbol{x}_{G_{j}}^{l} xGjl和 x G i l \boldsymbol{x}_{G_{i}}^{l} xGil得到。
Edge Aggregation Network
由于DDI数据集上还有边的信息 e i j r e_{ij}^r eijr,所以在聚合时需要将边上的信息考虑进去:

h W e h_{\bold W_e} hWe是一个线性层,所以 h W e ( e i j r ) h_{\bold W_e}({e_{ij}^r}) hWe(eijr)得到的是一个标量。这里作者可能又笔误了,在聚合了邻居节点的信息后没有体现出做线性变换的过程。
Prediction
在CCI数据集上,直接使用 p i j = σ ( x G i T ⋅ x G j ) p_{ij}=\sigma ({\bold x_{G_i} ^T} \cdot {\bold x_{G_j}}) pij=σ(xGiT⋅xGj)得到(i, j)之间的score。在DDI数据集上,需要将特定的关系r考虑进去, p i j r = σ ( ( W r x G i ) T ⋅ ( W r x G j ) ) p_{i j}^{r}=\sigma\left(\left(\boldsymbol{W}_{r} \boldsymbol{x}_{G_{i}}\right)^{T} \cdot\left(\boldsymbol{W}_{r} \boldsymbol{x}_{G_{j}}\right)\right) pijr=σ((WrxGi)T⋅(WrxGj))。