boyu《动手学深度学习Pytorch版》(01) --线性回归，Softmax与分类模型，多层感知机笔记

线性回归

模型公式:
$$\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}=w_{\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}}\cdot \mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}+w_{\mathrm{a}\mathrm{g}\mathrm{e}}\cdot \mathrm{a}\mathrm{g}\mathrm{e}+b$$

• 神经网络中的单个神经元的一部分就是这个公式，只不过在此基础上添加了sigmoid函数

损失函数

$$L(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n{l}^{(i)}(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right)}^2.$$

---

手动实现

w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)

w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

定义变量为tensor

def linreg(X, w, b):
    return torch.mm(X, w) + b

定义模型

def squared_loss(y_hat, y): 
    return (y_hat - y.view(y_hat.size())) ** 2 / 2

损失函数

def sgd(params, lr, batch_size): 
    for param in params:
        param.data -= lr * param.grad / batch_size # ues .data to operate param without gradient track

定义优化迭代函数

# super parameters init
lr = 0.03
num_epochs = 5

net = linreg
loss = squared_loss

# training
for epoch in range(num_epochs):  # training repeats num_epochs times
    # in each epoch, all the samples in dataset will be used once
    
    # X is the feature and y is the label of a batch sample
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y).sum()  
        # calculate the gradient of batch sample loss 
        l.backward()  
        # using small batch random gradient descent to iter model parameters
        sgd([w, b], lr, batch_size)  
        # reset parameter gradient
        w.grad.data.zero_()
        b.grad.data.zero_()
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

训练步骤

使用Pytorch模型来定义网络

class LinearNet(nn.Module):
    def __init__(self, n_feature):
        super(LinearNet, self).__init__()      # call father function to init 
        self.linear = nn.Linear(n_feature, 1)  # function prototype: `torch.nn.Linear(in_features, out_features, bias=True)`

    def forward(self, x):
        y = self.linear(x)
        return y

自定义网络层的经典模板

# method one
net = nn.Sequential(
    nn.Linear(num_inputs, 1)
    # other layers can be added here
    )

# method two
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......

# method three
from collections import OrderedDict
net = nn.Sequential(OrderedDict([
          ('linear', nn.Linear(num_inputs, 1))
          # ......
        ]))

三种组合网络的经典结构

---

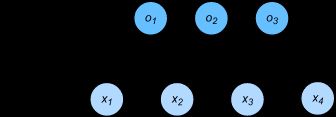
softmax

$o_1,o_2,o_3$分别是三个类别的factor,最后需要转换为概率。

$$\hat{y}1=\frac{\exp (o_1)}{{\sum }_{i=1}^3\exp (o_i)},\hat{y}2=\frac{\exp (o_2)}{{\sum }_{i=1}^3\exp (o_i)},\hat{y}3=\frac{\exp (o_3)}{{\sum }_{i=1}^3\exp (o_i)}.$$

分别表示三种类别的概率

交叉熵损失函数

• 之前用的平方损失不能很好的评价分类结果，例如${\hat{y}}_1^{(i)}={\hat{y}}_2^{(i)}=0.2$比${\hat{y}}_1^{(i)}=0,{\hat{y}}_2^{(i)}=0.4$的损失要小很多，虽然两者都有同样正确的分类预测结果。这主要是因为把误分类的情况也考虑进去了。
• 交叉熵损失函数简化了，只评价正分类的结果。$H({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)})=-\log {\hat{y}}_{y^{(i)}}^{(i)}$。其中${\hat{y}}_{y^{(i)}}^{(i)}$表示模型把输入判定为类别i的概率，而i是ground truth，也就是正确分类的概率。
• 为了矢量化计算方便，交叉熵的公式如下:
  $$H\left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right)=-\sum _{j=1}^q{y}_j^{(i)}\log {\hat{y}}_j^{(i)},$$

多层感知机

• 在线性回归的基础上增加了激活函数，层数
• 经典激活函数有ReLU, sigmoid, tanh

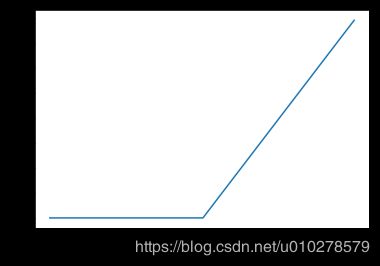
ReLU函数

• 对应的函数导数
  

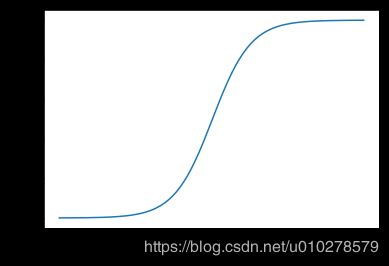
sigmoid 函数

$$\text{sigmoid}(x)=\frac{1}{1+\exp (-x)}.$$

• 对应的函数导数图像
  

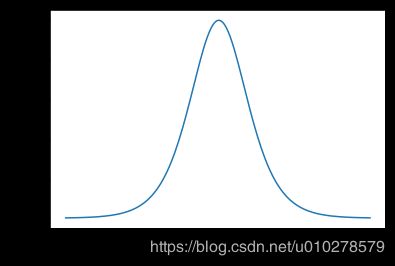
• Sigmoid 的梯度随着结果接近1, -1而急剧减小，意味着在训练的后期会出现“训不动”的现象。相比之下ReLU的梯度一直很稳。对于这个问题Baidu提出过一种方法，在模型训练的而后期，手动增加前面节点的learning rate, 防止update step 淹没。

• tanh函数结构与sigmoid很相似
  $$\text{tanh}(x)=\frac{1-\exp (-2x)}{1+\exp (-2x)}.$$